遗传算法求解TSP问题（python版）

简介

改进和实现遗传算法，用以对旅行商问题(TSP问题)进行建模和近似求解，从而深入对启发式算法的理解。

算法流程

遗传算法解决TSP的流程是以下几部分：初始化种群、计算适应度函数、选择、交叉、变异然后不断重复直到找到理想的解。

模型设定

I 种群初始化。

需要设定的参数是随机生成的初始解的数量，该数量过少会导致种群多样性不足，数量过多会降低算法的效率，我们设定种群规模（初始解数量为150）。

II 适应度函数。

根据数据集说明，其最优解采用的边权重类型为：EDGE_WEIGHT_TYPE : EUC_2D，即两城市之间的距离通过欧式距离计算。

我们得到对路径的所有距离进行求和得到distance，令f=1/distance，即为适应度函数。

III 选择

选择，即在上一代生存的个体中，通过优胜劣汰，使适应性更强的解得以保留。具体而言首先将上一代种群中适应性最强的10%物种保留，然后通过轮盘转赌法，以选择概率为权重，挑出剩下的90%物种。
其中对于每个物种s_i）选择概率计算公式为：

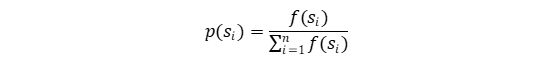
采用上述设定的原因是尽量让适应度更强的物种活下来，同时防止适应性最强的物种因随机性而被轮盘转赌法淘汰。

IV 交叉

通过选择幸存下的物种进行交叉的概率为70%，交叉的方式为单点交叉，即随机选取一个节点，将交叉双方该节点后的部分进行交换。在交换后，单个物种可能会出现有重复城市的情况，因此我们进行了去重操作，即记录下重复的位置，使交叉双方重复的节点进行交换。

V 变异

变异是遗传算法跳出局部最优解的重要操作。在TSP问题中，变异操作是随机选取物种的两个节点，将节点中的城市顺序颠倒。过往的研究表明，变异的概率大于0.5之后，遗传算法将退化为随机搜索。但考虑到跳出局部最优解的重要性，因此我们设定变异的概率为20%。

实验结果

算例一：

(1) 算例名称：DJ38，城市：38，最短距离：6656
来源：http://www.math.uwaterloo.ca/tsp/world/countries.html#DJ

(2) 最优解:
29->28->20->13->9->0->1->3->2->4->5->6->7->8->11->10->18->17->16->15->12->14->19->22->25->24->21->23->27->26->30->35->33->32->37->36->34->31->29

(3) 可视化结果
上部分图片为官方给的路线图，下部分图片为我们求得的最优解。

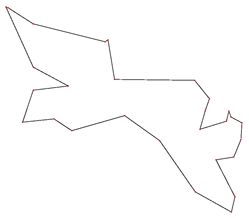
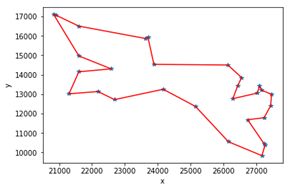
(4) 算法求得的最短距离 随 求解时间 变化结果

(5) 解的质量

Gap=(6659.43 - 6656) / 6656 = 0.05%

算例二

(1) 算例名称：TSPLIB , qa194，城市：194，最短距离：9352
来源：http://www.math.uwaterloo.ca/tsp/world/countries.html#DJ

(2) 最优解路线：
143->149->153->156->163->162->160->155->144->148->145->138->137->141->139->136->133->131->129->126->124->125->113->110->103->100->98->93->97->89->88->81->61->58->35->62->84->85->64->19->0->5->7->15->12->22->24->16->13->10->6->3->1->2->4->8->9->11->14->18->29->31->30->34->37->40->45->43->41->49->48->54->53->51->52->55->47->42->39->33->38->26->36->50->46->57->60->66->72->65->67->63->69->76->83->80->78->82->87->92->95->94->91->96->99->109->111->107->106->104->105->102->90->73->68->59->56->44->28->21->27->32->17->20->23->25->71->77->74->75->70->79->86->101->108->112->118->121->117->130->128->120->116->115->114->119->122->123->127->132->134->142->147->159->165->170->184->192->180->183->187->188->190->191->189->193->181->175->168->171->178->185->186->182->173->172->174->176->177->179->169->161->166->167->164->158->157->154->135->150->146->151->152->140->143

(3) 可视化结果
上部分图片为官方给的路线图，下部分图片为我们求得的最优解。
![在这里插入图片描述](https://img-blog.csdnimg.cn/20201110231636375.png#pic_center

（4）算法求得的最短距离 随 求解时间 变化结果

（5）解的质量

Gap=(10087.017 - 9352) / 9352 = 7.86%

总结

在城市数量较少时，该算法的精度较高，且收敛速度较快。当城市数量多时，算法容易收敛到局部最小值。

实验代码

# -*- coding: utf-8 -*-
"""
Created on Wed Jun  5 18:06:59 2019

@author: 1
"""
#导入需要用到的包
import random
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

#from numba import jit
#初始化参数
species = 200
iters = 5000

def getListMaxNumIndex(num_list,topk=int(0.2*species)):
    '''
    获取列表中最大的前n个数值的位置索引
    '''
    num_dict = {}
    for i in range(len(num_list)):
        num_dict[i] = num_list[i]
    res_list = sorted(num_dict.items(),key=lambda e:e[1])
    max_num_index = [one[0] for one in res_list[::-1][:topk]]
    return max_num_index

#适应度函数
def calfit(trip, num_city):
    total_dis = 0
    for i in range(num_city):
        cur_city = trip[i]
        next_city = trip[i+1] % num_city
        temp_dis = distance[cur_city][next_city]
        total_dis = total_dis + temp_dis    
    return 1 / total_dis

def dis(trip, num_city):
    total_dis = 0
    for i in range(num_city):
        cur_city = trip[i]
        next_city = trip[i+1] % num_city
        temp_dis = distance[cur_city][next_city]
        total_dis = total_dis + temp_dis   
    return total_dis
#交叉函数
def crossover(father,mother):
    num_city = len(father)
    #indexrandom = [i for i in range(int(0.4*cronum),int(0.6*cronum))]
    index_random = [i for i in range(num_city)]
    pos = random.choice(index_random)
    son1 = father[0:pos]
    son2 = mother[0:pos]
    son1.extend(mother[pos:num_city])
    son2.extend(father[pos:num_city])
    
    index_duplicate1 = []
    index_duplicate2 = []
    
    for i in range(pos, num_city):
        for j in range(pos):
            if son1[i] == son1[j]:
                index_duplicate1.append(j)
            if son2[i] == son2[j]:
                index_duplicate2.append(j)
    num_index = len(index_duplicate1)
    for i in range(num_index):
        son1[index_duplicate1[i]], son2[index_duplicate2[i]] = son2[index_duplicate2[i]], son1[index_duplicate1[i]]
    
    return son1,son2

#变异函数
def mutate(sample):
    num_city = len(sample)
    part = np.random.choice(num_city,2,replace=False)
    if part[0] > part[1]:
        max_ = part[0]
        min_ = part[1]
    else:
        max_ = part[1]
        min_ = part[0]
    after_mutate = sample[0:min_]
    temp_mutate = list(reversed(sample[min_:max_]))
    after_mutate.extend(temp_mutate)
    after_mutate.extend(sample[max_:num_city])
    return after_mutate



#读取城市位置数据
import datetime

starttime = datetime.datetime.now()

#long running


df1 = pd.read_csv('size38.txt', sep=' ', header=None)
#df1 = pd.read_csv('size29.txt', sep=' ', header=None)
#df1 = pd.read_csv('size194.txt', sep=' ', header=None)
#df1 = pd.read_csv('size131.txt', sep=' ', header=None)
#df2 = pd.read_csv('st70.txt', sep=' ', header=None)
df1[0] = df1[0] - 1
plot = plt.plot(df1[1], df1[2], '*')

#计算各城市邻接矩阵。
n = len(df1)
distance = np.zeros((n, n))
for i in range(n):
    for j in range(n):
        temp1 = np.power((df1.iloc[i,1] - df1.iloc[j,1]),2)
        temp2 = np.power((df1.iloc[i,2] - df1.iloc[j,2]),2)
        distance[i][j] = np.sqrt(temp1 + temp2)

#初始化种群，生成可能的解的集合
x = []
counter = 0
#for i in range(species):
while counter < species:
    dna = np.random.permutation(range(n)).tolist()
    start = dna[0]
    dna.append(start)
    if dna not in x:
        x.append(dna)
        counter = counter + 1

ctlist = []
dislist = []
ct = 0
while ct < iters: 
    ct = ct + 1    
    f = []
    for i in range(species):    
        f.append(calfit(x[i], n))
    
    
    #计算选择概率
    sig = sum(f)
    p = (f / sig).tolist()
    
    test = getListMaxNumIndex(p)
    testnum = len(test)
    newx = []
    for i in range(testnum):
        newx.append(x[test[i]])
        #newx.append(x[test[i]])
    index = [i for i in range(species)]
    news = random.choices(index,weights=p,k=int(0.8*species))
    newsnum = len(news)
    for i in range(newsnum):
        newx.append(x[news[i]])
        
    m = int(species/2)
    for i in range(0,m):
        j = i + m - 1
        #j=i+1
        numx = len(newx[0])
        if random.choice([1,2,3,4,5,6,7,8,9,10]) < 8:
            tplist1 = newx[i][0:numx-1]
            tplist2 = newx[j][0:numx-1]
            crosslist1,crosslist2 = crossover(tplist1,tplist2)
            if random.choice([1,2,3,4,5,6,7,8,9,10]) < 4:
                crosslist1 = mutate(crosslist1)
                crosslist2 = mutate(crosslist2)
            end1 = crosslist1[0]
            end2 = crosslist2[0]
            crosslist1.append(end1)
            crosslist2.append(end2)
            newx[i] = crosslist1
            newx[j] = crosslist2
    x = newx
    res = []
    for i in range(species):    
        res.append(calfit(x[i], n))  
    result = 1 / max(res)
    res1 = []
    for i in range(species):    
        res1.append(dis(x[i], n))  
    result1 = min(res1)
    print(ct)
    print(result)
    print(result1)
    ctlist.append(ct)
    dislist.append(result)

endtime = datetime.datetime.now()

print (endtime - starttime)

plk1 = []
plk2 = []
for i in range(len(x[0])):
    plk2.append(df1.iloc[x[0][i], 2])
    plk1.append(df1.iloc[x[0][i], 1])
plot = plt.plot(plk1, plk2, c='r')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
    
plot = plt.plot(ctlist, dislist)
plt.xlabel('iters')
plt.ylabel('distance')
plt.show()

需要测试数据请联系博主，或者去我文中提供的来源自行下载。