遗传算法解决TSP
通过遗传算法解决旅行商问题。
旅行商问题,即TSP问题(Traveling Salesman Problem)又译为旅行推销员问题、货郎担问题,是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
算法介绍
遗传算法是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法。它最早由美国密执安大学的Holland教授提出,起源于60年代对自然和人工自适应系统的研究。70年代De Jong基于遗传算法的思想在计算机上进行了大量的纯数值函数优化计算实验。在一系列研究工作的基础上,80年代有Goldberg进行归纳总结,形成了遗传算法的基本框架。
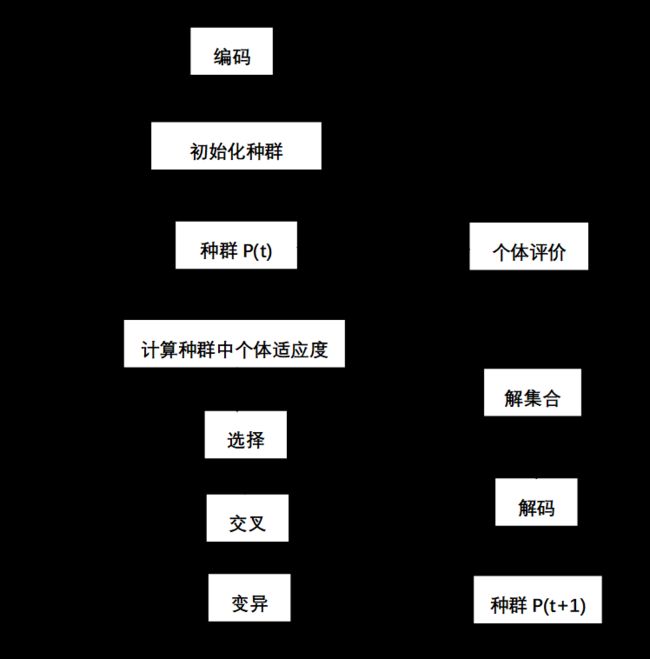
下图所示为遗传算法的运算过程示意图。
由该图可以看出,使用上述三中遗传算子(选择算子,交叉算子,变异算子)的遗传算法的主要运算过程如下所述。
步骤一:编码。将个体变量编码成一种可供运算的符号串。
步骤二:初始化。设置进化代数计数器t=0;设置最大进化代数T;随机生成M个个体作为初始群体P(0).
步骤三:个体评价。计算群体P(t)中各个个体的适应度。
步骤四:选择运算。将选择算子作用于群体。
步骤五:交叉运算。将交叉算子作用于群体。
步骤六:变异运算。将变异算子作用于群体。群体P(t)经过选择、交叉、变异运算之后得到下一代群体P(t+1)。
步骤七:终止条件判断。若t≤T,则:t=t+1,转到步骤二;若t>T,则以进化过程中所得到的具有最大适应度的个体作为最优解输出,终止计算。
运行环境及其实现方法
python 3.9.0 + PyCharm
用到的库:numpy(进行数值计算)、tkinter(GUI库)、matplotlib(2D绘图库)
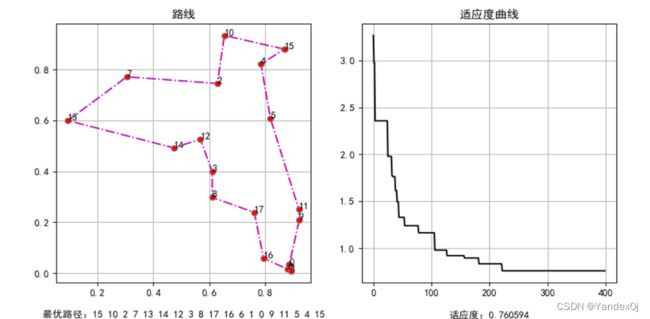
总结果展示及结果分析
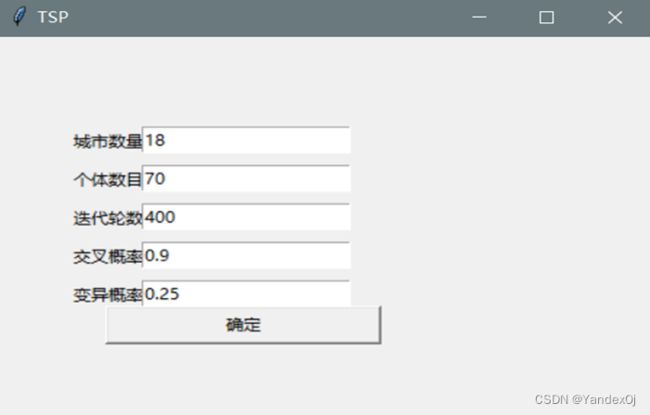
程序包含两个界面,一个是参数输入界面,一个是路线图及适应度曲线展示界面。
首先输入各参数信息,通过城市数量,程序随机初始化城市坐标
城市坐标:
初始状态
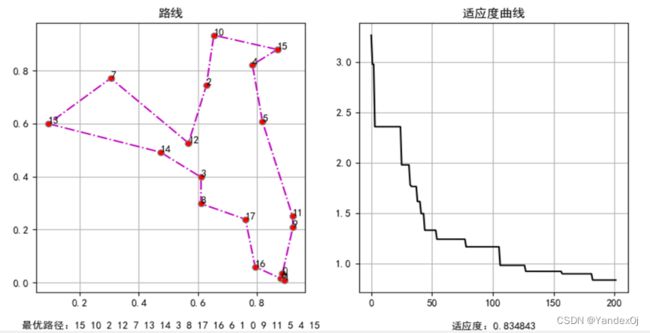
迭代约100次后:
迭代约200次后:
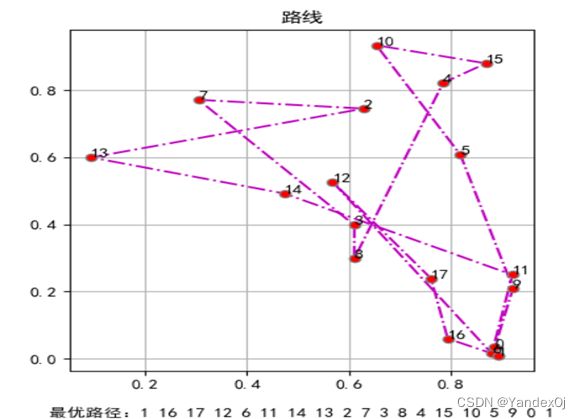
最终结果:
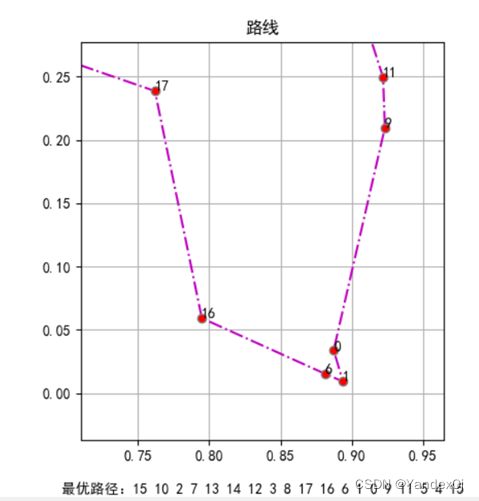
结果局部展示:
图像和适应度曲线实时刷新,当前路径在路线图下方展示,当前适应度在适应度曲线图下方展示。
代码分块展示讲解
程序由main.py和ga.py组成,mian.py是主程序运行文件,ga.py是被调用的算法文件,包括了个体类,和算法类。
main.py:
定义参数,并给予默认值。参数依次是,城市数量、种群中个体数量、迭代轮数、交叉概率、变异概率
返回城市间距离的矩阵
提前将每两个城市之间距离计算至一个list中,方便后续适应度的计算。
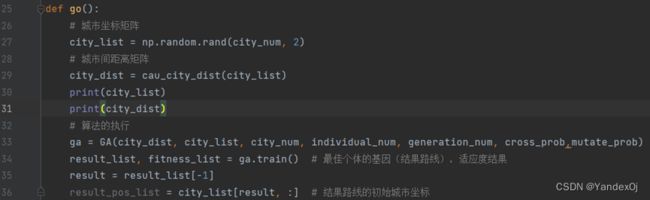
go函数
通过这个函数进入ga.py。通过GA类的构造函数将城市坐标矩阵,城市间距离矩阵,各参数传到ga.py中,从而开始进行遗传算法的运行。
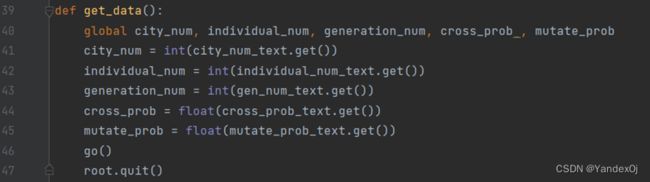
get_data函数
通过此函数接受文本框的输入的各参数值,并调用go函数。
参数数入界面的设计
ga.py
此程序中主要包括三部分。
- 个体类
1.构造函数:
个体类构造函数中包含了个体的编码方式。访问城市的闭环数字序列即是编码方式。若是初始的个体,随机产生序列作为基因,否则将已知序列作为个体基因。
2.计算适应度函数
产生个体的时候,在构造函数里会调用此函数进行适应度的计算。
适应度是通过编码的城市序列和城市间距离矩阵,将相邻序列的距离相加作为个体适度。
- 算法类
1.构造函数
接受参数
![]()
2.交叉运算
因为TSP中要求城市只能访问一次,故采取如下的交叉策略:随机选择种群中的两个个体,再随机选择两个体相同下标的序列片段,通过逐点进行交换。
e.g.:已知两个个体基因,分别是个体1:1 2 3 4 5和个体2:5 4 3 2 1
选取下标为2至3的基因序列片段,即2 3和4 2。首先从下标为2开始:在基因1中找到4,交换2和4,即将4放到下标2的位置,同理在基因2中交换4和2将2放到基因2中下标2的位置。按此规则,依次对基因片段进行交换。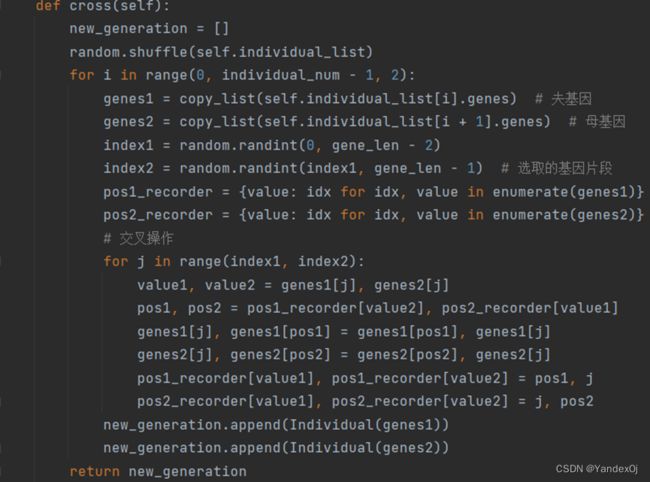
3.变异运算
产生一个0到1之间的随机数,若小于变异概率则进行变异操作。
因为城市的序号是固定的,不能模仿自然界中随机变异,所以采取下面变异方式。
选取个体中一段基因,进行翻转操作,比如选取片段为 2 3 4,则变为4 3 2。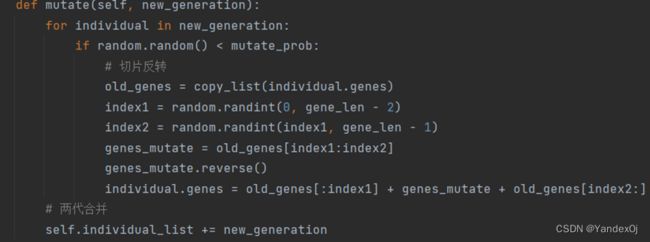
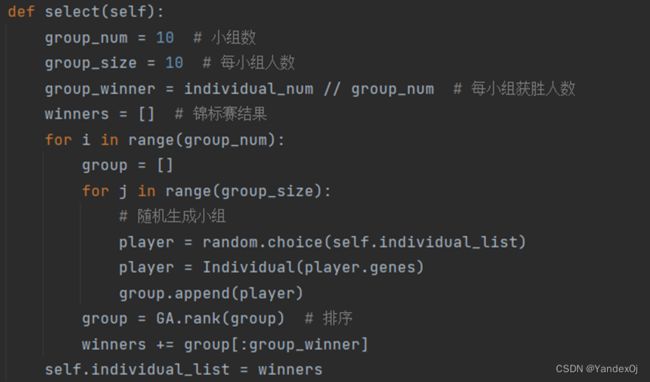
4.选择运算
采用锦标赛算法,总共分成10个小组,每组有individual_num//10个获胜者,最后获得下一代的样本。
5.迭代并作图
根据迭代轮数,每次以种群为单位,进行选择、交叉、变异操作,不断产生新的种群。每次产生新的种群后,计算当代种群中最小的适应度值,将最小适应度值的个体作为当代最优解。
- 绘图
绘图相关代码部分
源代码
main.py
from tkinter import *
import numpy as np
import matplotlib.pyplot as plt
from ga import GA
city_num = 18
individual_num = 70
generation_num = 400
cross_prob = 0.9
mutate_prob = 0.25
# 返回城市间距离的矩阵
def cau_city_dist(in_list):
n = city_num
out_list = np.zeros([n, n])
for i in range(n):
for j in range(i + 1, n):
x = in_list[i, :] - in_list[j, :]
out_list[i, j] = np.dot(x, x)
out_list[j, i] = out_list[i, j]
return out_list
def go():
# 城市坐标矩阵
city_list = np.random.rand(city_num, 2)
# 城市间距离矩阵
city_dist = cau_city_dist(city_list)
print(city_list)
print(city_dist)
# 算法的执行
ga = GA(city_dist, city_list, city_num, individual_num, generation_num, cross_prob,mutate_prob)
result_list, fitness_list = ga.train() # 最佳个体的基因(结果路线),适应度结果
result = result_list[-1]
result_pos_list = city_list[result, :] # 结果路线的初始城市坐标
def get_data():
global city_num, individual_num, generation_num, cross_prob , mutate_prob
city_num = int(city_num_text.get())
individual_num = int(individual_num_text.get())
generation_num = int(gen_num_text.get())
cross_prob = float(cross_prob_text.get())
mutate_prob = float(mutate_prob_text.get())
go()
root.quit()
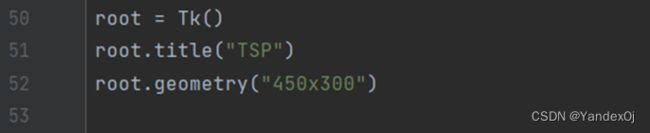
root = Tk()
root.title("TSP")
root.geometry("450x300")
Label(root, text='城市数量:').place(x=50, y=70)
city_num_text = Entry(root)
city_num_text.insert(0, '18')
city_num_text.place(x=100, y=70)
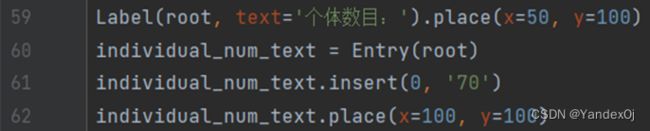
Label(root, text='个体数目:').place(x=50, y=100)
individual_num_text = Entry(root)
individual_num_text.insert(0, '70')
individual_num_text.place(x=100, y=100)
Label(root, text='迭代轮数:').place(x=50, y=130)
gen_num_text = Entry(root)
gen_num_text.insert(0, '400')
gen_num_text.place(x=100, y=130)
Label(root, text='交叉概率:').place(x=50, y=160)
cross_prob_text = Entry(root)
cross_prob_text.insert(0, '0.9')
cross_prob_text.place(x=100, y=160)
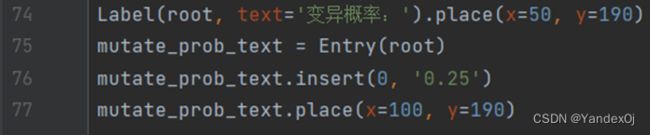
Label(root, text='变异概率:').place(x=50, y=190)
mutate_prob_text = Entry(root)
mutate_prob_text.insert(0, '0.25')
mutate_prob_text.place(x=100, y=190)
Button(root, text='确定', command=get_data).place(x=75, y=210, width=190)
root.mainloop()
ga.py
import random
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
# 绘图
plt.rcParams['font.sans-serif'] = ['SimHei']# 用来设置字体样式以正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
plt.ion() #开启interactive mode 成功的关键函数
fig = plt.figure(figsize=(10,5),edgecolor='black')
gs = gridspec.GridSpec(nrows=1, ncols=2, width_ratios=[1, 1])
city_dist = None
city_list = None
# GA的各元组
gene_len = 18 # 城市数量即基因长度
individual_num = 70 # 每一代中个体数
generation_num = 400 # generation num 迭代轮数
cross_prob = 0.9 # 交叉概率
mutate_prob = 0.25 # 变异概率
# 深拷贝
def copy_list(old_arr: [int]):
new_arr = []
for ele in old_arr:
new_arr.append(ele)
return new_arr
# 种群的个体类,包含基因和适应度
class Individual:
# 构造函数,如果基因为空,则初始化一个1...city_num的基因,然后打乱,代表访问序列
def __init__(self, genes=None):
if genes is None:
genes = [i for i in range(gene_len)]
random.shuffle(genes)
self.genes = genes
self.fitness = self.get_fitness()
# 计算个体的适应度
def get_fitness(self):
fitness = 0.0
for i in range(gene_len - 1):
x = self.genes[i]
y = self.genes[i + 1]
fitness += city_dist[x, y]
fitness += city_dist[self.genes[0], self.genes[-1]] # 将访问路线首位相接
return fitness
# 算法实现类
class GA:
def __init__(self, input_city_dist, input_city_list,a,b,c,d,e):
global gene_len,individual_num,generation_num,mutate_prob
gene_len=a
individual_num=b
generation_num=c
cross_prob=d
mutate_prob=e
global city_dist
global city_list
city_list = input_city_list
city_dist = input_city_dist
self.best = None # 每一代中最佳个体
self.individual_list = [] # 每一代的个体类列表
self.result_list = [] # 每一代对应的解 最佳个体基因
self.fitness_list = [] # 没一代对应的适应度
def cross(self):
new_generation = []
random.shuffle(self.individual_list)
for i in range(0, individual_num - 1, 2):
genes1 = copy_list(self.individual_list[i].genes) # 夫基因
genes2 = copy_list(self.individual_list[i + 1].genes) # 母基因
index1 = random.randint(0, gene_len - 2)
index2 = random.randint(index1, gene_len - 1) # 选取的基因片段
pos1_recorder = {value: idx for idx, value in enumerate(genes1)}
pos2_recorder = {value: idx for idx, value in enumerate(genes2)}
# 交叉操作
for j in range(index1, index2):
value1, value2 = genes1[j], genes2[j]
pos1, pos2 = pos1_recorder[value2], pos2_recorder[value1]
genes1[j], genes1[pos1] = genes1[pos1], genes1[j]
genes2[j], genes2[pos2] = genes2[pos2], genes2[j]
pos1_recorder[value1], pos1_recorder[value2] = pos1, j
pos2_recorder[value1], pos2_recorder[value2] = j, pos2
new_generation.append(Individual(genes1))
new_generation.append(Individual(genes2))
return new_generation
def mutate(self, new_generation):
for individual in new_generation:
if random.random() < mutate_prob:
# 切片反转
old_genes = copy_list(individual.genes)
index1 = random.randint(0, gene_len - 2)
index2 = random.randint(index1, gene_len - 1)
genes_mutate = old_genes[index1:index2]
genes_mutate.reverse()
individual.genes = old_genes[:index1] + genes_mutate + old_genes[index2:]
# 两代合并
self.individual_list += new_generation
def rank(group):
# 冒泡排序
for i in range(1, len(group)):
for j in range(0, len(group) - i):
if group[j].fitness > group[j + 1].fitness:
group[j], group[j + 1] = group[j + 1], group[j]
return group
def select(self):
group_num = 10 # 小组数
group_size = 10 # 每小组人数
group_winner = individual_num // group_num # 每小组获胜人数
winners = [] # 锦标赛结果
for i in range(group_num):
group = []
for j in range(group_size):
# 随机生成小组
player = random.choice(self.individual_list)
player = Individual(player.genes)
group.append(player)
group = GA.rank(group) # 排序
winners += group[:group_winner]
self.individual_list = winners
def train(self):
# 初代种群
self.individual_list = [Individual() for _ in range(individual_num)]
self.best = self.individual_list[0]
# 进行迭代
for i in range(generation_num):
# 获取下一代
new_generation = self.cross() # 交叉
self.mutate(new_generation) # 变异
self.select() # 选择
# 获取这一代的最佳结果
for individual in self.individual_list:
if individual.fitness < self.best.fitness:
self.best = individual
# 将最佳个体基因首尾相连,最为这一代对应的解
result = copy_list(self.best.genes)
result.append(result[0])
plt.clf()
ax0=fig.add_subplot(gs[0,0])
self.result_list.append(result)
now_result = self.result_list[-1]#抽取当前最后一代基因即路线
result_pos_list = city_list[now_result, :]#将当前最优路线传入city_lits获得城市坐标
ax0.plot(result_pos_list[:, 0], result_pos_list[:, 1],'o-.m',markerfacecolor="red",markeredgewidth=1,markeredgecolor="grey")
plt.grid()
plt.title(u"路线")
plt.xlabel("\n最优路径:"+" ".join([str(x) for x in now_result]))
for i in range(len(city_list)):
plt.text(city_list[i,0], city_list[i,1],s='%d'%(i))
ax1=fig.add_subplot(gs[0,1])
self.fitness_list.append(self.best.fitness)
ax1.plot(self.fitness_list,'-k')
plt.grid()
plt.title("适应度曲线")
plt.xlabel("\n适应度:%f" %self.best.fitness)
plt.pause(0.000000001)
plt.ioff()
plt.show()
return self.result_list, self.fitness_list
套的github上的zifeiyu0531用户的,感谢。