人工智能 --- 遗传算法解决TSP问题（JAVA版）

TSP问题，又称旅行商问题、货郎问题。

        问题描述：再给定的城市地图中，要求旅行商走遍所有的城市，且每一个城市只能去一次，求该旅行商能够走遍所有城市的最短路径。

        使用遗传算法解决该问题，遗传算法指通过给定的初始种群，进行有限次的种族迭代，最后使种族中保留个体适应度都是最高的（即适应度高的个体能够再种族中进行繁殖，它们的基因不会被淘汰）,适应度高的个体就代表要求的最优解。

        本文中个体以字符串形式表示，个体集合使用Map population，key：表示个体的染色体，value：表示个体的适应度。使用Map集合是因为能够保证种群中的个体染色体唯一。

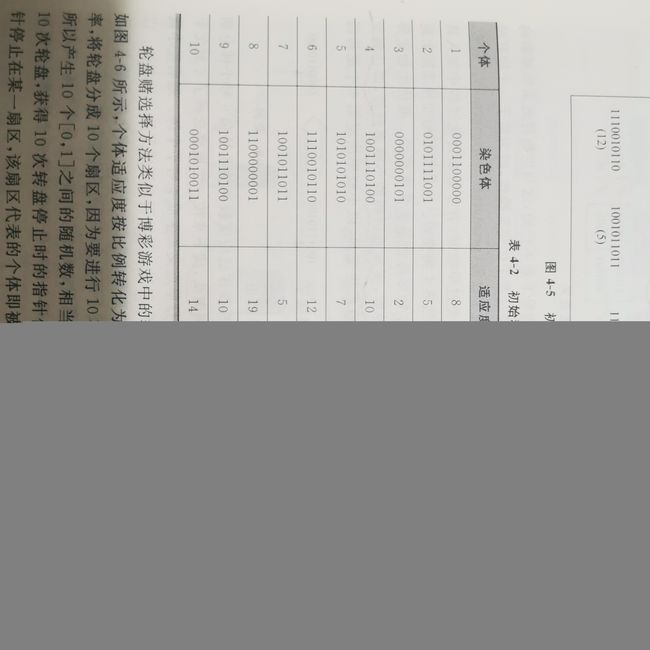
        由上图可以看出，个体适应度值大的个体计算出来的选择概率也就大（选择概率=个体适应度/种群中个体适应度总和），而TSP问题中，个体的优劣是看个体的距离代价是否为最小，因此为了保证距离代价小的个体适应度最大，则定义一个max值（max要足够大，大于距离矩阵中可能出现的最大距离代价的值），个体适应度=max-个体距离代价 。即可保证距离代价小的个体，适应度是大的，最后输出最优解时，在使用max-最优个体适应度，即可算出最小距离代价（最短路径长度）。

在种群迭代的过程中有如下动作:

                random_select(Map population):在种群中随机选择一个符合概率要求的个体（本文中选择根据该方法选出的个体将作为父代进行交叉繁殖出子代）

                reproduce(String x,String y):根据选出的父代个体，进行交叉繁殖，产生一个子代个体

                mutate（String x）：根据随机生成的概率p（random(0~1)），（if p < β）则对传入的个体执行变异操作。变异方法为在个体中随机生成两个坐标，坐标取值范围 1~x.length()-1 此处不能够取下标0 是因为，本文方法中，能够指定起点城市，为了保证后续生成的子代，都是以该城市作为起点城市，所以 在变异函数 mutate 和 交叉函数reproduce 中都要保证不改变 字符串第一位的值。

                select_Best():在种群中选择适应度最大的个体，作为最优个体（best_individual）。

                isRepeat（String x）：判断保证个体的染色体没有重复的基因，在TSP问题中，基因指的就是城市的编号，染色体就是行走方式，而每个城市只能去一次，因此需要保证染色体中没有重复的基因。

*注：本文代码无法保证最后的种群中个体都是最优解个体（解决办法还不会，我是菜鸡），因为种群有个变异函数，及时在某一次迭代过程中，种群只剩一个最优个体后，也会因为变异，而导致个体改变。但是因为只要迭代次数够多，最后都能保证最优解在迭代过程中，出现至少一次，而select_best：将该解保存在了best_individual 中，所以程序最后能输出最优解。若要输出所有最优解，则将best_individual 改成Map 集合，然后对其中的内容进行控制即可。

package com.AI.Experiment4;

import java.util.*;


/**
 * 遗传算法的结点（一个结点作为一个个体）
 */
class GN_Node {
    public String sol;  //存放路径
    public int value;  //存放该路径的距离代价

    public GN_Node(int num){
        sol="";
        value=Integer.MAX_VALUE;
    }
}
/**
 * 遗传算法 解决TSP问题
 *
 *      由于遗传算法要求个体适应度大的易于繁殖，而TSP问题求的是最短路径，
 *      因此需要保证路径值最短的个体的适应度、选择概率、累积概率是相对大
 *      的，因此将个体的适应度 都减去相同的值（该值要足够大。大于所有可
 *      能计算出来的路径长度），再取绝对值。最后的最短路径结果，只需要
 *      使用该值，减去个体的适应度即可。
 */
public class Genetic_algorithms {
    private Map population; //种群,使用map保存个体（individual），key为个体的基因片段，value为个体的评估值，这样可以保证个体的唯一，一个键值对表示一个个体
    private int[][] Dist;   //城市的距离矩阵
    private int city_num;//城市数量
    private float mutate;//个体变异率 （若概率小于该数，则变异个体）
    private int max=3000; //最大值
    private String best_individual; //最优个体
    private int best_distance;  //最短路径长度


    /**
     * 初始化算法执行所需要的各个参数
     * @param dist  城市距离矩阵
     * @param mutate    个体变异率
     * @param start     起点城市
     * @param num       初始化种群大小
     */
    public Genetic_algorithms(int[][] dist,float mutate,int start,int num){
        Dist=dist;
        population=new HashMap<>();
        city_num=Dist.length;
        this.mutate=mutate;
        init(start,num);
    }

    /**
     * 在当前种群中，选出适应度最大的作为最优解
     * @return
     */
    public void select_Best(){
        Set strings = population.keySet();

        for (String string : strings) {
            if(population.get(string)>best_distance){
                best_individual=string;
                best_distance=population.get(string);
            }
        }
    }

    /**
     * 初始化初代种群
     * @param start 起点城市
     * @param num 初代种群大小
     */
    public void init(int start,int num){
        //生成含有10个不相同个体的初始种群
        int i=0;
        Random random=new Random();//用于产生 0~city_num 之间的整数，作为城市编号
       do{
           String individual=""+start;    //个体，保证个体基因不重复，TSP问题中，基因指城市编号

           for(int j=1;j set = population.keySet();
        for (String s : set) {
            sum+=(int)population.get(s);
        }

        for (String s : set) {
            double r=random.nextDouble();   //生成随机选择概率

            //若该个体的选择概率大于随机生成的选择概率，则将该个体作为选择出来的个体进行繁殖
            double value=((double) ((int)population.get(s))/sum);
//            System.out.println(r+","+value+","+(int)population.get(s));
            if(r0&&index new_population=new HashMap<>(); //临时存放新产生的种群

            //每一次迭代，先在种群中选出最优best_individual
            select_Best();

            for(int i=0;i strings = new_population.keySet();
            for (String string : strings) {
                if (!population.containsKey(string)){
                    population.put(string,new_population.get(string));
                }
            }
            System.out.println(population);
            //淘汰部分种群成员，此处淘汰适应度低于平均值的
            Set strings1 = population.keySet();
            int sum=0;
            for (String s : strings1) {
                sum+=population.get(s);
            }

            sum=sum/population.size();

            for (String s : strings1) {         //报错位置！！！！！！！！！！！！！！！！
                if(population.get(s)<=sum){
                    population.remove(s);
                }
            }
            */


            num_iteration++;
            System.out.println("当前迭代第"+num_iteration+"次。种族为："+population);
        }
    }

    public String getBest_individual() {
        return best_individual;
    }

    public int getBest_distance() {
        return best_distance;
    }

    public Map getPopulation() {
        return population;
    }

    public static void main(String[] args) {
        int max=655;

        //距离矩阵
        int[][] Dist={{max,3,2,3,max},{3,max,max,6,4},{2,max,max,1,5},{3,6,1,max,7},{max,4,5,7,max}};
        float a=0.98f;
        Genetic_algorithms sa=new Genetic_algorithms(Dist,a,0,10);

        sa.GN_main();

        System.out.println("最佳行驶路径:"+sa.getBest_individual()+".最短路径:"+(3000-sa.getBest_distance()));
    }
}

广东省各市区之间的距离矩阵：

https://blog.csdn.net/weixin_53068616/article/details/121049943?spm=1001.2014.3001.5501https://blog.csdn.net/weixin_53068616/article/details/121049943?spm=1001.2014.3001.5501

*注:由于广东省有21个市，若要计算该矩阵的最短距离，则需要将字符串改为21进制，即城市编号在个体字符串表现为：0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F、G、H、I、J、K、L。 加多一个函数，将个体字符串，修改回城市编号，然后计算适应度。

        若对本文有任何的疑问或建议欢迎评论区留言。