Python基础-循环练习(数列前n项和、2的n次方、x的y次幂、计算阶乘、阶乘求和、数列求和、奇数列求和、分数序列求和、正负交错数据前n项和、十进制整数转二进制、百钱买百鸡、学生平均成绩与及格人数)
文章目录
- 1. 求数列前n项平方和
- 2. 2的n次方
- 3. 求x的y次幂
- 4. 计算阶乘
- 5. 阶乘求和
- 6. 数列求和
- 7. 奇数数列求和
- 8. 分数序列求和
- 9. 正负交错数列前n项和
- 10. 十进制整数转二进制
- 11. 统计学生平均成绩与及格人数
- 12. 百钱买百鸡
1. 求数列前n项平方和
描述:
现有数列:1,2,3,4,……,n,计算并输出其前n项的平方和,即求:
1×1+2×2+3×3+……+n×n的和。
n = int(input())
sum = 0
for i in range(1,n+1):
sum += i * i
print(sum)
2. 2的n次方
描述:
计算并输出 2 的 n 次方,n 由用户输入 。
输入格式:
输入一个非负整数 n
输出格式:
以整数类型输出2的 n 次方
num = int(input())
print(pow(2, num))
3. 求x的y次幂
描述:
在两行中分别输入x和y两个数,输出x的y次方。
输入格式:
在两行中分别输入x和y两个数
输出格式:
输出x的y次方
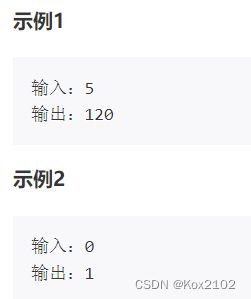
输入输出示例 输入 输出
x = eval(input())
y = eval(input())
print(pow(x, y))
4. 计算阶乘
描述:
用户输入一个非负整数 n,计算并输出其阶乘。
n!=1×2×3×…×n.
输入格式:
输入一个非负整数 n
输出格式:
n 的阶乘
# 解法一
fact = 1
n = int(input())
for i in range(1, n+1):
fact *= i
print(fact)
# 解法二
import math
print(math.factorial(eval(input())))
5. 阶乘求和
描述:
输入一个正整数n,计算 1!+2!+3!+…+n! 的和并输出。
输入格式:
一个正整数n
输出格式:
从1到n每个数的阶乘的和
# 解法一
# 阶乘函数
def factorial(n):
fact = 1
for i in range(1, n+1):
fact *= i
return fact
# 累加函数
def sum_factorial(n):
total = 0
for i in range(1, n+1):
total += factorial(i)
return total
print(sum_factorial(int(input())))
# 解法二
# 计算1!+2!+3!+。。。+n!
def sum_factorial(n):
total, t = 1, 1
for i in range(2, n + 1):
t = t * i
total = total + t
return total
n = int(input())
print(sum_factorial(n))
# 解法三
from math import factorial
print(sum(map(factorial,range(1,n+1))))
6. 数列求和
描述:
用户输入一个小于10的正整数,求1 + 12 + 123 + 1234 + …… 的前n项的和
输入:
一个正整数 n(测试数据保证小于10)
输出:
数列的和
my_sum,temp = 0, 0
n = int(input())
for i in range(1,n + 1):
temp = temp * 10 + i # 每次循环使temp乘10加i
my_sum = my_sum + temp # 累加temp赋值给my_sum
print(my_sum)
7. 奇数数列求和
描述:
输入一个正整数 n,求数列1,3,5,……,(2n-1)的前n项的和。
输入格式:
输入一个正整数 n
输出格式:
数列的和
# 解法一
n = int(input())
sum = 0
for i in range(1,n + 1):
sum = sum + (2 * i - 1)
print(sum)
# 解法二
n = int(input())
print(sum(range(1,2*n,2)))
8. 分数序列求和
描述:
有一分数序列:2/1,3/2,5/3,8/5,13/8,21/13…求出这个数列的前 n 项之和, n 由用户输入。
输入格式:
输入一个正整数
输出格式:
前n项和(保留三位小数)
n = int(input())
sum_of_n = 0
a, b = 2, 1
for i in range(1, n + 1):
sum_of_n = sum_of_n + a / b
b, a = a, a + b
print(round(sum_of_n, 3))
9. 正负交错数列前n项和
描述:
1-1/2+2/3-3/5+4/8-5/13+…的前n项和,n由用户输入(n>0),结果用str.format()方法保留小数点后6位数字输出。
输入格式:
一个正整数
输出格式:
前n项的和
n = int(input())
result = 1 # 首项的值,作为累加初值
sign = -1 # 符号,第二项是负值,
previous, current = 1, 1 # 分母数字的初值,从第二项开始符合这个规律
for i in range(1, n): # 从1到n-1遍历n-1次
previous, current = current, previous + current # 下一个数值是前面两个数的加和
result = result + sign * i / current # 注意分子是 i
sign = -sign # 改变正负号
print('{:.6f}'.format(result))
10. 十进制整数转二进制
描述:
十进制整数转二进制的方法是:除以2,取出余数,商继续除以2,直到得到0为止,将取出的余数逆序即可得到对应的二进制数的各位。
例如:22转二进制的计算过程:
22 / 2 11 余0
11/2 5 余 1
5 /2 2 余 1
2 /2 1 余 0
1 /2 0 余 1
得到22的二进制是10110
输入格式:
输入一个非负整数
输出格式:
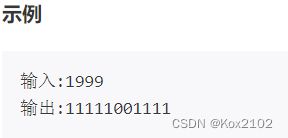
输入一个非负整数
num = int(input())
s=''
if num == 0:
s = '0'
while num != 0:
s = s + str(num % 2) # 将num对2取余的结果转字符串拼接到s
num = num // 2
print(s[::-1])
# 逆序输出字符串
11. 统计学生平均成绩与及格人数
描述:
编写程序,计算学生们的平均成绩,并统计及格(成绩不低于60分)的人数。题目保证输入与输出均在整型范围内。
输出格式:
在一行中给出n个非负整数,即这n位学生的成绩,其间以空格分隔。
输入格式:
按照以下格式输出:
average = 成绩均值 count = 及格人数
score = list(map(int, input().split()))
average = sum(score) / len(score)
count = len(list(x for x in score if x >= 60))
print("average = {}".format(average))
print("count = {}".format(count))
12. 百钱买百鸡
描述:
我国古代数学家张丘建在《算经》一书中提出的数学问题:鸡翁一值钱五,鸡母一值钱三,鸡雏三值钱一。百钱买百鸡,如果要求鸡翁、鸡母、鸡雏都不为零,问鸡翁、鸡母、鸡雏各几何?
输出格式:
每行输出一组结果,按鸡翁数、鸡母数、鸡雏数的顺序输出,数字之间用空格分隔;
如果有多组解时,按鸡翁数量由少到多输出;
for cock in range(1, 101): # 公鸡数量不为0且小于或等于100
for hen in range(1, 101): # 母鸡数量不为0且小于或等于100
for chicken in range(1, 101): # 小鸡数量大于0小于等于100且是3的倍数
if chicken % 3 == 0:
if cock + hen + chicken == 100 and 5 * cock + 3 * hen + chicken // 3 == 100:
print(cock, hen, chicken) # 遇到满足条件的数字组合就输出