Frenet坐标系及其与笛卡尔坐标的转换(1)——原理

目录

1 Frenet坐标系

大多数道路行车场景中的道路走势是笔直的，但弯曲道路仍不少见。道路的弯曲形态多种多样，难以找到统一的曲线类型描述弯曲道路。车辆不应与道路边缘线相撞，这一类碰撞躲避约束的有效建模依赖对于道路布局的精细描述。如何统一简洁地描述道路边缘走势对于轨迹规划问题的求解效率有着重要影响。
与非结构化泊车场景相比，结构化道路场景中存在指引线，车辆行驶轨迹不会大幅度偏离指引线，因此可以考虑以指引线的存在为契机简化规划任务的建模复杂度——构建Frenet坐标系可实现此理念。

2 Frenet坐标系基本概念

在正式介绍 Frenet 坐标系之前，我们认为有必要先做一些基础铺垫。但凡构建一套坐标系即构建一套可用于有效表征空间中各点位置的数据格式。以最基本的笛卡尔坐标系为例，它将平面上每一点的位置向平面内两根相互正交的数轴投影，分别将投影到两条数轴的刻度记录下来，将其整合起来即构成每一点在笛卡尔坐标系中的位置描述，即坐标值。一套理想的坐标系应保证平面内每一点对应且仅对应唯一的坐标值，即坐标值与平面内实际的点位具有一一对应关系，这意味着我们可以放心地使用坐标值代指平面上的点而不会引发理解分歧。

那么，是否还有除笛卡尔坐标系之外的点位描述方式呢？答案是肯定的。假设某人将进村访问某户人家，在没有地图或导航工具辅助的前提下，不得不向他人问路，得到的答复是“沿村口大路向前走，直至遇到三棵大柳树时，右手边距路边十余步的那户人家便是”。在不使用笛卡尔坐标系的条件下，以上描述仍足以精确无误地将某人指引至既定目标点位，那条村中大路和三棵柳树在这里起到了至关重要的作用。 Frenet 坐标系与这种指路模式非常相似，以下将进行详细介绍。

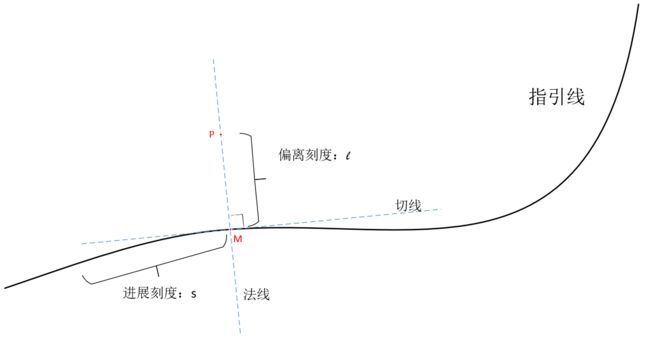
Frenet 坐标系依赖条指引线构建起来，它可以描述平面上一定范围内的点位（稍后介绍其有效表征范围），将每一点用沿指引线延伸方向前行的“进展刻度”与游离于指引线的“编移刻度”表征，分别将两个刻度记录、整合即构成每一点在 Frenet 坐标系中的坐标值。如图下图F1所示，二维平面上每一点 $P$ 在指引线上的投影点 $M$ 能够反映 $P$ 点沿着指引线的进展到度，而 $MP$ 线段长度反映了 $P$ 点游离于指引线的偏移刻度。在上述问路例子中，村中大路代表看指引线， $P$ 点代表目的地， $M$ 点代表路旁三棵柳树。 Frenet 坐标系早在数十年前已应用于车辆轨迹跟踪控制领域开环轨迹被视为指引线，车辆当前位置 $P$ 的进展刻度与闹侈刻度分别用于衡量车辆的纵向、横偏差，据此计算横纵方向上的反馈跟踪控制量。 Weiling 等于2010年首次将 Frenet 坐标系引人结构化道路上的轨迹规划问题中。

图F1：使用Frenet坐标系表示点的方式

在接下来的两小节中介绍笛卡尔坐标系与 Frenet 坐标系之间的转换法，其中第3章节介绍点的转换方法，第4章节介绍运动状态的转换方法 。最后，在第5章节将指出 Frenet 坐标系的局限性。

3 位置：笛卡尔与Frenet坐标点位置的转换

二维平面上的一个点在笛卡尔坐标系中表示为$(x,y)$，也可基于指引线在 Frenet 坐标系中表示为$(s,l)$。本节将介绍如何在给定$(x,y)$的条件下确定$(s,l)$，以及如何在给定$(s,l)$的条件下确定$(x,y)$。

图F2：笛卡尔/Frenet坐标系位置转换模型

3.1 位置：笛卡尔坐标 —> Frenet坐标

首先介绍如何将笛卡尔坐标转化为 Frenet 坐标。已知笛卡尔坐标系下的一段长度为 $L$ 的参数化指引线，将其记为

$$\begin{array}{rl}& \Gamma [x(s),y(s)],s\epsilon [0,L],\end{array}\text{\hspace{1em}(1)}$$

其中， $s$ 为沿着指引线的里程。已知点 $P$ 在笛卡尔坐标系中的坐标为 $(x_e,y_e)$，为了确定 $P$ 在 Frenet 坐标系中的坐标值，需要在曲线段 $\Gamma$ 上寻找与 $P$ 匹配的投影点 $M=(x(s^{\ast }),y(s^{\ast }))$ ，并使线段 $PM$ 长度最短，即

$$\begin{array}{rl}& \underset{s=s^{\ast }}{argmin[D(s)]}\end{array}\text{\hspace{1em}(2)}$$

其中，$D(s)$ 为线段 $PM$ 长度：

$$\begin{array}{rl}& D(s)=[x(s)-x_e{]}^2+[y(s)-y_e{]}^2\end{array}\text{\hspace{1em}(3)}$$

符合条件的 $P$ 点能够使曲线在该点处的切线方向与 $PM$ 方向垂直。如 $PM$ 长度为 $|L^{\ast }|$ ， $M$点位于指引线里程 $s=s^{\ast }$ 处，则 $P$ 在 Frenet 坐标系中的坐标值可确定为 $(s^{\ast },l^{\ast })$ 。不难发现，确定 $M$ 点坐标的关键在于计算 $s^{\ast }$ ，这里提供了两种具体计算方案。

3.1.1 求解 $s^{\ast }$ , $PM$ 长度最短的第一种方法称为二阶最小化方法

第一种方法称为二阶最小化方法，其核心思路是通过多点采样对 $D(s)$ 进行二阶拟合，将拟合而成的二次函数 $D(s)$ 为 $D(s)$ 的估计，随后寻找使 $D(s)$ 取最小值的闭合解。具体而言：

• a 第一步：在曲线上对 $s^{\ast }$ 形成三个不同的初步估算值，分别将其记为 $s_1$ , $s_2$ 以及 $s_3$ 。
• b 第二步：应针对 $D(s)$ 实施二阶拟合，由于此时可以求出 $D(s)$ 在 $s_1$ 、$s_2$ 、 $s_3$ 处的函数值，可据此确定 $D(s)$ 的二阶拟合函数为：
  $$\begin{array}{rl}& D(s)=\frac{(s-s_2)(s-s_3)}{(s_1-s_2)(s_1-s_3)}\cdot D(s_1)+\frac{(s-s_1)(s-s_3)}{(s_2-s_1)(s_2-s_3)}\cdot D(s_2)+\frac{(s-s_1)(s-s_2)}{(s_3-s_1)(s_3-s_{23})}\cdot D(s_3)\end{array}\text{\hspace{1em}(4)}$$
  由于 $D(s)$ 是二次函数，可通过初等数学知识对其求极值 $s$ ：
  $$\begin{array}{rl}& s=\frac{1}{2}\cdot \frac{s{q}_{23}\cdot D(s_1)+s{q}_{13}\cdot D(s_2)+s{q}_{12}\cdot D(s_3)}{er{r}_{23}\cdot D(s_1)+er{r}_{13}\cdot D(s_2)+er{r}_{12}\cdot D(s_3)},er{r}_{ij}=s_i-s_j,s{q}_{ij}=s_i^2-s_j^2\end{array}\text{\hspace{1em}(5)}$$
• c 第三步：需将$s_1$ 、$s_2$ 、 $s_3$ 以及 $s$ 这4个里程数值分别代人 $D(s)$，选取对应函数值较大的3个里程值，将其重新记为$s_1$ 、$s_2$ 、 $s_3$ 并重复第二步，反复执行迭代直至 $s$ 收敛，此时收敛的 $s$ 即为 $s^{\ast }$ 。 $l^{\ast }$ 为区分正负号的变量，其绝对值为 $D(s^{\ast })$ ，如 $P$ 位于指引线延伸方向左侧则取负号，反之取正。至此可确定 $P$ 在 Frenet 坐标系中的坐标值 $(s^{\ast },l^{\ast })$ 。

在工程实践中，通过历史数据提前缩小 $s^{\ast }$ 的可能取值范围，这种做法在曲线里程 $L$ 较大时意义显著。假设限定$s\epsilon [s_k,s_{k+1}]$，则可将 $s^{\ast }$ 的3个初始估计值设置为 $s_k$ 、 $s_{k+1}$ 以及 $(s_k+s_{k+1})/2$ 。若最终 $s^{\ast }$ 收敛至区间 $[s_k,s_{k+1}]$ 之外，则判定选取的区间 $[s_k,s_{k+1}]$ 无效，应在相邻区间中继续进行 $s^{\ast }$ 的迭代求解。

3.1.2 求解 $s^{\ast }$ , 求$PM$ 长度最短的第二种方法称为牛顿法

第二种方法称为牛顿法，其核心思想是以牛顿方法迭代求取使 $D^{{}^{\prime }}(s)=0$ 成立的极值 $s=s^{\ast }$ 。具体地，在提供 $s^{\ast }$ 的某一初始值 $s_{init}$ 后，进行以下迭代：

$$\begin{array}{rl}& s=s_{init}-\frac{D^{\prime }(s_{init})}{D^{\prime \prime }(s_{init})}\end{array}\text{\hspace{1em}(6)}$$

随后使用 $s$ 对 $s_{init}$ 赋值并继续重复计算上式，直至：$s$取值收敛时将收敛值记为$s^{\ast }$ 。

3.1.3 两种方法比较

• 第一种方法收敛速度快（超线性收敛)，但采用二阶拟合会造成求解精度损失；
• 第二种方法因利用 $D(s)$ 二阶导数信息而具有较高求解精度，但收敛速度仅满足二次收敛。
• 在工程实践中可首先利用第一种方法获取粗略解，随后在其微小邻域内采用第二种方法进行精细计算。

3.1.4 求解 $l^{\ast }$

根据求解出的 $s^{\ast }$，代入指引线参数方程，得到点 $P=(x_e,y_e)$ 的投影点（参考点）坐标 $M=(x(s^{\ast }),y(s^{\ast }))$ ，则 $l^{\ast }$ 的绝对值为：
$$|l^{\ast }|=\sqrt{[x_e-x(s^{\ast }){]}^2+[y_e-y(s^{\ast }){]}^2}\text{\hspace{1em}(7)}$$
现在求 $l^{\ast }$ 的正负方向，$P$ 位于指引线延伸方向左侧则取正号，反之取负（一般情况左正右负，看具体定义）。：

在笛卡尔坐标系下，如图F3，根据向量关系，已知向量 $e=OP=\left[\begin{array}{c}{x}_e\\ y_e\end{array}\right]、r=OM=\left[\begin{array}{c}x(s^{\ast })\\ y(s^{\ast })\end{array}\right]$ ，很容易得出：
$$\begin{array}{rl}& e=r+|l^{\ast }|\cdot N_r\\ & e-r=|l^{\ast }|\cdot N_r\\ & \left[\begin{array}{c}{x}_e-x(s^{\ast })\\ y_e-y(s^{\ast })\end{array}\right]=|l^{\ast }|\cdot N_r\\ & N_r=\frac{1}{|l^{\ast }|}\cdot \left[\begin{array}{c}{x}_e-x(s^{\ast })\\ y_e-y(s^{\ast })\end{array}\right],\text{M点处单位法向量}\\ & T_r=\frac{1}{|l^{\ast }|}\cdot \left[\begin{array}{c}{y}_e-y(s^{\ast })\\ -(x_e-x(s^{\ast }))\end{array}\right]=\left[\begin{array}{c}cos{\theta }_r\\ sin{\theta }_r\end{array}\right],\text{M点处单位切向量}\\ & N_r\times T_r=(y_e-y(s^{\ast }))cos{\theta }_r-(x_e-x(s^{\ast }))sin{\theta }_r,\text{叉积在z方向的分量}\end{array}\text{\hspace{1em}(8)}$$

$l^{\ast }$ 的正负号与z分量的符号相同，即:
$$\begin{array}{rl}& l^{\ast }=sign[(y_e-y(s^{\ast }))cos{\theta }_r-(x_e-x(s^{\ast }))sin{\theta }_r]\cdot \sqrt{[x_e-x(s^{\ast }){]}^2+[y_e-y(s^{\ast }){]}^2}\\ & l^{\ast }=std::copysign(\sqrt{[x_e-x(s^{\ast }){]}^2+[y_e-y(s^{\ast }){]}^2},[(y_e-y(s^{\ast }))cos{\theta }_r-(x_e-x(s^{\ast }))sin{\theta }_r])\end{array}\text{\hspace{1em}(9)}$$

3.2 位置：Frenet坐标 —> 笛卡尔坐标

将Frenet 坐标向笛卡尔坐标的转换则相对简单。

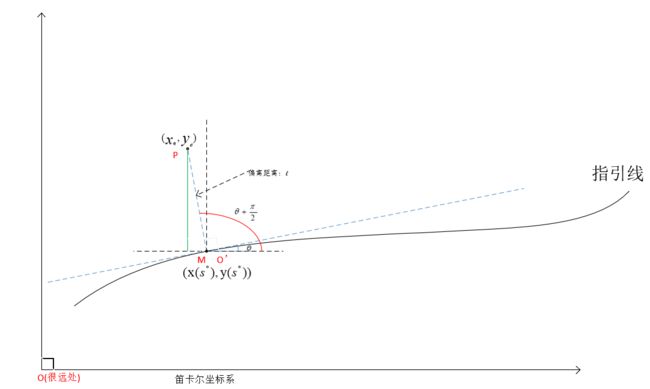
已知一段参数化指引线 $\Gamma [x(s),y(s)]$，以及点 $P$ 在 Frenet 坐标系中的坐标 $(s^{\ast },l^{\ast })$ ，为确定 $P$ 点在笛卡尔坐标系中的坐标值，首先需确定该点在指引线上的投影点 $M=(s^{\ast },0)$ (Frenet坐标下) / $M=(x(s^{\ast }),y(s^{\ast }))$ (笛卡尔坐标下) 处的指引线切线方向 ${\theta }_r$ :

$$\begin{array}{rl}& {\theta }_r=arctan[\frac{y^{\prime }(s^{\ast })}{x^{\prime }(s^{\ast })}]\end{array}\text{\hspace{1em}(10)}$$

随后即可利用几何关系推导出 $P$ 点在笛卡尔坐标系中的坐标值 $(x_e,y_e)$ ：

$$\begin{array}{rl}& (x_e,y_e)\equiv [x(s^{\ast })+l^{\ast }\cdot cos({\theta }_r+\frac{\pi }{2}),y(s^{\ast })+l^{\ast }\cdot sin({\theta }_r+\frac{\pi }{2})]\end{array}\text{\hspace{1em}(11)}$$

4 运动状态：笛卡尔与Frenet坐标点运动状态的转换

前文将平面上一个点在笛卡尔/Frenet 坐标系之间转换。然而，给构化道路上的目标往往存在着运动趋势。例如，社会车辆在笛卡尔坐标系中的未来预测轨迹需要转换至Frenet坐标系中，或是Frenet坐标系中求解的轨迹转换至笛卡尔坐标系中。在对轨迹转换坐标系时倘若仅将轨迹上的一系列采样点按照前文的点位置介绍的方法进行转换，则轨迹原有的速度、加速度等运动状态信息很可能在转换过程中丢失。本小节将探讨如何转换运动状态。

图F3：面向轨迹的笛卡尔/Frenet坐标系运动状态转换模型

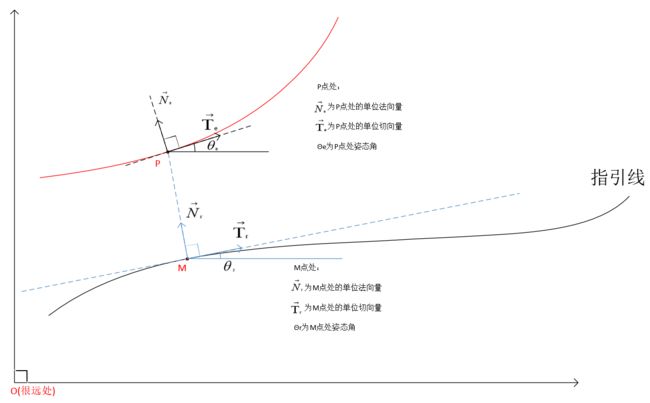
针对图所示的一般情况，我们将介绍轨迹上的某一点 $P$ 的运动状态如何在两个坐标系中相互转换。假设图中存在某一原点 $O$（图中未画出），则向量 $OP$ 体现了点 $P$ 在笛卡尔坐标系下的位置。

$P$ 点在笛卡尔坐标系下的运动状态：(e: Ego)

• 速度 $v_e$
• 加速度 $a_e$
• 姿态角 ${\theta }_e$
• 曲率 $k_e$

$P$ 点在 Frenet 坐标系下的运动状态:

• 坐标 $(s,l)$
• $s(t)$ 的一阶导 $\dot{s}$ ， $\dot{s}=\frac{ds}{dt}$
• $s(t)$的二阶导 $\ddot{s}$ ， $\ddot{s}=\frac{d\dot{s}}{dt}$
• $l(t)$的一阶导 $\dot{l}$ ， $\dot{l}=\frac{dl}{dt}$
• $l(t)$的二阶导 $\ddot{l}$ ， $\ddot{l}=\frac{d\dot{l}}{dt}$
• $l(s)$的一阶导 $l^{\prime }$ ， $l^{\prime }=\frac{dl}{ds}$
• $l(s)$的二阶导 $l^{\prime \prime }$ ， $l^{\prime }=\frac{d{l}^{\prime }}{ds}$

4.1 运动状态：笛卡尔坐标 —> Frenet坐标

**Q:已知笛卡尔坐标系下 $OP、v_e、a_e、{\theta }_e、{\kappa }_e$ 的条件下推导Frenet坐标系下的 $\dot{s}、\ddot{s}、\dot{l}、\ddot{l}、l^{\prime }、l^{\prime \prime }$ 。 **

在已知 $OP$ 条件下，设 $P$ 为 $(x_e,y_e)$ ，可利用3.1小节介绍的方法确定 $(s,l)$ ，以及投影点 $(s,0)$ 处指引线切线与水平线成角 ${\theta }_r$ ，以及该点在指引线上的曲率 ${\kappa }_r(s)=\frac{|y(s{)}^{\prime \prime }x(s{)}^{\prime }-x(s{)}^{\prime \prime }y(s){)}^{\prime }|}{\{[x(s{)}^{\prime }{]}^2+[y(s{)}^{\prime }{]}^2{\}}^{3/2}}$ 。
$$\text{向量相关公式}\{\begin{array}{rl}& OP=\left[\begin{array}{c}{x}_0\\ y_0\end{array}\right],\text{OP向量}\\ & \left|OP\right|=\sqrt{x_0^2+y_0^2},\text{OP向量的模}\\ & OP=\left[\begin{array}{c}\frac{x_0}{\sqrt{x_0^2+y_0^2}}\\ \frac{y_0}{\sqrt{x_0^2+y_0^2}}\end{array}\right],\text{OP向量的单位向量(法向量同向)}\\ & OP=\left[\begin{array}{c}\frac{y_0}{\sqrt{x_0^2+y_0^2}}\\ -\frac{x_0}{\sqrt{x_0^2+y_0^2}}\end{array}\right]=\left[\begin{array}{c}cos\theta \\ sin\theta \end{array}\right],\text{OP向量的单位切向量(与法向量垂直)}\\ & \left|OP\right|=OP\cdot OP\end{array}\text{\hspace{1em}(12)}$$

参数方程的曲线的曲率推导：

参考:曲率、曲率（对弧长）的导数以及曲率导数（对弧长）的导数的计算

参数方程确定的曲线的曲率表达式如何推导？
$$\text{曲率及其一阶导}\{\begin{array}{rl}& \Gamma [x(t),y(t)],t\epsilon [0,L],\text{曲线的参数方程}\\ & \kappa =\frac{d\theta }{ds},\text{曲率定义：角度对弧度的导数}\\ & \frac{dy}{dx}=\frac{dy/dt}{dx/dt}=\frac{y_t^{\prime }}{x_t^{\prime }}=tan\theta ,\text{这里的dt是对应的参数方程中的参数t}\\ & d{s}^2=(dx{)}^2+(dy{)}^2=(x_t^{\prime }\cdot dt{)}^2+(y_t^{\prime }\cdot dt{)}^2=[(x_t^{\prime }{)}^2+(y_t^{\prime }{)}^2]\cdot (dt{)}^2\\ & ds=\sqrt{(x_t^{\prime }{)}^2+(y_t^{\prime }{)}^2}dt,\text{弧微分}\\ & cos\theta =\frac{x_t^{\prime }}{\sqrt{(x_t^{\prime }{)}^2+(y_t^{\prime }{)}^2}}\\ & sin\theta =\frac{y_t^{\prime }}{\sqrt{(x_t^{\prime }{)}^2+(y_t^{\prime }{)}^2}}\\ & se{c}^2\theta =\frac{(x_t^{\prime }{)}^2+(y_t^{\prime }{)}^2}{(x_t^{\prime }{)}^2}\\ & \frac{y_t^{\prime \prime }{x}_t^{\prime }-x_t^{\prime \prime }{y}_t^{\prime }}{x_t^{\prime 2}}=\frac{dtan\theta }{dt}\\ & \kappa =\frac{d\theta }{ds}=\frac{se{c}^2\theta d\theta }{se{c}^2\theta ds}=\frac{dtan\theta }{se{c}^2\theta ds}=\frac{(dtan\theta /dt)}{se{c}^2\theta (ds/dt)}\\ & =\frac{1}{se{c}^2}\cdot \frac{\frac{y_t^{\prime \prime }{x}_t^{\prime }-x_t^{\prime \prime }{y}_t^{\prime }}{x_t^{\prime 2}}}{\sqrt{(x_t^{\prime }{)}^2+(y_t^{\prime }{)}^2}}\\ & =\frac{(x_t^{\prime }{)}^2}{(x_t^{\prime }{)}^2+(y_t^{\prime }{)}^2}\cdot \frac{\frac{y_t^{\prime \prime }{x}_t^{\prime }-x_t^{\prime \prime }{y}_t^{\prime }}{x_t^{\prime 2}}}{\sqrt{(x_t^{\prime }{)}^2+(y_t^{\prime }{)}^2}}\\ & =\frac{y_t^{\prime \prime }{x}_t^{\prime }-x_t^{\prime \prime }{y}_t^{\prime }}{[(x_t^{\prime }{)}^2+(y_t^{\prime }{)}^2{]}^{3/2}}\\ & {\kappa }^{\prime }=\frac{d\kappa }{ds}=\frac{d\kappa }{dt}\frac{dt}{ds}\\ & =\frac{d(\frac{y_t^{\prime \prime }{x}_t^{\prime }-x_t^{\prime \prime }{y}_t^{\prime }}{[(x_t^{\prime }{)}^2+(y_t^{\prime }{)}^2{]}^{3/2}})}{dt}\frac{dt}{ds}\\ & =\frac{(y_t^{\prime \prime }{x}_t^{\prime }-x_t^{\prime \prime }{y}_t^{\prime }{)}^{\prime }[(x_t^{\prime }{)}^2+(y_t^{\prime }{)}^2{]}^{3/2}-(y_t^{\prime \prime }{x}_t^{\prime }-x_t^{\prime \prime }{y}_t^{\prime })([(x_t^{\prime }{)}^2+(y_t^{\prime }{)}^2{]}^{3/2}{)}^{\prime }}{[(x_t^{\prime }{)}^2+(y_t^{\prime }{)}^2{]}^3}\cdot \frac{1}{[(x_t^{\prime }{)}^2+(y_t^{\prime }{)}^2{]}^{1/2}}\\ & =\frac{(y_t^{\prime \prime \prime }{x}_t^{\prime }+y_t^{\prime \prime }{x}_t^{\prime \prime }-x_t^{\prime \prime \prime }{y}_t^{\prime }-x_t^{\prime \prime }{y}_t^{\prime \prime })[(x_t^{\prime }{)}^2+(y_t^{\prime }{)}^2{]}^{3/2}-(y_t^{\prime \prime }{x}_t^{\prime }-x_t^{\prime \prime }{y}_t^{\prime })(\frac{3}{2}[[(x_t^{\prime }{)}^2+(y_t^{\prime }{)}^2{]}^{1/2}](2x_t^{\prime }{x}_t^{\prime \prime }+2y_t^{\prime }{y}_t^{\prime \prime }))}{[(x_t^{\prime }{)}^2+(y_t^{\prime }{)}^2{]}^3}\cdot \frac{1}{[(x_t^{\prime }{)}^2+(y_t^{\prime }{)}^2{]}^{1/2}}\\ & =\frac{[(x_t^{\prime }{)}^2+(y_t^{\prime }{)}^2{]}^{1/2}\{(y_t^{\prime \prime \prime }{x}_t^{\prime }-x_t^{\prime \prime \prime }{y}_t^{\prime })[(x_t^{\prime }{)}^2+(y_t^{\prime }{)}^2]-\frac{3}{2}(y_t^{\prime \prime }{x}_t^{\prime }-x_t^{\prime \prime }{y}_t^{\prime })(2x_t^{\prime }{x}_t^{\prime \prime }+2y_t^{\prime }{y}_t^{\prime \prime })\}}{[(x_t^{\prime }{)}^2+(y_t^{\prime }{)}^2{]}^3}\cdot \frac{1}{[(x_t^{\prime }{)}^2+(y_t^{\prime }{)}^2{]}^{1/2}}\\ & =\frac{(y_t^{\prime \prime \prime }{x}_t^{\prime }-x_t^{\prime \prime \prime }{y}_t^{\prime })[(x_t^{\prime }{)}^2+(y_t^{\prime }{)}^2]-3(y_t^{\prime \prime }{x}_t^{\prime }-x_t^{\prime \prime }{y}_t^{\prime })(x_t^{\prime }{x}_t^{\prime \prime }+y_t^{\prime }{y}_t^{\prime \prime })}{[(x_t^{\prime }{)}^2+(y_t^{\prime }{)}^2{]}^3}\end{array}\text{\hspace{1em}(13)}$$

根据图F3所示的几何关系可得：
$$\begin{array}{rl}& l={MP}^T\cdot N_r=(OP-OM{)}^T\cdot N_r\end{array}\text{\hspace{1em}(14)}$$

其中 $N_r$ 为经过投影点 $M$ 的单位法向量。为叙述简便，现约定了 $e=OP、r=OM$ ，则上式改写为：

$$\begin{array}{rl}& l=(e-r{)}^T\cdot N_r\end{array}\text{\hspace{1em}(15)}$$

4.1.1 推导 $\dot{l}$

首先考虑如何确定 $\dot{l}$ 。将 $l$ 对时间求导可得：(向量位移求导为速度)

$$\begin{array}{rl}\dot{l}& =(\dot{e}-\dot{r}{)}^T\cdot N_r+(e-r{)}^T\cdot \dot{N_r}\\ & =v_e{T_e}^T{N}_r-\dot{s}{T_r}^T{N}_r+l{N_r}^T\dot{N_r}\end{array}\text{\hspace{1em}(16)}$$

其中， $T_e$ 为 $P$ 点处的单位切向量； $T_r$ 为 $M$ 点处的单位切向量。由向量微积分学科中的Frenet-Serret公式可知：

$$\frac{d{N}_r}{ds}=-{\kappa }_r{T}_r\text{\hspace{1em}(17)}$$

这意味着：

$$\dot{N_r}=\frac{d{N}_{r}ds}{dsdt}=-{\kappa }_r{T}_r\dot{s}\text{\hspace{1em}(18)}$$
将公式 $\text{(18)}$ 代入公式 $\text{(16)}$ ，并考虑 ${T_r}^T{N}_r={N_r}^T{T}_r=0$ ，则有：

$$\dot{l}=v_e{T_e}^T{N}_r\text{\hspace{1em}(19)}$$

其中，${T_e}^T{N}_r$ 为两个单位向量 $T_e,N_r$ 的夹角余弦值，即 $cos(\pi /2-{\theta }_e+{\theta }_r)$ ，将其代入公式 $\text{(19)}$ 且令 $\Delta \theta ={\theta }_e-{\theta }_r$ 则有：

$$\dot{l}=v_{e}sin({\theta }_e-{\theta }_r)=v_{e}sin(\Delta \theta )\text{\hspace{1em}(20)}$$

4.1.2 推导 $l^{\prime }$

$$l^{\prime }=\frac{dl}{ds}=\frac{dl}{dt}\frac{dt}{ds}=\frac{v_{e}sin(\Delta \theta )}{\dot{s}}\text{\hspace{1em}(21)}$$

其中分母 $\dot{s}$ 暂时未确定。为了使推导能够进行下去、先聚焦于 $\text{(21)}$ 中的 $v_e$ 部分：

$$v_e=\sqrt{{\dot{e}}^T\dot{e}}\text{\hspace{1em}(22)}$$

其中 $\dot{e}$ 部分有以下关系式：

$$\begin{array}{rl}\dot{e}& =\frac{de}{dt}=\frac{d(r+l{N}_r)}{dt}=\dot{r}+(\dot{l}{N}_r+l\dot{N_r})\\ & =\dot{s}{T}_r+\dot{l}{N}_r-{\kappa }_r\\ & \end{array}$$