二分图匹配-匈牙利算法
二分图概述
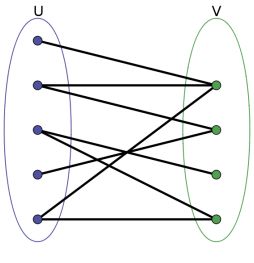
所谓二分图，就是我们可以将图中所有的点分为A、B两个集合，从而使得集合内部任意两个点都不直接相连。
二分图适用于解决一种类似于婚姻匹配的问题，即如果A-B匹配，那么A就不能再和C匹配，即便他们之间有好感。
最大匹配
二分图的最大匹配即需要给出一种分配策略，使得产生尽可能多的对（就是撮合最多多少对情侣）。
匈牙利算法是一个用于解决该类问题的标准算法之一，核心想法是"让路"：假设你（就是红娘）当前想撮合Bi与Gk，但是Gk已经有了对象Bj，此时红娘就和Bj交涉能否让Bj尝试换一个对象，如果Bi能够换一个对象，就可以撮合Bi与Gk；否则撮合失败。
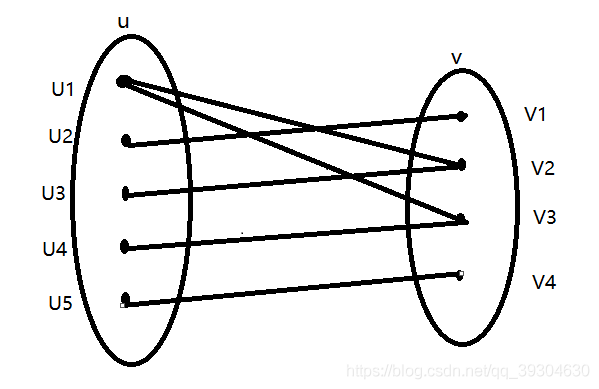
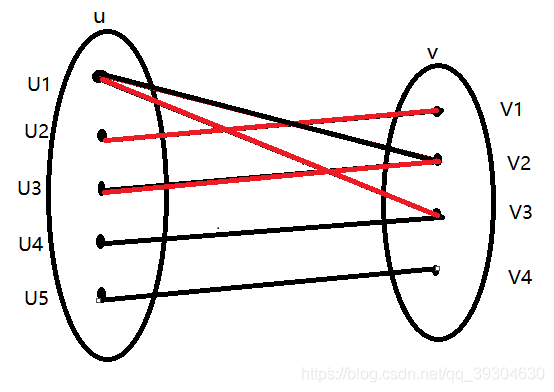
我们来看一个二分图匹配的流程图：
1.首先我们安排u1同学，u1同学与v2同学互有好感，并且v2同学还没有被分配对象，于是撮合u1-v2。
2.现在我们安排u2同学，u2同学对v1有好感，并且v1同学还没有被分配对象，于是撮合u2-v1。
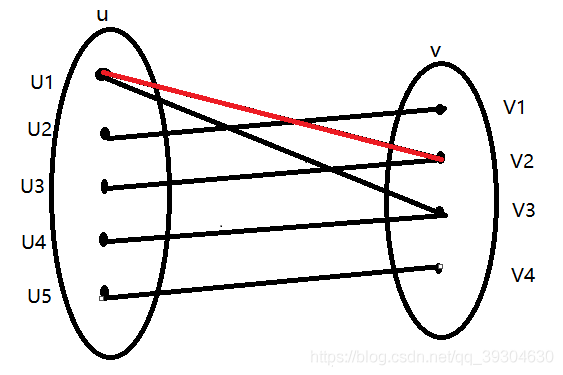
3.现在我们安排u3同学，u3同学对v2有好感，但是v2已经有了对象u1，我们尝试让u1找别人做对象，发现u1还可以可v3做对象，于是断开u1-v2，撮合u1-v3，u3-v2。
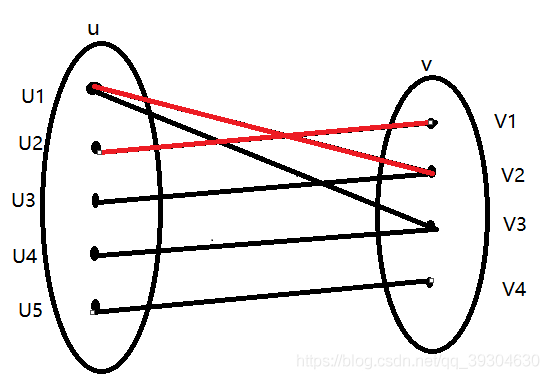
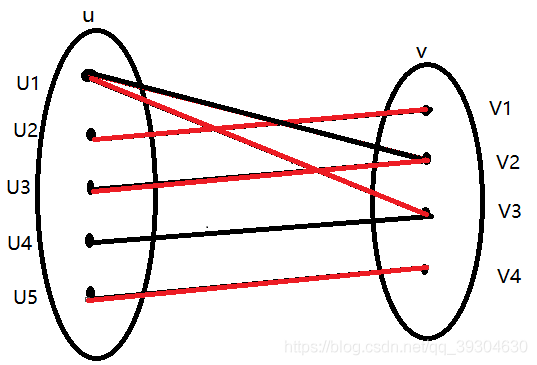
4.现在我们安排u4，u4对v3有好感，但是u1和v3已经是一对了，此时我们想让u1让位，貌似u1还能和v2撮合，但是当我们撮合u1-v2时，u3就会被遗弃，并且由于u3只专情于v2，因此u3就不能和别人撮合到一起了，这真是个悲伤的故事，所以我们决定牺牲掉u4，即u4无法和任何人撮合。(七夕将至，这样不好吧2333）。
5.现在我们安排u5，u5和u4互有好感，并且v4还没有对象，因此直接撮合u5-v4。
综上所述，我们完成了这个二分图匹配过程，最大匹配数为4。
最小点覆盖
即求出最少的点，使得删除包含这些点的边（以这些点作为至少一个端点的的边），可以删除二分图的所有边。这个点的个数与二分图的最大匹配数相等。
代码实现
在实现上，匈牙利算法一般采用DFS的方式：
int N,M; // N:左侧元素个数 M:右侧元素个数
int Map[MaxN][MaxM]; //邻接矩阵
int mate[MaxM]; //右侧元素匹配的对象序号
bool vis[MaxM]; //右侧元素在当前尝试分配的过程中是否被占用
bool match(int i){ //为左侧第i个元素寻找对象
for(int j=1;j<=M;++j){
if(Map[i][j]&&!vis[j]){
vis[j]=true;//想要把j号女生给i号男生
if(mate[j]==0||match(mate[j])){//如果j号女生还没对象或者原对象还有别的选择
mate[j]=i;
return true;
}
}
}
return false;
}
int Hungary(){
int ans=0;
for(int i=1;i<=N;++i){
memset(vis,0,sizeof(vis)); //每一次尝试为一个新人让路的时候，总是优先考虑新人的匹配
if(match(i))++ans;
}
return ans;
}P1129 [ZJOI2007]矩阵游戏
提交9.89k
通过3.96k
时间限制1.00s
内存限制125.00MB
题目描述
小 Q 是一个非常聪明的孩子，除了国际象棋，他还很喜欢玩一个电脑益智游戏――矩阵游戏。矩阵游戏在一个 n \times nn×n 黑白方阵进行（如同国际象棋一般，只是颜色是随意的）。每次可以对该矩阵进行两种操作：
- 行交换操作：选择矩阵的任意两行，交换这两行（即交换对应格子的颜色）。
- 列交换操作：选择矩阵的任意两列，交换这两列（即交换对应格子的颜色）。
游戏的目标，即通过若干次操作，使得方阵的主对角线(左上角到右下角的连线)上的格子均为黑色。
对于某些关卡，小 Q 百思不得其解，以致他开始怀疑这些关卡是不是根本就是无解的！于是小 Q 决定写一个程序来判断这些关卡是否有解。
输入格式
本题单测试点内有多组数据。
第一行包含一个整数 T，表示数据的组数，对于每组数据，输入格式如下：
第一行为一个整数，代表方阵的大小 n。 接下来 n 行，每行 n 个非零即一的整数，代表该方阵。其中 0 表示白色，1 表示黑色。
输出格式
对于每组数据，输出一行一个字符串，若关卡有解则输出 Yes，否则输出 No。
输入输出样例
输入
2
2
0 0
0 1
3
0 0 1
0 1 0
1 0 0
输出
No
Yes思路：其实这题只需要保证有n个黑方块(总的黑方块数可以>n)，两两不在同一行，也不在同一列即可，直接统计每行、每列的元素个数，然后使得个数都保证>=1是无效的，因为会有下面这种情况，符合该条件但不满足两两不同行、两两不同列。
实际上，这种思路可以用DFS+回溯的方式来实现。
#include
using namespace std;
int Col[210],Map[210][210];
inline int read(){
int s=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;
}
bool DFS(int row,int n){
if(row==n+1)return true;
for(int i=1;i<=n;++i){
if(Map[row][i] && !Col[i]){
Col[i]=true;
if(DFS(row+1,n))return true;
Col[i]=false;
}
}
return false;
}
int main(){
int T,n,i,j;
T=read();
while(T--){
n=read();
memset(Col,0,sizeof(Col));
for(i=1;i<=n;++i){
for(j=1;j<=n;++j){
Map[i][j]=read();
}
}
if(DFS(1,n))printf("Yes\n");
else printf("No\n");
}
} 但是回溯法只能过一部分数据(即使经过剪枝)，因为回溯法回溯的时候要回头，而匈牙利算法却是在一直在往前走，因此时间复杂度要优于回溯法。
#include
using namespace std;
int Map[210][210],mate[210];
bool vis[210];
inline int read(){
int s=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;
}
bool match(int i,int n){
for(int j=1;j<=n;++j){
if(Map[i][j] && !vis[j]){
vis[j]=true;
if(!mate[j]||match(mate[j],n)){
mate[j]=i;
return true;
}
}
}
return false;
}
int main(){
int T,n,i,j,count;
T=read();
while(T--){
n=read();
count=0;
memset(mate,0,sizeof(mate));
for(i=1;i<=n;++i){
for(j=1;j<=n;++j){
Map[i][j]=read();
}
}
for(i=1;i<=n;++i){
memset(vis,false,sizeof(vis));
if(match(i,n))++count;
}
printf("%s\n",count==n?"Yes":"No");
}
} Vijos1024 CoVH之柯南开锁
背景
随着时代的演进,困难的刑案也不断增加...
但真相只有一个
虽然变小了,头脑还是一样好,这就是名侦探柯南!
描述
[CoVH06]
面对OIBH组织的嚣张气焰, 柯南决定深入牛棚, 一探虚实.
他经过深思熟虑, 决定从OIBH组织大门进入...........
OIBH组织的大门有一个很神奇的锁.
锁是由M*N个格子组成, 其中某些格子凸起(灰色的格子). 每一次操作可以把某一行或某一列的格子给按下去.
如果柯南能在组织限定的次数内将所有格子都按下去, 那么他就能够进入总部. 但是OIBH组织不是吃素的, 他们的限定次数恰是最少次数.
请您帮助柯南计算出开给定的锁所需的最少次数.
格式
输入格式
第一行 两个不超过100的正整数N, M表示矩阵的长和宽
以下N行 每行M个数 非0即1 1为凸起方格
输出格式
一个整数 所需最少次数
样例1
样例输入1
4 4
0000
0101
0000
0100
样例输出1
2
限制
全部1秒
思路：我们按照上面的逻辑，将凸出方块所在行所在列当作是二分图两个集合中的点，建立连接。那么按下一个凸出方块的动作实际上就是删除这条行-列关系边。而题目中说到每次可以选择一行或者一列按下去。我们知道我们建出来的二分图是行集与列集，因此，选择一行按下，就是删除列集中，与该行有关系的连接。这正好符合了最小点覆盖中，删除与一个点所有有关系的边的条件（因为二分图中，不存在集合内直接联系，因此直接联系只能是跨集合的）。所以这题实际上就是在问最小点覆盖数。
#include
using namespace std;
char Map[1010][1010];
int mate[1010];
bool vis[1010];
bool match(int i,int m){
for(int j=1;j<=m;++j){
if(Map[i][j]=='1' && !vis[j]){
vis[j]=true;
if(!mate[j]||match(mate[j],m)){
mate[j]=i;
return true;
}
}
}
return false;
}
int main(){
int n,m,i,j,count;
cin>>n>>m;
count=0;
for(i=1;i<=n;++i){
cin>>Map[i]+1;
}
for(i=1;i<=n;++i){
memset(vis,false,sizeof(vis));
if(match(i,m))++count;
}
cout< JoyOI 棋盘覆盖 题目链接已经挂了=-=
描述 Description
给出一张n*n(n<=100)的国际象棋棋盘，其中被删除了一些点，问可以使用多少1*2的多米诺骨牌进行掩盖。
输入格式 Input Format
第一行为n，m（表示有m个删除的格子）
第二行到m+1行为x,y，分别表示删除格子所在的位置
x为第x行
y为第y列
输出格式 Output Format
一个数，即最大覆盖格数
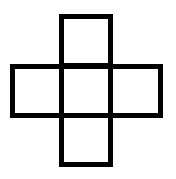
乍一看，这一题可以用搜索来做，但是比较麻烦。有的童鞋可能还想到了状压dp=-=。我们来看二分图匹配如何解决这个问题。首先我们看一下1*2的骨牌能够产生的覆盖方式：
如上图，中心的点为我们当前考察的点，那么可以产生的覆盖方式有如下四种：
我们发现，一个方块，可以和他上下左右四个位置的方块都产生联系，因此我们可以将整个矩阵依据i+j的奇偶性进行分组。下面给出一个3*3矩阵的分组示意：
我们需要将一个方块从坐标转换为它的编号。并且由于本人惯用从1开始的链式前向星存储邻接表，在实现上，必须保证开头的(1,1)对应到编号1。基本的坐标转换公式为
，此处由于存在两个集合，并且匈牙利每次只是重新安排某一边集合的匹配情况。具体来说如下图所示，每次匈牙利运行的时候，只从U出发，考虑U中点的其他匹配；或者从V出发，只考虑V中点的其他匹配，因此我们只需要存储一个集合的点的邻接情况即可。于是我们将上述公式做如下改动：
，同时为了适配本人从点1开始的前向星的存储习惯，所以要保证(1,1)对应到1，因此做调整为
。
代码：
#incllude
using namespace std;
const int MaxN=5010;
int chess[110][110],mate[MaxN],cnt,head[MaxN],vis[MaxN];
//只需要存以左边的点开头的邻接链即可 因为匈牙利每次还是对左边的点重新分配
struct Edge{
int w,next;
};
Edge edges[MaxN*2*4]; //一共MaxN*2个点，每个点有四个连接
int trans(int i,int j,int n){//坐标变数字编号
return ((i-1)*n+j+1)>>1; // (1,1)->1 (1,2)->1
}
void add(int from,int to){ // 存储的邻接表的最小点编号为1
edges[++cnt].to=to;
edge[s].next=head[from];
head[from]=cnt;
}
bool match(int i){
int e,to;
for(e=head[i];e!=0;e=edges[e].next){
to=edges[e].to;
if(!vis[to]){
vis[to]=true;
if(!mate[to] || match(mate[to])){
mate[to]=i;
return true;
}
}
}
return false;
}
int Hungary(int n){
int N=(n*n+1)>>1,ans=0;
for(int i=1;i<=N;++i){//n行n列 坐标转换为编号后，最大的为((n-1)*n+n+1) / 2 = (n*n+1)/2
memset(vis,0,sizeof(vis));
if(match(i))++ans;
}
return ans;
}
int main(){
int n,m,i,x,y;
cin>>n>>m;
for(i=1;i<=m;++i){
cin>>x>>y;
Map[x][y]=-1;//不可使用
}
for(i=0;i<=n+1;++i){
Map[i][0]=Map[0][i]=Map[n+1][i]=Map[i][n+1]=-1;//用边界框包围 可以不用显式考虑边界
}
for(i=1;i<-n;++i){
for(j=1;j<=n;++j){
if(!Map[i][j]){// i j 点需要被覆盖
if(!Map[i-1][j]){// 因为匈牙利算法运行的时候，是从左边考虑新的匹配，因此不必建立从右边到左边的关系边
add(trans(i,j,n),trans(i-1,j,n));
}
if(!Map[i+1][j]){
add(trans(i,j,n),trans(i+1,j,n));
}
if(!Map[i][j-1]){
add(trans(i,j,n),trans(i,j-1,n));
}
if(!Map[i][j+1]){
add(trans(i,j,n),trans(i,j+1,n));
}
}
}
}
cout<