近来做题发现个词 “the maximum cardinality matching” ,不明其意,遂百度一番,无解,只好Google,才找到一个很好的说明。
我把里面的内容摘录下来,只摘录一些名称介绍,剩下的内容进原网站看。
(原文地址:http://www.csie.ntnu.edu.tw/~u91029/Matching.html)
导读
因为 Matching 的算法有点复杂,所以我们同时介绍 Matching 和它的特例 Bipartite Matching 。每当要讲解一个算法时,就先提出 Bipartite Matching 的算法,再进一步提出 Matching 的算法,以循序渐进的方式进行讲解。
Matching
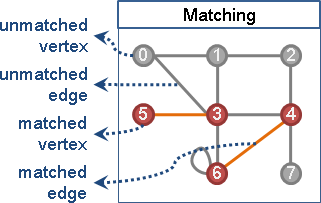
给定一张无向图,当图上两点以边相连时,这两点就可以配成一对──但是呢,一个点最多只能与一个邻点配成一对,宁可孤家寡人,万万不可三妻四妾。双双对对之间的边,整体成为一个「匹配」。
更简单的说法是:令图上各点仅连接着零条边或一条边,这些边构成的集合称做一个「匹配」。
Matched Vertex 与 Unmatched Vertex
一个点要嘛就是和另一个点比翼双飞,要嘛就是孑然一身──前者为「匹配点」,后者为「未匹配点」。
Matched Edge 与 Unmatched Edge
出双入对的两点之间的边为「匹配边」,除此以外则为「未匹配边」。一个匹配是由许多匹配边所组成的。
Cardinality
一个匹配拥有的匹配边数目,也就是配对的数目,称作 Cardinality ,尚无适当中译。
顺便介绍一些特别的匹配:
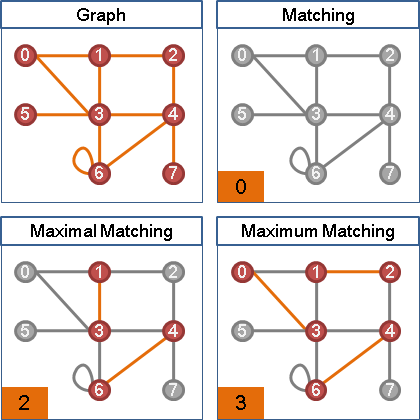
maximal matching: 一张图中,没有办法直接增加配对数的匹配。
maximum matching: 一张图中,配对数最多的匹配。也是maximal matching。
perfect matching: 一张图中,所有点都送作堆的匹配。也是maximum matching。
Weight
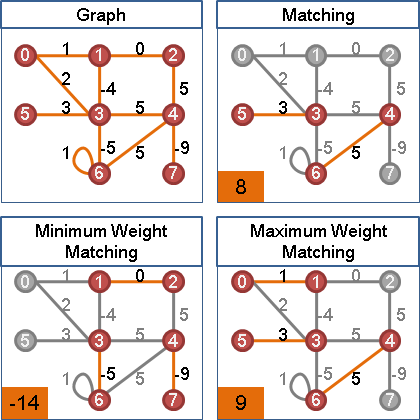
当图上的边都有权重,一个匹配的权重是所有匹配边的权重总和。
顺便介绍一些特别的匹配:
maximum weight matching: 一张图中,权重最大的匹配。
maximum weight maximum cardinality matching:一张图中,配对数最多的前提下,权重最大的匹配。
maximum weight perfect matching: 一张图中,所有点都送作堆的前提下,权重最大的匹配。