强化学习丨多臂老虎机相关算法的总结及其MATLAB仿真
目录
一、前言
二、Bandit问题介绍
三、相关算法介绍及仿真
3.1 ε-贪心算法
3.1.1算法介绍
3.1.2 仿真程序
3.1.3 仿真结果及说明
3.2 非平稳问题
3.2.1 算法介绍
3.2.2 仿真程序
3.2.3 仿真结果及说明
3.3 乐观初始值
3.3.1 算法介绍
3.3.2仿真程序
3.3.3 仿真结果及说明
3.4 无偏恒定步长技巧
3.4.1 算法介绍
3.4.2 仿真程序
3.4.3 仿真结果及说明
3.5 基于置信度上界(upper confidence bound)的动作选择(UCB算法)
3.5.1 算法介绍
3.5.2 仿真程序
3.5.3 仿真结果及说明
3.6 梯度赌博机算法
3.6.1 算法介绍
3.6.2 仿真程序
3.6.3 仿真结果及说明
四、总结
一、前言
前段时间忙于推免的一些琐事,最近总算可静下心来进行下面的学习。结束了Verilog的初步学习(日后还会更新一则脉压的仿真设计和上板实操),在老师的指导与推荐下,笔者开始攻读《强化学习》([著]Richard S.Sutton,Andrew G.Barto [译]俞凯)一书,之后有条件的话也会更新相关的仿真与总结,与诸君共同讨论学习。
二、Bandit问题介绍
在强化学习的任务中,我们总会遇到开发与试探的权衡问题:
开发:智能体选择在过去对其产生过效益的动作,即开发已有的经验来获取收益。
试探:智能体尝试经验所认知的最优动作外的其它动作,以此来获得更好的选择空间。
根据两者定义可以看出两者之间存在的制衡与矛盾。 而在强化学习领域就有一个问题很清晰的反映了两者之间的这种对立统一的关系——多臂老虎机问题(Bandit),问题介绍如下:
假设你面前有一台赌博机(老虎机),这台机器上有k个不同的操纵杆,每一次动作选择就是拉动老虎机的一个操纵杆,而收益就是得到的奖金。通过多次的重复动作选择,你要学会将动作集中到最好的控制杆上,从而最大化你的奖金。
三、相关算法介绍及仿真
为了定量对比算法的优劣,引入全局平均收益与全局最优动作比率作为对比的指标,定义如下:
全局平均收益(Average Reward):在每次学习过程(可以理解为对多个不同的老虎机同时进行训练)的相同训练步数下的平均收益的平均值(注意:这里有两个“平均”)。例如对于第m次学习过程,在第n次训练步数下可以得到前n次的实际收益的平均值
,而对于LearnN次学习过程而言,则是将LearnN次在第n步的
进行加和平均,从而得到全局平均收益。
全局最优动作比率(Optimal Action Rate):同上,即在第m次学习过程,在第n次训练步数下可以得到前n次中选择最优动作次数的比率,再对LearnN次学习过程进行加权平均。
3.1 ε-贪心算法
3.1.1算法介绍
对于该问题,最容易想到的方法就是:先试验几次,此后根据之前的赌博机反馈都选择收益期望(价值)最大的杆(动作)。其中每次动作前每个臂杆的价值是通过实际收益的平均值来估计的:
而t时刻的动作选择可用以下方式来表示:
![]()
这就是最基础的贪心算法,即忽略试探,过度强调开发,但这真的是最优解吗?即这真的可以得到最大的收益吗?
为了对比,不妨给予智能体一定的试探概率,即对于每次的动作选择,智能体都有ε(0<ε<1)的概率等概率选择经验中价值最高的动作之外的其它动作,这也就是ε-贪心算法。
3.1.2 仿真程序
本仿真任务中老虎机的基本参数如下:
臂杆数:10;
学习次数:2000;
每次学习的训练步数:1000;
10个臂杆的收益期望服从单位正态分布;
每次动作的收益服从以选择臂杆的收益期望为均值,方差为1的正态分布。
需要说明的是, Bandit的相关算法中存在许多求平均值的地方(如![]() 值、全局平均收益以及全局最优动作比率的迭代),而若将所有的对象先存储起来在平均就会消耗大量的存储资源。对此,可采用增量式的方式进行加权求和(将求和项里的前n-1项拆分出来即可证明),此处给出
值、全局平均收益以及全局最优动作比率的迭代),而若将所有的对象先存储起来在平均就会消耗大量的存储资源。对此,可采用增量式的方式进行加权求和(将求和项里的前n-1项拆分出来即可证明),此处给出![]() 值的迭代公式如下:
值的迭代公式如下:
其余求平均可参上式。
先给出MATLAB仿真代码如下,各个参数定义与算法过程详见注释:
%% 参数初始化
clc,clear;
ArmN = 10; %老虎机臂(可选动作)数
Epsilon = [0 0.01 0.1];%用以随机探索其它杆臂的可能性
TrialN = 1000; %每次学习的实验次数(训练步数)
LearnN = 2000; %总学习次数
Range = 1:TrialN; %1-1000递增序列
%% 训练过程
for epsilon = Epsilon
reward_total_set = zeros(1,TrialN); %存放全局总平均收益的数组
reward_set = zeros(1,TrialN); %存放单次训练平均收益的数组
OpAction_set = zeros(1,TrialN); %存放单次训练最优动作比率的数组
OpAction_total_set = zeros(1,TrialN);%存放全局最优动作比率的数组
for m = 1:LearnN
Value = randn([1 ArmN]); %根据单位正态分布产生各动作的收益期望
OpAction = 0; %最优动作比率初始化
reward_total = 0; %平均收益
[Value_max,Value_max_a] = max(Value);%选出最优动作
Q = zeros(1,ArmN); %各动作估计收益初始化
N = zeros(1,ArmN); %各动作选择次数初始化
for n = 1:TrialN %开始单次学习训练
[Qmax,i] = max(Q); %根据估计收益选出最优收益和最优动作
if(Qmax~=0 && rand(1)<1-epsilon) %根据epsilon选择是否随机选择动作(至于Qmax~=0——与其选择印象里没有收益的动作,倒不如随机选择赌一波)
action = i; %以1-epsilon的概率选择贪婪动作
else
action = unidrnd(ArmN); %以epsilon随机选择动作
end
reward = normrnd(Value(action),1); %以均值为Value(action)、方差为1的正态分布产生实际收益
N(action) = N(action) + 1; %选择动作的次数自加一
Q(action) = Q(action) + (1/N(action)) * (reward - Q(action));%根据选择动作的估计收益
reward_total = reward_total + 1/n * (reward-reward_total); %更新平均收益
reward_set(n) = reward_total; %填充平均收益数组
if (i==Value_max_a) %判断是否为最优动作
OpAction = OpAction + 1;
end
OpAction_set(n) = OpAction; %填充最优动作次数数组
end
reward_total_set = reward_total_set + 1/m * (reward_set - reward_total_set); %更新全局平均收益数组
OpAction_total_set = OpAction_total_set + 1/m * (OpAction_set - OpAction_total_set);%更新最优动作次数数组
end
%绘制全局平均收益随训练步数变化的图线
figure(1);
plot(reward_total_set);
hold on;
legend('Greedy','Epsilon=0.01','Epsilon=0.1');
xlabel('训练步数');ylabel('平均收益');
%绘制最优动作比率随训练步数变化的图线
figure(2);
OpAction_total_set = OpAction_total_set ./ Range;%将次数化为比率
plot(OpAction_total_set);
hold on;
legend('Greedy','Epsilon=0.01','Epsilon=0.1');
xlabel('训练步数');ylabel('最优动作');
end3.1.3 仿真结果及说明
通过运行程序可得到仿真结果如下:
可以看到,贪心算法在最初增长的稍微快些,但是随后便稳定在一个较低的水平。从长远来看,贪心的方法表现的更糟,因为它经常陷入执行次优的动作的怪圈;而下部的图也显示出贪心算法大约只有三分之一的任务中找到了最优动作,在另外三分之二的动作中,最初采样得到的动作非常不好,因此贪心算法无法跳出找到最优动作。
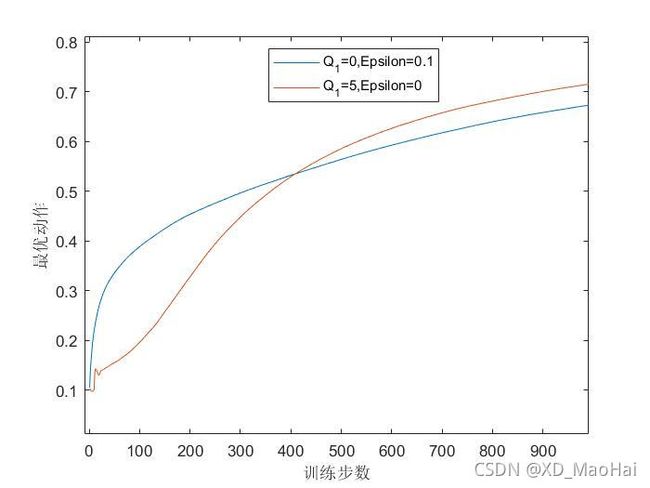
相比之下,ε-贪心算法则表现的更好,因为他们持续的试探并且找到最优动作的机会。ε=0.1的情况下比ε=0.01具有更多的试探机会,因此会更早的发现最优动作。但在长远看来,ε=0.01最终的性能会比ε=0.1的方法更好(可以增加训练步数进行观察)。当然,为了充分利用高和低的ε优势,随着时刻的推移来减小ε往往会达到更好的效果。
3.2 非平稳问题
3.2.1算法介绍
在前面的讨论中,我们假设在一次学习过程中,每个臂杆的收益期望确定后,就不会随着训练步数的增加而变化,我们称之为平稳过程。而当赌博机的收益概率分布是随时间变化的,该问题就演化为了非平稳问题。不难理解,在非平稳问题的情况下,与本次动作间隔较远的动作收益往往有比较小的参考价值,因此此时再对前面动作的收益进行加和平均就剑走偏锋了。
此时可考虑采用一种近因加权的方法,即与本次动作相隔较近动作的实际收益赋的权值大些,比如采用如下的 ![]() 值的迭代公式:
值的迭代公式:
![]()
其中α为固定的迭代步长。通过对上式逐步的展开,可得到如下公式:
可见,随着动作序值的减小,其权值以指数级减小,这种加权方式称之为“指数近因加权”。
3.2.2 仿真程序
本仿真任务中老虎机的基本参数如下:
臂杆数:10;
学习次数:2000;
每次学习的训练步数:10000;
固定步长α:0.1
试探概率ε:0.1
初始每个臂杆的收益期望均为0,在每一步训练时都对10个臂杆的原收益期望加上一个均值为0,标准差为0.01的正态分布的增量。
每次动作的收益服从以选择臂杆的收益期望为均值,方差为1的正态分布。
此处将 ![]() 值的迭代公式进行如下更改:
值的迭代公式进行如下更改:
Q(action) = Q(action) + alpha * (reward - Q(action));%根据选择动作的估计收益3.2.3 仿真结果及说明
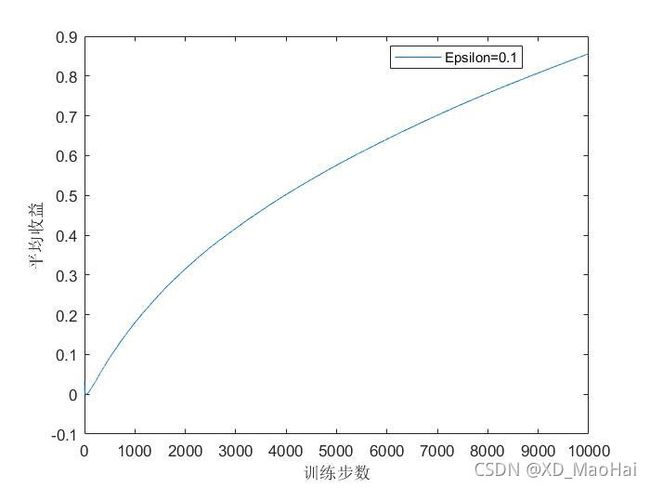
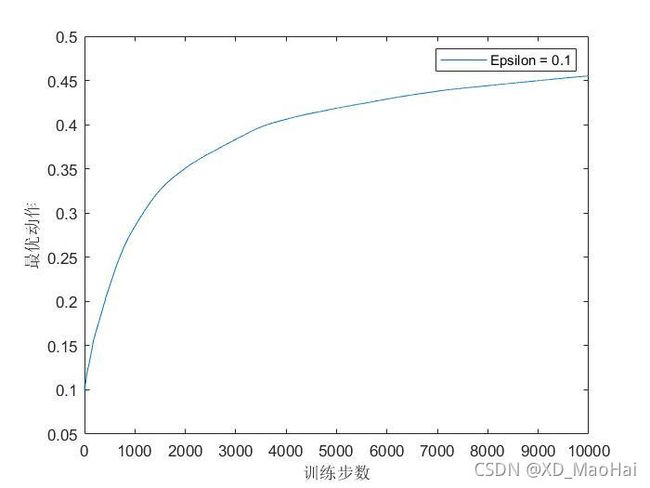
运行程序后,得到固定步长的ε-贪心算法结果如下:
为了对比,采用原 ![]() 值的迭代公式(采样平均方法,即将固定步长α换位1/n),得到结果如下:
值的迭代公式(采样平均方法,即将固定步长α换位1/n),得到结果如下:
对比可发现,对于非平稳问题,在两项评价指标中,采用固定步长的迭代方式要远胜于采样平均的方式。而一般的强化学习问题往往是非平稳的问题,但对于固定步长的迭代,收益往往无法收敛率不是很好,有时需要大量的调试才能得到一个满意的收敛率(对于符合收敛的步长序列可参《强化学习》P33)。
3.3 乐观初始值
3.3.1 算法介绍
在前面的讨论中,对于试探的力度,我们都是给予其一定的概率让其跳出贪婪的怪圈。除此之外,也可以给予![]() 以一定的初始值而非零,从而在训练前期加大试探力度。因为,对于服从均值为0,方差为1单位正态分布的实际收益期望,较高的初始值会使得在开始阶段,无论哪一种动作被选择,收益都比最开始的估计值要小,由此会降低对该动作的期望,转而偏向选择其它动作,即试探。
以一定的初始值而非零,从而在训练前期加大试探力度。因为,对于服从均值为0,方差为1单位正态分布的实际收益期望,较高的初始值会使得在开始阶段,无论哪一种动作被选择,收益都比最开始的估计值要小,由此会降低对该动作的期望,转而偏向选择其它动作,即试探。
3.3.2仿真程序
本仿真任务中赌博机的基本参数如下:
臂杆数:10;
学习次数:2000;
每次学习的训练步数:1000;
估计收益初始值
:5*ones(1,10)
10个臂杆的收益期望服从单位正态分布。
每次动作的收益服从以选择臂杆的收益期望为均值,方差为1的正态分布。
此处仅将第一段代码段中的初始值![]() 均换为5即可:
均换为5即可:
Q = 5*ones(1,ArmN)3.3.3 仿真结果及说明
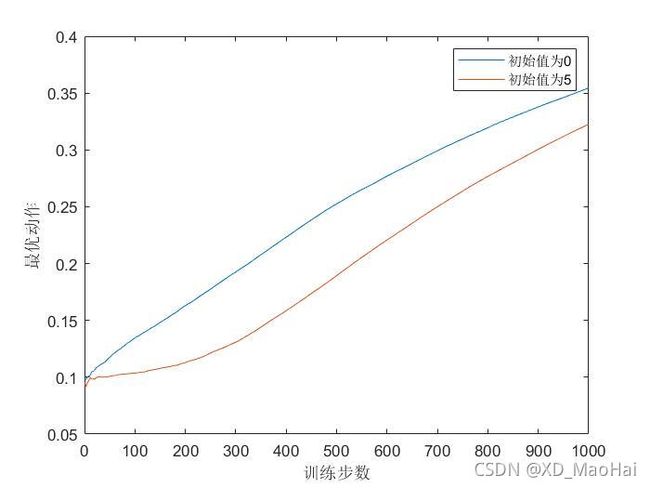
引入一般初始化(初始值为0)ε-贪心算法进行对比,两种方法都采用恒定步长,运行程序可得到结果图如下:
可见,刚开始时乐观初始值方法的表现比较差,因为它需要更多的试探,但随着时间的推移,试探的次数减少,表现得越来越好。但这种方法仅在平稳问题中表现较好,但在非平稳问题中,随着时间的推移,这种试探的力度会下降,但收益期望确依旧在变化。换句话说,这种试探的能力只是天生的。
3.4 无偏恒定步长技巧
3.4.1 算法介绍
目前为止我们讨论的所有方法都在一定程度上依赖于初值动作值![]() ,对于采样平均法来讲,当所有动作被选择一次时,初值动作值即会被实际收益取代,因此是无偏的;而对于步长为固定参数的情况,虽然这种偏差会随着训练次数的增多而减小,但不会消失,因此是有偏的,仿真图可见如下:
,对于采样平均法来讲,当所有动作被选择一次时,初值动作值即会被实际收益取代,因此是无偏的;而对于步长为固定参数的情况,虽然这种偏差会随着训练次数的增多而减小,但不会消失,因此是有偏的,仿真图可见如下:
而为了若得到一种对初始值无偏的指数近因加权方法,在《强化学习》这本书的P35页提出了一种无偏恒定步长技巧,即用修正因子来对恒定步长进行改善:
![]()
其中,α为恒定步长,![]() 为修正因子:
为修正因子:
![]()
利用待定参数法不难推出其通项为:
![]()
则有:
因此有:
![]()
可见当每个动作被选择一次时,其初始值即可被实际收益值替代,可证明其无偏性。
在该情况下将![]() 的迭代公式展开,可发现若要证明该方法的指数近因加权平均,只需证明前两项
的迭代公式展开,可发现若要证明该方法的指数近因加权平均,只需证明前两项![]() 的系数满足:
的系数满足:
因为有:
由此其指数近因加权平均性得证。
3.4.2 仿真程序
本仿真任务中老虎机的基本参数如下:
臂杆数:10;
学习次数:2000;
每次学习的训练步数:1000;
固定步长α:0.1
试探概率ε:0.1
初始每个臂杆的收益期望均为0,在每一步训练时都对10个臂杆的原收益期望加上一个均值为0,标准差为0.01的正态分布的增量。
每次动作的收益服从以选择臂杆的收益期望为均值,方差为1的正态分布。
此任务中将迭代步长改为如下:
Q(action) = Q(action) + alpha/(1-(1-alpha)^N(action)) * (reward - Q(action));3.4.3 仿真结果及说明
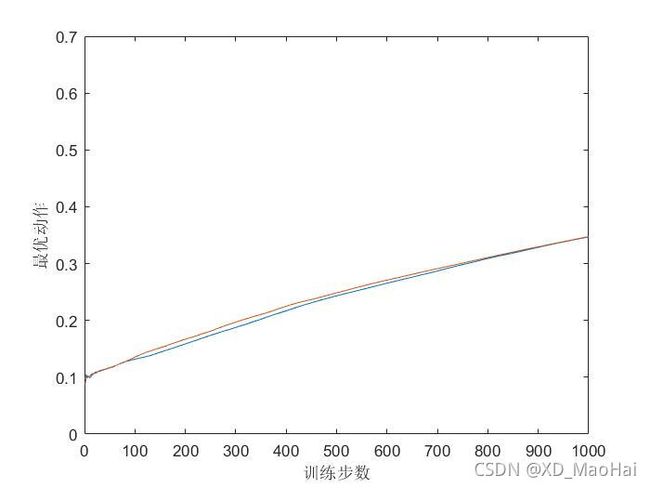
引入有初始值与无初始值做以对比,得到结果图如下:
可见该算法对初始值无偏。
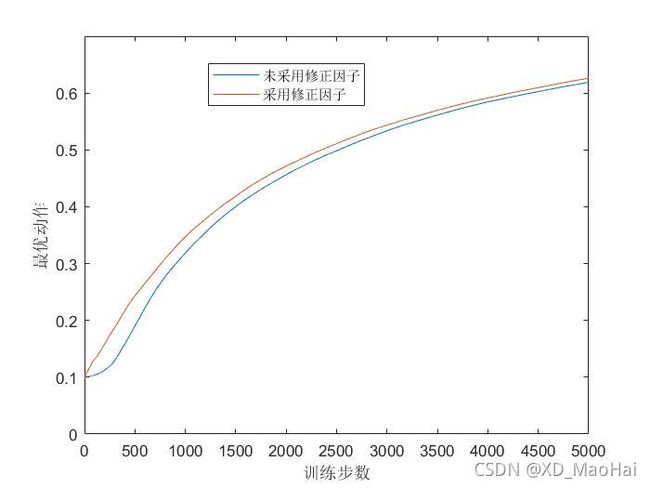
再对引入步长修正因子前后的结果图做一对比,并将训练周期增长至5000:
上面两图分别为有无初始值下,采用修正因子前后的结果图,对比可发现在有初值情况下采用修正因子的表现比较好,且对初始值无偏。
3.5 基于置信度上界(upper confidence bound)的动作选择(UCB算法)
3.5.1 算法介绍
虽然ε-贪心算法的会以一定概率进行试探,但这是一种盲目的选择(随机等概率选择),因为它不大会去选择接近贪心或者不确定性特别大的动作。而在非贪心动作中,最好是根据它们的潜力来选择可能事实上最优的动作,这就要考虑到它们的估计有多接近最大值,以及这些估计的不确定性。由此《强化学习》一书提出一种有效的方式来选择动作:
其中,![]() 表示t时刻之前动作a被选择的次数,c(c>0)可定性当做控制探测程度的因数。不难看出,根号内的项定性的反映了动作值估计的不确定性或方差的度量。因此,该值的大小是动作a的可能真实值上限,而c则决定了其置信水平。此外,随着训练步数的增加,被选择次数少的动作往往具有更多的试探价值,这也增加了试探力度。
表示t时刻之前动作a被选择的次数,c(c>0)可定性当做控制探测程度的因数。不难看出,根号内的项定性的反映了动作值估计的不确定性或方差的度量。因此,该值的大小是动作a的可能真实值上限,而c则决定了其置信水平。此外,随着训练步数的增加,被选择次数少的动作往往具有更多的试探价值,这也增加了试探力度。
3.5.2 仿真程序
本仿真任务中老虎机的基本参数如下:
臂杆数:10;
学习次数:2000;
每次学习的训练步数:1000;
10个臂杆的收益期望服从单位正态分布;
每次动作的收益服从以选择臂杆的收益期望为均值,方差为1的正态分布。
此任务中将动作选择公式改为如下:
[Qmax,i] = max(Q+c*sqrt(log(n)./N)); %根据估计收益选出最优收益和最优动作3.5.3 仿真结果及说明
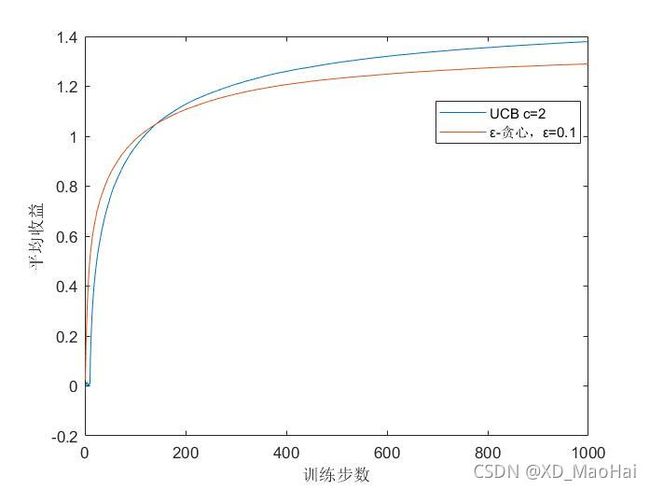
引入ε-贪心算法做以对比,得到结果图如下:
可见,在开始时UCB的表现并不如ε-贪心算法的表现好,这是因为UCB在训练前期付诸了更多的试探。而从长远看来,UCB的表现要比ε-贪心算法的好,这是因为UCB在积累了一定的经验后,根号项的值已经逐渐被动作估计值![]() 淹没,增加了开发力度,而不是还在傻乎乎的盲目试探,这也是其优势所在。
淹没,增加了开发力度,而不是还在傻乎乎的盲目试探,这也是其优势所在。
3.6 梯度赌博机算法
3.6.1 算法介绍
前述方法都主要依据对动作的估计值![]() 进行动作选择,但这不是唯一的动作选择方法,初次之外,我们可以引入一个偏好函数
进行动作选择,但这不是唯一的动作选择方法,初次之外,我们可以引入一个偏好函数![]() ,而每个动作的选择概率则是关于
,而每个动作的选择概率则是关于![]() 的softmax分布:
的softmax分布:
在选择动作![]() 并得到得到收益
并得到得到收益![]() 后,根据以下式子对动作
后,根据以下式子对动作![]() 进行偏好函数的更新:
进行偏好函数的更新:
![]()
而对于其它动作则根据如下式子更新:
![]()
其中α为迭代步长,基准项![]() 为时刻t内所有收益的平均值。根据上面更新迭代的两式的确无法直观的看出以往收益对动作选择的影响,但若将以上两式写为如下式子即可看出迭代原理:
为时刻t内所有收益的平均值。根据上面更新迭代的两式的确无法直观的看出以往收益对动作选择的影响,但若将以上两式写为如下式子即可看出迭代原理:
这就是期望收益的梯度公式。其中![]() 为总体的期望收益:
为总体的期望收益:
根据《强化学习》P38-40的证明(此处由于篇幅不再赘述),可得到梯度赌博机算法的期望更新与期望收益的梯度是相等的。而根据期望收益的梯度公式,可以看到,每一个动作的偏好函数![]() 与增量对总体期望收益的影响成正比,并且
与增量对总体期望收益的影响成正比,并且![]() 越大,其对应的动作选择概率就越大,这也是梯度算法的本质。
越大,其对应的动作选择概率就越大,这也是梯度算法的本质。
3.6.2 仿真程序
本仿真任务中老虎机的基本参数如下:
臂杆数:10;
学习次数:2000;
每次学习的训练步数:1000;
偏好函数初值:zeros(1,10)
步长参数α:0.1,0.4
10个臂杆的收益期望服从单位正态分布;
每次动作的收益服从以选择臂杆的收益期望为均值,方差为1的正态分布。
此处给出给算法的完整仿真代码如下:
%% 参数初始化
clc,clear;
ArmN = 10; %老虎机臂(可选动作)数
alpha = 0.4; %步长
TrialN = 1000; %每次学习的实验次数(训练步数)
LearnN = 2000; %总学习次数
Range = 1:TrialN; %1-1000递增序列
%% 训练过程
OpAction_set = zeros(1,TrialN); %存放单次训练最优动作比率的数组
OpAction_total_set = zeros(1,TrialN);%存放全局最优动作比率的数组
for m = 1:LearnN
H = zeros(1,ArmN); %偏好函数
reward_total = 0; %平均收益
Value = randn([1 ArmN]); %根据单位正态分布产生各动作的收益期望
OpAction = 0; %最优动作比率初始化
[Value_max,Value_max_a] = max(Value);%选出最优动作
Q = zeros(1,ArmN); %各动作估计收益初始化
N = zeros(1,ArmN); %各动作选择次数初始化
for n = 1:TrialN %开始单次学习训练
[Action_i,Pro] = SelectAct(H); %根据估计收益选出最优收益和最优动作
reward = normrnd(Value(Action_i),1); %以均值为Value(action)、方差为1的正态分布产生实际收益
reward_total = reward_total + 1/n * (reward-reward_total); %更新平均收益
if (Action_i==Value_max_a) %判断是否为最优动作
OpAction = OpAction + 1;
end
OpAction_set(n) = OpAction; %填充最优动作次数数组
H = H - alpha*(reward-reward_total)*Pro;
H(Action_i) = H(Action_i) + alpha * (reward-reward_total);
end
OpAction_total_set = OpAction_total_set + 1/m * (OpAction_set - OpAction_total_set);%更新最优动作次数数组
end
%绘制最优动作比率随训练步数变化的图线
OpAction_total_set = OpAction_total_set ./ Range;%将次数化为比率
plot(OpAction_total_set);
xlabel('训练步数');ylabel('最优动作');
其中函数SelectAct函数完成的是通过输入偏好函数H,输出选择的动作Action_i以及各动作选择概率Pro,其代码如下
function [Action_i,Pro] = SelectAct(H)
Pro = exp(H) ./ sum(exp(H));
Pro_reg = zeros(length(H));
Pro_reg(1) = Pro(1);
for i = 2:length(H)
Pro_reg(i) = Pro(i) + Pro_reg(i-1);
end
Pro_reg = Pro_reg - rand(1);
Action_i = find(Pro_reg>=0,1);
end3.6.3 仿真结果及说明
通过运行程序得到结果如下:
可见 一定范围内,在迭代步长越大时试探的力度会比较小,较快的收敛,并且最终收益表现较差,而较小的迭代步长则恰恰相反。
四、总结
在探究了这么多算法后,为了比较这些算法的优劣,《强化学习》一书将这些算法的学习曲线绘制在了一张图上进行比较:
可见,总的来说UCB算法似乎表现得更好。
此外,回望我的成长历程,每个人生节点同样也是一次次选择,然而,由于大人所谓的经验以及来自同龄人的压力,我们的选择空间都出奇的逼仄,有时连仅存的兴趣与天马行空的勇气也都淹没在了对短期目标的疯狂追求中。在这样的贪婪循环中,诚然我们可能会达到那些过来人经验论中的最高点,然而通往真正适合自己的、能带给我们更多欢悦与审视空间的圣城的道路,我们甚至没有去涉足的机会与勇气,并最后也成为那个后来人中的“过来人”。
王小波先生的笔下有只特立独行的猪,无视命运既定的设置,不惧人们的恐吓,常常跳出猪圈“拈花惹草”,学汽笛声与知青们嬉戏,它的一生遇见了太多种猪不敢瞻望的风景。王小波先生在文末写到,“我已经四十岁了,除了这只猪,还没见过谁敢于如此无视生活的设置”。
也许有时,我们仅仅缺少那股翻越猪圈的勇气。



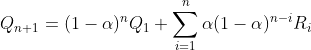



![A_{t}\doteq \underset{a}{argmax}[Q_{t}(a)+c\sqrt{{ \frac{lnt}{N_{t}(a)}}}]](http://img.e-com-net.com/image/info8/f3612e18455245af90d05b6835ca834d.gif)