OpenCV（十六）边缘检测2 -- Laplace(拉普拉斯)二阶微分算子

目录

一、基础理论

1、原理 

2、过程

3、Laplacian函数

代码

效果

参考资料

---

一、基础理论

1、原理 

Laplace算子作为边缘检测之一，和Sobel算子一样也是工程数学中常用的一种积分变换，属于空间锐化滤波操作。因为图像是二维的，所以需要在两个方向求导。

定义：

拉普拉斯算子（Laplace Operator）是n维欧几里德空间中的一个二阶微分算子，定义为梯度（▽f）的散度（▽·f）。拉普拉斯算子也可以推广为定义在黎曼流形上的椭圆型算子，称为拉普拉斯-贝尔特拉米算子。

原理：

拉普拉斯算子是二阶微分线性算子，在图像边缘处理中，二阶微分的边缘定位能力更强，锐化效果更好，因此在进行图像边缘处理时，直接采用二阶微分算子而不使用一阶微分。

2、过程

1、一维一阶差分公式和二阶差分公式分别为：

2、在一个二维函数f(x,y)中，x,y两个方向的二阶差分分别为：

3、所以，Laplace算子的差分形式为： 

 

4、得到卷积核：

 5、扩展卷积核

该卷积核在上下左右四个90度的方向上结果相同，也就是说在90度方向上无方向性。为了让该卷积核在45度的方向上也能具有该性质，对它扩展定义：

3、Laplacian函数

C++： 

void Laplacian(InputArray src, OutputArray dst, int ddepth, int ksize=1, double scale=1, double delta=0, int borderType=BORDER_DEFAULT )

Laplacian(src, dst, CV_16S, 3);                             //拉普拉斯变换
    //         深度        核大小

python：

# 2、Laplacian 算子
laplacian = cv.Laplacian(dst, cv.CV_64F)

代码

C++：

//拉普拉斯变换
#include
#include
using namespace cv;

Mat src, dst, abs_dst_laplace;

int main()
{
    
    src = imread("Resource/test13.jpg");
    imshow("原图", src);

    //拉普拉斯变换
    Laplacian(src, dst, CV_16S, 3);                     //拉普拉斯变换
    //                          深度      核大小
    convertScaleAbs(dst, abs_dst_laplace);              //将类型转化为CV_8UC1
    imshow("laplacian", abs_dst_laplace);    
   
    waitKey(0);
}

python：

# 边缘检测（Sobel、Laplace、Canny）
import cv2 as cv

# Laplace二阶微分算子
def Laplace():
    # 1、高斯滤波器 (3 X 3)
    dst = cv.GaussianBlur(img, (3, 3), sigmaX=0.1)
    #                           核大小  在X方向上的标准偏差

    # 2、Laplacian 算子
    laplacian = cv.Laplacian(dst, cv.CV_64F)

    # 3、取绝对值
    laplacian = cv.convertScaleAbs(laplacian)

    # 4、显示
    cv.imshow("laplacian", laplacian)


if __name__ == '__main__':
    # 读取图片
    img = cv.imread("Resource/test5.jpg")
    cv.imshow("img", img)

    # Sobel()         #Sobel一阶微分算子
    Laplace()       #Laplace二阶微分算子

    cv.waitKey(0)

 

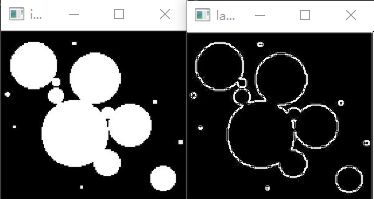
效果

 

参考资料

https://blog.csdn.net/hellocsz/article/details/102485387?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522162899470416780357226662%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=162899470416780357226662&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_click~default-2-102485387.ecpm_v1_rank_v29&utm_term=%E6%8B%89%E6%99%AE%E6%8B%89%E6%96%AF%E7%AE%97%E5%AD%90&spm=1018.2226.3001.4187

https://www.bilibili.com/video/BV1Fo4y1d7JL?p=34&spm_id_from=pageDriver