CenterNet算法详解
Objects as Points-论文链接-代码链接
目录
-
- 1、需求解读
- 2、CenterNet算法简介
- 3、CenterNet算法详解
-
- 3.1 CenterNet网络结构
- 3.2 CenterNet实现细节详解
-
- 3.2.1 训练阶段Heatmap生成
- 3.2.2 Heatmap上应用高斯核
- 3.3 CenterNet损失函数
-
- 3.3.1 Heatmap损失函数
- 3.3.2 中心点偏移损失函数
- 3.3.3 目标长宽损失函数
- 3.4 CenterNet推理阶段
- 4、CenterNet网络代码实现
- 5、CenterNet效果展示与分析
-
- 5.1 CenterNet客观效果展示与分析
- 5.2 CenterNet主观效果展示与分析
- 6、总结与分析
- 参考资料
- 注意事项
1、需求解读
随着基于Anchor的目标检测性能达到了极限,基于Anchor-free的目标检测算法成为了当前的研究热点,具有代表性的工作包括CornerNet、FOCS与CenterNet等。除此之外,基于Anchor的目标检测算法存在着一些严重的问题,具体包括:(1)Anchros的定义在一定程度上会限制检测算法的性能;(2)NMS等后处理操作会降低整个检测算法的速度。为了解决这些问题,基于Anchor-free的目标检测算法应运而生,本文对CenterNet目标检测算法进行详细的剖析。
2、CenterNet算法简介
CenterNet是一个基于Anchor-free的目标检测算法,该算法是在CornerNet算法的基础上改进而来的。与单阶段目标检测算法yolov3相比,该算法在保证速度的前提下,精度提升了4个百分点。与其它的单阶段或者双阶段目标检测算法相比,该算法具有以下的优势:
- (1)该算法去除低效复杂的Anchors操作,进一步提升了检测算法性能;
- (2)该算法直接在heatmap图上面执行了过滤操作,去除了耗时的NMS后处理操作,进一步提升了整个算法的运行速度;
- (3)该算法不仅可以应用到2D目标检测中,经过简单的改变它还可以应用3D目标检测与人体关键点检测等其它的任务中,即具有很好的通用性。
3、CenterNet算法详解
3.1 CenterNet网络结构

上图展示了CenterNet网络的整体结构,整个网络结构比较简单。
- (1)最左边表示输入图片。输入图片需要裁减到512*512大小,即长边缩放到512,短边补0,具体的效果如下图所示,由于原图的W>512,因而直接将其缩放为512;由于原图的H<512,因而对其执行补0操作;
- (2)中间表示基准网络,论文中尝试了Hourglass、ResNet与DLA3种网络架构,各个网络架构的精度及帧率为:Resnet-18 with up-convolutional layers:28.1% coco and 142 FPS、DLA-34:37.4% COCOAP and 52 FPS、Hourglass-104:45.1% COCOAP and 1.4 FPS。

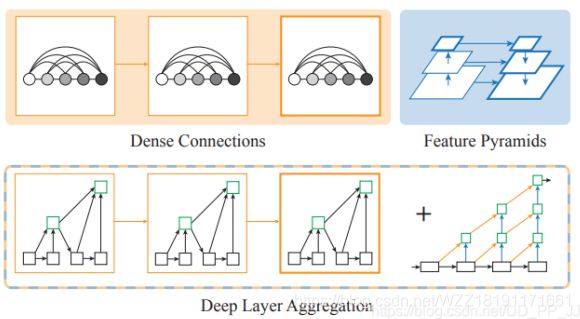
上图展示了3中不同的网络架构,图(a)表示Hourglass网络,该网络是在ECCV2016中的Stacked hourglass networks for human pose estimation论文中提出的一种网络,用来解决人体位姿估计问题,其思路主要通过将多个漏斗形状的网络堆叠起来,从而获得多尺度信息,具体的细节请参考该博客。图(b)表示带有反卷积的ResNet网络,作者在每一个上采样层之前增加了一个3*3的膨胀卷积,即先使用反卷积来改变膨胀卷积的通道个数,然后使用反卷积来对特征映射执行上采样操作。图©表示用于语义分割的DLA34网络;图d表示改变的DLA34网络,该网络在原始的DLA34网络的基础上增加了更多的残差连接,该网络将Dense_Connection与FPN的思路融合起来,前者源于DenseNet,可以用来聚合语义信息,能够提升模型推断是“what”的能力;后者源于聚合空间信息,能够提升模型推断在“where”的能力,具体的细节如下图所示。
- (3)最右边表示预测模块,该模块包含3个分支,具体包括中心点heatmap图分支、中心点offset分支、目标大小分支。heatmap图分支包含C个通道,每一个通道包含一个类别,heatmap中白色的亮区域表示目标的中心 点位置;中心点offset分支用来弥补将池化后的低heatmap上的点映射到原图中所带来的像素误差;目标大小分支用来预测目标矩形框的w与h偏差值。
3.2 CenterNet实现细节详解
3.2.1 训练阶段Heatmap生成
CenterNet将目标检测问题转换成中心点预测问题,即用目标的中心点来表示该目标,并通过预测目标中心点的偏移量与宽高来获取目标的矩形框。Heatmap表示分类信息,每一个类别将会产生一个单独的Heatmap图。对于每张Heatmap图而言,当某个坐标处包含目标的中心点时,则会在该目标处产生一个关键点,我们利用高斯圆来表示整个关键点,下图展示了具体的细节。

生成Heatmap图的具体步骤如下所示:
-
步骤1-将输入的图片缩放成512*512大小,对该图像执行R=4的下采样操作之后,获得一个128*128大小的Heatmap图;
-
步骤2-将输入图片中的Box缩放到128*128大小的Heatmap图上面,计算该Box的中心点坐标,并执行向下取整操作,并将其定义为point;
-
步骤3-根据目标Box大小来计算高斯圆的半径R;
关于高斯圆的半径确定,主要还是依赖于目标box的宽高, 实际情况下通常会取IOU=0.7,即下图中的overlap=0.7作为临界值,然后分别计算出三种情况的半径,取最小值作为高斯核的半径R,具体的实现细节如下图所示:
(1)情况1-预测框pred_bbox包含gt_bbox框,对应于下图中的第1种情况,将整个IoU公式展开之后,成为一个二元一次方程的求解问题。
(2)情况2-gt_bbox包含预测框pred_bbox框,对应于下图中的第2种情况,将整个IoU公式展开之后,成为一个二元一次方程的求解问题。
(3)情况3-gt_bbox与预测框pred_bbox框相互重叠,对应于下图中的第3种情况,将整个IoU公式展开之后,成为一个二元一次方程的求解问题。

-
步骤4-在128*128大小的Heatmap图上面,以point为中心点,半径为R计算高斯值,point点处数值最大,随着半径R的增加数值不断减小;

上图展示了一个样例,左边表示经过裁剪之后的512512大小的输入图片,右边表示经过高斯操作之后生成的128128大小的Heatmap图。由于图中包含两只猫,这两只猫属于一个类别,因此在同一个Heatmap图上面生成了两个高斯圆,高斯圆的大小与矩形框的大小有关。
3.2.2 Heatmap上应用高斯核
Heatmap上的关键点之所以采用二维高斯核来表示,是由于对于在目标中心点附近的一些点,其预测出来的pre_box和gt_box的IOU可能会大于0.7,不能直接对这些预测值进行惩罚,需要温和一点,所以采用高斯核。该问题在Corner算法中就已经存在,如下图所示,我们在设置gt_bbox的heatmap时,不仅仅只在中心点的位置设置标签1,图中红色的矩形框表示gt_bbox,但是绿色的矩形框其实也可以很好的包围该目标,即我们在检测的过程中如何获得像绿色框这样的矩形框时,我们也要保存它。通俗一点来讲,只要预测的corner点在中心点的某一个半径r内,而且该矩形框与gt_bbox之间的IoU大于0.7时,我们将这些点处的值设置为一个高斯分布的数值,而不是数值0。

3.3 CenterNet损失函数
整个CenterNet的损失函数包含3个部分, L k L_{k} Lk表示 heatmap中心点损失, L o f f L_{off} Loff表示目标中心点偏移损失, L s i z e L_{size} Lsize表示目标长宽损失函数。

3.3.1 Heatmap损失函数

上图展示了Heatmap损失函数,该函数是在Focal Loss的基础上进行了改进,其中的 α \alpha α与 β \beta β是两个超参数,用来均衡难易样本; Y x y c Y_{xyc} Yxyc表示GT值, Y ^ x y c \hat{Y} _{xyc} Y^xyc表示预测值;N表示关键点的个数。
- 当 Y ^ x y c \hat{Y} _{xyc} Y^xyc=1时,易分类样本的预测值接近为1,此时 ( 1 − Y ^ x y c ) α ({1-\hat{Y} _{xyc}})^{\alpha } (1−Y^xyc)α就表示一个很小的数值,此时损失函数的数值就比较小,起到了降低该样本权重的作用。
- 当 Y ^ x y c \hat{Y} _{xyc} Y^xyc=1时,难分类样本的预测值接近为0,此时 ( 1 − Y ^ x y c ) α ({1-\hat{Y} _{xyc}})^{\alpha } (1−Y^xyc)α就表示一个较大的数值,此时损失函数的数值就比较大,起到了增加该样本权重的作用。
- 当 Y ^ x y c \hat{Y} _{xyc} Y^xyc!=1时,为了防止预测值 Y ^ x y c \hat{Y} _{xyc} Y^xyc过高的接近于1,利用 ( 1 − Y ^ x y c ) α ({1-\hat{Y} _{xyc}})^{\alpha } (1−Y^xyc)α来充当惩罚项,而 ( 1 − Y x y c ) β ({1-{Y} _{xyc}})^{\beta } (1−Yxyc)β这个参数距离中心点越近,其数值越小,用来进一步减轻这个惩罚力度。
3.3.2 中心点偏移损失函数
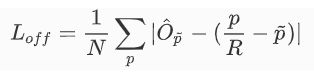
上图展示了 L o f f L_{off} Loff损失函数,其中 O ^ p ~ { \hat{O} \tilde{p} } O^p~表示网络预测的偏移量数值,p表示图像中心点坐标,R表示Heatmap的缩放因子, p ~ \tilde{p} p~表示缩放后中心点的近似整数坐标,整个过程利用L1 Loss计算正样本块的偏移损失。由于骨干网络输出的 feature map 的空间分辨率是原始输入图像的四分之一。即输出 feature map 上的每一个像素点对应到原始图像的一个4x4 区域,这会带来较大的误差,因此引入了偏置的损失值。
假设目标中心点p为(125, 63),由于输入图片大小为512*512,缩放尺度R=4,因此缩放后的128x128尺寸下中心点坐标为(31.25, 15.75), 相对于整数坐标(31, 15)的偏移值即为(0.25, 0.75)。
3.3.3 目标长宽损失函数
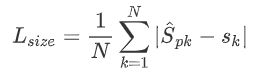
上图展示了目标长宽损失函数,其中N表示关键点的个数,Sk表示目标的真实尺寸, S ^ p k {\hat{S} pk} S^pk表示预测的尺寸,整个过程利用L1 Loss来计算正样本块的长宽损失。
3.4 CenterNet推理阶段
CenterNet网络的推理阶段的实现步骤如下所述:
- 步骤1-首先将输入图片缩到512*512大小;
- 步骤2-然后对输入图片执行下采样,并对下采样后的图像执行预测,即在128*128大小的Heatmap上执行预测;
- 步骤3-然后在128*128大小的Heatmap图上面采用一个3*3大小的最大池化操作来获取Heatmap中满足条件的关键点(类似于anchor-based检测中nms的效果),并选取100个关键点;
- 步骤4-最后根据confidence阈值来过滤出最终的检测结果。
4、CenterNet网络代码实现
1、Hourglass网络部分代码
class convolution(nn.Module):
def __init__(self, k, inp_dim, out_dim, stride=1, with_bn=True):
super(convolution, self).__init__()
pad = (k - 1) // 2
self.conv = nn.Conv2d(inp_dim, out_dim, (k, k), padding=(pad, pad), stride=(stride, stride), bias=not with_bn)
self.bn = nn.BatchNorm2d(out_dim) if with_bn else nn.Sequential()
self.relu = nn.ReLU(inplace=True)
def forward(self, x):
conv = self.conv(x)
bn = self.bn(conv)
relu = self.relu(bn)
return relu
class fully_connected(nn.Module):
def __init__(self, inp_dim, out_dim, with_bn=True):
super(fully_connected, self).__init__()
self.with_bn = with_bn
self.linear = nn.Linear(inp_dim, out_dim)
if self.with_bn:
self.bn = nn.BatchNorm1d(out_dim)
self.relu = nn.ReLU(inplace=True)
def forward(self, x):
linear = self.linear(x)
bn = self.bn(linear) if self.with_bn else linear
relu = self.relu(bn)
return relu
class residual(nn.Module):
def __init__(self, k, inp_dim, out_dim, stride=1, with_bn=True):
super(residual, self).__init__()
self.conv1 = nn.Conv2d(inp_dim, out_dim, (3, 3), padding=(1, 1), stride=(stride, stride), bias=False)
self.bn1 = nn.BatchNorm2d(out_dim)
self.relu1 = nn.ReLU(inplace=True)
self.conv2 = nn.Conv2d(out_dim, out_dim, (3, 3), padding=(1, 1), bias=False)
self.bn2 = nn.BatchNorm2d(out_dim)
self.skip = nn.Sequential(
nn.Conv2d(inp_dim, out_dim, (1, 1), stride=(stride, stride), bias=False),
nn.BatchNorm2d(out_dim)
) if stride != 1 or inp_dim != out_dim else nn.Sequential()
self.relu = nn.ReLU(inplace=True)
def forward(self, x):
conv1 = self.conv1(x)
bn1 = self.bn1(conv1)
relu1 = self.relu1(bn1)
conv2 = self.conv2(relu1)
bn2 = self.bn2(conv2)
skip = self.skip(x)
return self.relu(bn2 + skip)
def make_layer(k, inp_dim, out_dim, modules, layer=convolution, **kwargs):
layers = [layer(k, inp_dim, out_dim, **kwargs)]
for _ in range(1, modules):
layers.append(layer(k, out_dim, out_dim, **kwargs))
return nn.Sequential(*layers)
def make_layer_revr(k, inp_dim, out_dim, modules, layer=convolution, **kwargs):
layers = []
for _ in range(modules - 1):
layers.append(layer(k, inp_dim, inp_dim, **kwargs))
layers.append(layer(k, inp_dim, out_dim, **kwargs))
return nn.Sequential(*layers)
class MergeUp(nn.Module):
def forward(self, up1, up2):
return up1 + up2
def make_merge_layer(dim):
return MergeUp()
# def make_pool_layer(dim):
# return nn.MaxPool2d(kernel_size=2, stride=2)
def make_pool_layer(dim):
return nn.Sequential()
def make_unpool_layer(dim):
return nn.Upsample(scale_factor=2)
def make_kp_layer(cnv_dim, curr_dim, out_dim):
return nn.Sequential(
convolution(3, cnv_dim, curr_dim, with_bn=False),
nn.Conv2d(curr_dim, out_dim, (1, 1))
)
def make_inter_layer(dim):
return residual(3, dim, dim)
def make_cnv_layer(inp_dim, out_dim):
return convolution(3, inp_dim, out_dim)
class kp_module(nn.Module):
def __init__(
self, n, dims, modules, layer=residual,
make_up_layer=make_layer, make_low_layer=make_layer,
make_hg_layer=make_layer, make_hg_layer_revr=make_layer_revr,
make_pool_layer=make_pool_layer, make_unpool_layer=make_unpool_layer,
make_merge_layer=make_merge_layer, **kwargs
):
super(kp_module, self).__init__()
self.n = n
curr_mod = modules[0]
next_mod = modules[1]
curr_dim = dims[0]
next_dim = dims[1]
self.up1 = make_up_layer(
3, curr_dim, curr_dim, curr_mod,
layer=layer, **kwargs
)
self.max1 = make_pool_layer(curr_dim)
self.low1 = make_hg_layer(
3, curr_dim, next_dim, curr_mod,
layer=layer, **kwargs
)
self.low2 = kp_module(
n - 1, dims[1:], modules[1:], layer=layer,
make_up_layer=make_up_layer,
make_low_layer=make_low_layer,
make_hg_layer=make_hg_layer,
make_hg_layer_revr=make_hg_layer_revr,
make_pool_layer=make_pool_layer,
make_unpool_layer=make_unpool_layer,
make_merge_layer=make_merge_layer,
**kwargs
) if self.n > 1 else \
make_low_layer(
3, next_dim, next_dim, next_mod,
layer=layer, **kwargs
)
self.low3 = make_hg_layer_revr(
3, next_dim, curr_dim, curr_mod,
layer=layer, **kwargs
)
self.up2 = make_unpool_layer(curr_dim)
self.merge = make_merge_layer(curr_dim)
def forward(self, x):
up1 = self.up1(x)
max1 = self.max1(x)
low1 = self.low1(max1)
low2 = self.low2(low1)
low3 = self.low3(low2)
up2 = self.up2(low3)
return self.merge(up1, up2)
class exkp(nn.Module):
def __init__(
self, n, nstack, dims, modules, heads, pre=None, cnv_dim=256,
make_tl_layer=None, make_br_layer=None,
make_cnv_layer=make_cnv_layer, make_heat_layer=make_kp_layer,
make_tag_layer=make_kp_layer, make_regr_layer=make_kp_layer,
make_up_layer=make_layer, make_low_layer=make_layer,
make_hg_layer=make_layer, make_hg_layer_revr=make_layer_revr,
make_pool_layer=make_pool_layer, make_unpool_layer=make_unpool_layer,
make_merge_layer=make_merge_layer, make_inter_layer=make_inter_layer,
kp_layer=residual
):
super(exkp, self).__init__()
self.nstack = nstack
self.heads = heads
curr_dim = dims[0]
self.pre = nn.Sequential(
convolution(7, 3, 128, stride=2),
residual(3, 128, 256, stride=2)
) if pre is None else pre
self.kps = nn.ModuleList([
kp_module(
n, dims, modules, layer=kp_layer,
make_up_layer=make_up_layer,
make_low_layer=make_low_layer,
make_hg_layer=make_hg_layer,
make_hg_layer_revr=make_hg_layer_revr,
make_pool_layer=make_pool_layer,
make_unpool_layer=make_unpool_layer,
make_merge_layer=make_merge_layer
) for _ in range(nstack)
])
self.cnvs = nn.ModuleList([
make_cnv_layer(curr_dim, cnv_dim) for _ in range(nstack)
])
self.inters = nn.ModuleList([
make_inter_layer(curr_dim) for _ in range(nstack - 1)
])
self.inters_ = nn.ModuleList([
nn.Sequential(
nn.Conv2d(curr_dim, curr_dim, (1, 1), bias=False),
nn.BatchNorm2d(curr_dim)
) for _ in range(nstack - 1)
])
self.cnvs_ = nn.ModuleList([
nn.Sequential(
nn.Conv2d(cnv_dim, curr_dim, (1, 1), bias=False),
nn.BatchNorm2d(curr_dim)
) for _ in range(nstack - 1)
])
## keypoint heatmaps
for head in heads.keys():
if 'hm' in head:
module = nn.ModuleList([
make_heat_layer(
cnv_dim, curr_dim, heads[head]) for _ in range(nstack)
])
self.__setattr__(head, module)
for heat in self.__getattr__(head):
heat[-1].bias.data.fill_(-2.19)
else:
module = nn.ModuleList([
make_regr_layer(
cnv_dim, curr_dim, heads[head]) for _ in range(nstack)
])
self.__setattr__(head, module)
self.relu = nn.ReLU(inplace=True)
def forward(self, image):
# print('image shape', image.shape)
inter = self.pre(image)
outs = []
for ind in range(self.nstack):
kp_, cnv_ = self.kps[ind], self.cnvs[ind]
kp = kp_(inter)
cnv = cnv_(kp)
out = {}
for head in self.heads:
layer = self.__getattr__(head)[ind]
y = layer(cnv)
out[head] = y
outs.append(out)
if ind < self.nstack - 1:
inter = self.inters_[ind](inter) + self.cnvs_[ind](cnv)
inter = self.relu(inter)
inter = self.inters[ind](inter)
return outs
def make_hg_layer(kernel, dim0, dim1, mod, layer=convolution, **kwargs):
layers = [layer(kernel, dim0, dim1, stride=2)]
layers += [layer(kernel, dim1, dim1) for _ in range(mod - 1)]
return nn.Sequential(*layers)
class HourglassNet(exkp):
def __init__(self, heads, num_stacks=2):
n = 5
dims = [256, 256, 384, 384, 384, 512]
modules = [2, 2, 2, 2, 2, 4]
super(HourglassNet, self).__init__(
n, num_stacks, dims, modules, heads,
make_tl_layer=None,
make_br_layer=None,
make_pool_layer=make_pool_layer,
make_hg_layer=make_hg_layer,
kp_layer=residual, cnv_dim=256
)
def get_large_hourglass_net(num_layers, heads, head_conv):
model = HourglassNet(heads, 2)
return model
5、CenterNet效果展示与分析
5.1 CenterNet客观效果展示与分析
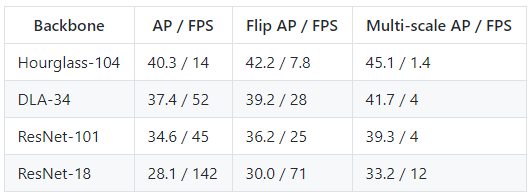
上表展示了CenterNet目标检测在COCO验证集上面的精度与速度。第1行展示了利用Hourglass-104作为基准网络后不仅能够获得40.4AP,而且可以获得14FPS的速度;第2行展示了利用DLA-34作为基准网络后获得的AP与FPS;第3行与第4行分别展示了ResNet-101与ResNet-18基准网络在COCO验证集上面的效果。通过观察我们可以发现,基于DLA-34的基准网络能够在精度与速度之间达到一个折中。

上表展示了CenterNet算法在COCO关键点验证集上面的测试效果。通过观察我们可以得出以下的初步结论:(1)基于Hourglass的基准网络可以获得更高的精度,但是速度却很难满足实时场景的需求;(2)基于DLA-34的基准网络不仅可以获得更高的精度,而且可以获得较好的精度。(3)该算法的精度接近于很多state-of-art的行人位姿估计算法。
5.2 CenterNet主观效果展示与分析

上图展示了CenterNet检测算法在一张测试图片上面的测试结果。左边展示的是对应的Heatmap图,图中的褐色点表示该算法输出的中心点坐标,右边表示该算法的检测结果。

上图展示了CenterNet人体位姿估计算法在一张测试图片上面的测试结果。最左边展示的是目标中心点的Heatmap图,中间图表示的是输出的人体关键点Heatmap图,最右边表示的是CenterNet人体位姿估计算法的输出结果,该算法在这种复杂的场景下仍然获得了较高的精度。

上图展示了CenterNet目标检测算法、CenterNet人体位姿估计算法、CenterNet 3D目标检测算法在一些复杂的测试场景上面的测试效果。通过观察我们可以发现该算法在不同的复杂场景下仍然得到较高的精度。
6、总结与分析

CenterNet是一个基于Anchor-free的目标检测算法。通过观察上图,我们可以发现该算法的精度几乎超过了当时所有的单阶段与双阶段目标检测算法,包括Faster-RCNN、RetinaNet和Yolov3。由于该算法去除了耗时的Anchors与NMS后处理操作,因而该算法具有较快的运行速度,适合部署在一些低性能的嵌入式设备中。除此之外,经过实际的测试我们会发现该算法在多个实际场景中都能取得较高的检测精度。
参考资料
[1] 原始论文
[2] 博客1
[3] 博客2
注意事项
[1] 该博客是本人原创博客,如果您对该博客感兴趣,想要转载该博客,请与我联系(qq邮箱:[email protected]),我会在第一时间回复大家,谢谢大家的关注。
[2] 由于个人能力有限,该博客可能存在很多的问题,希望大家能够提出改进意见。
[3] 如果您在阅读本博客时遇到不理解的地方,希望您可以联系我,我会及时的回复您,和您交流想法和意见,谢谢。
[4] 本人业余时间承接各种本科毕设设计和各种项目,包括图像处理(数据挖掘、机器学习、深度学习等)、matlab仿真、python算法及仿真等,有需要的请加QQ:1575262785详聊,备注“项目”!!!
