深度学习之NLP学习笔记（四）——Transformer模型

参考文章

关于transformer的解读1

关于transformer的解读2

Transformer所使用的注意力机制的核心思想是去计算一句话中的每个词对于这句话中所有词的相互关系，然后认为这些词与词之间的相互关系在一定程度上反应了这句话中不同词之间的关联性以及重要程度。因此再利用这些相互关系来调整每个词的重要性（权重）就可以获得每个词新的表达。这个新的表征不但蕴含了该词本身，还蕴含了其他词与这个词的关系，因此和单纯的词向量相比是一个更加全局的表达。

---

注意力相关知识

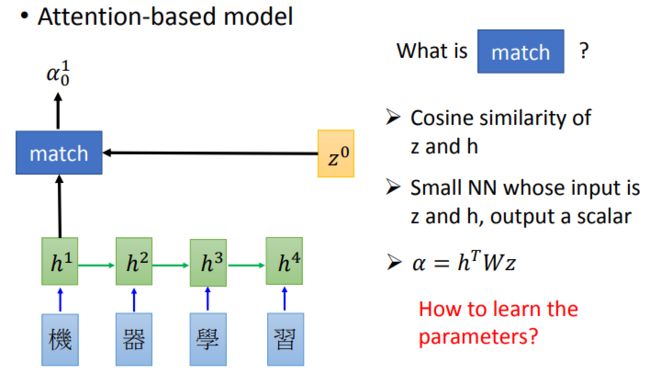
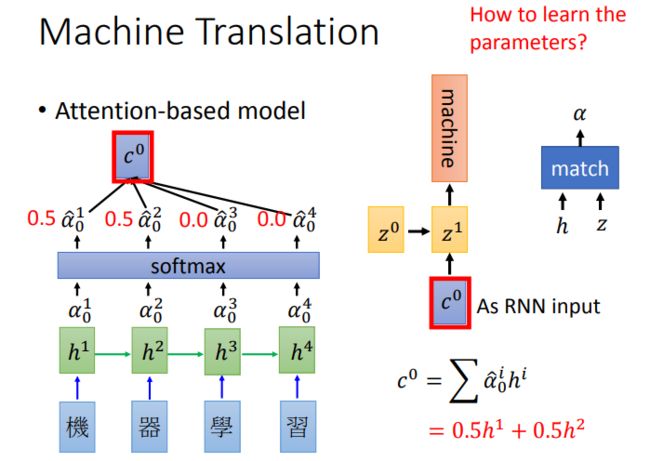
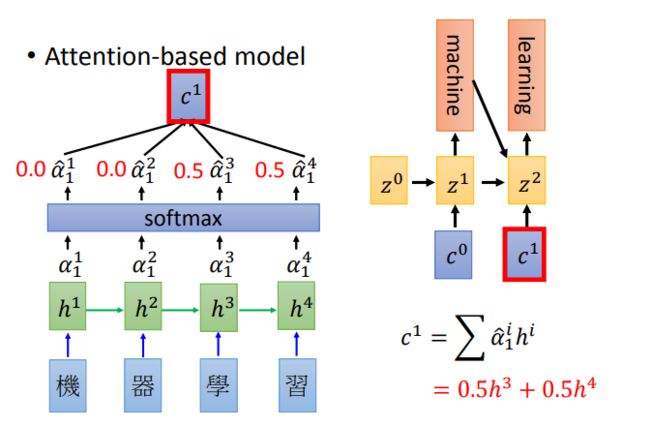
具体做法是：首先为编码器的每个输出关联一个分数，这个分数由解码器t-1时刻的网络状态和每个编码器输出的点乘积得到，然后用softmax层对这些关联分数进行归一化。最后，在加入到串联操作之前，利用归一化后的分数分别度量编码器的输出。这个策略的关键点是，编码器的每个输出计算得到的关联分数，表示了每个编码器输出对解码器t时刻决策的重要程度。

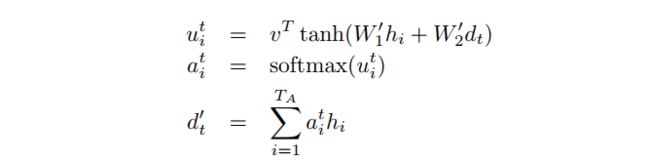
权重系数a思想就是根据当前解码“状态”判断输入序列的权重分布。

所谓的attention，就是在每个解码的时间步，对encoder的隐层状态进行加权求和，针对不同信息进行不同程度的注意力。

---

以上可以转化为如下机制：

输入是query(Q), key(K), value(V)，输出是attention value。如果与之前的模型对应起来的话，query就是$z_0,z_1$，key就是$h_1,h_2,h_3,h_4$，value也是$h_1,h_2,h_3,h_4$。模型通过Q和K的匹配计算出权重，再结合V得到输出：$$Attention(Q,K,V)=Softmax(sim(Q,K))V$$

注意力机制模仿了生物观察行为的内部过程，即一种将内部经验和外部感觉对齐从而增加部分区域的观察精细度的机制。注意力机制可以快速提取稀疏数据的重要特征，因而被广泛用于自然语言处理任务，特别是机器翻译。

而自注意力机制是注意力机制的改进，其减少了对外部信息的依赖，更擅长捕捉数据或特征的内部相关性。

---

词嵌入相关知识

---

正文

考虑到RNN（或者LSTM，GRU等）的计算限制为是顺序的，也就是说RNN相关算法只能从左向右依次计算或者从右向左依次计算，这种机制带来了两个问题：

1、时间片 t 的计算依赖 t-1 时刻的计算结果，这样限制了模型的并行能力；

2、顺序计算的过程中信息会丢失，尽管LSTM等门机制的结构一定程度上缓解了长期依赖的问题，但是对于特别长期的依赖现象,LSTM依旧无能为力。

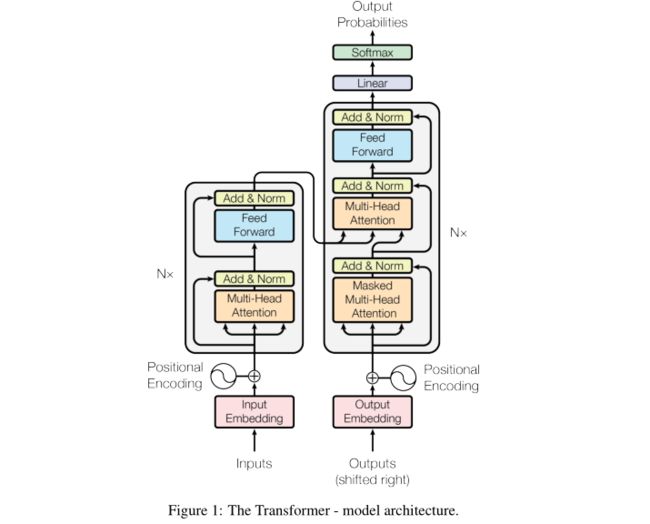
Architecture

Encoder

Encoder由N=6个相同的layer组成,每个Layer由两个sub-layer组成，分别是multi-head self-attention mechanism和fully connected feed-forward network。其中每个sub-layer都加了residual connection和normalisation，因此可以将sub-layer的输出表示为：LayerNorm(x + Sublayer(x))

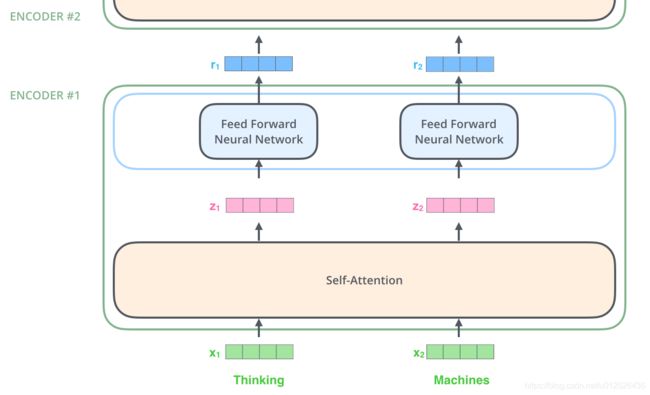
首先，模型需要对输入的数据进行一个embedding操作，也可以理解为类似w2c的操作，enmbedding结束之后，输入到encoder层，self-attention处理完数据后把数据送给前馈神经网络，前馈神经网络的计算可以并行，得到的输出会输入到下一个encoder。

self-attention

self-attention会计算出三个新的向量，在论文中，向量的维度是512维，我们把这三个向量分别称为Query、Key、Value，这三个向量是用embedding向量与一个矩阵相乘得到的结果，这个矩阵是随机初始化的，维度为（64，512）。注意第二个维度需要和embedding的维度一样，其值在BP的过程中会一直进行更新，得到的这三个向量的维度是64低于embedding维度的。

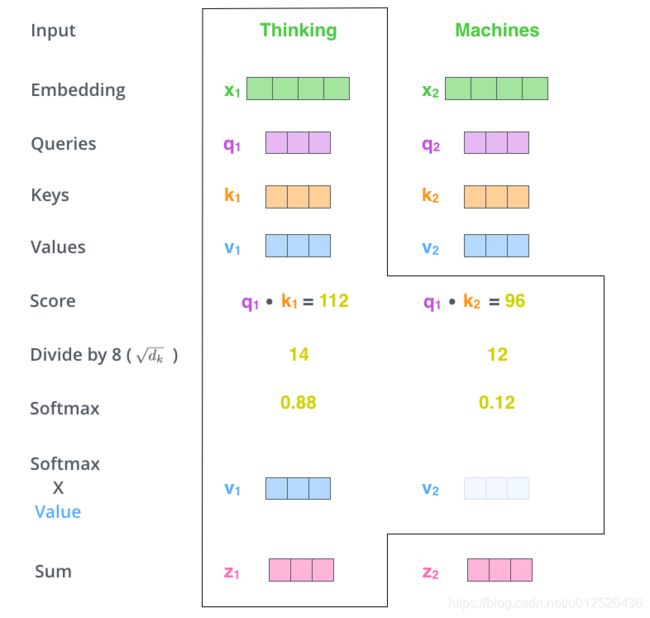
1.Scaled Dot-Product Attention

这种通过 query 和 key 的相似性程度来确定 value 的权重分布的方法被称为scaled dot-product attention。

2.Multi-head self-attention

不仅仅只初始化一组Q、K、V的矩阵，而是初始化多组，tranformer是使用了8组，所以最后得到的结果是8个矩阵。

multi-head attention则是通过h个不同的线性变换对Q，K，V进行投影，最后将不同的attention结果拼接起来：

self-attention则是Q，K，V来源相同，利用不同的矩阵随机初始化。

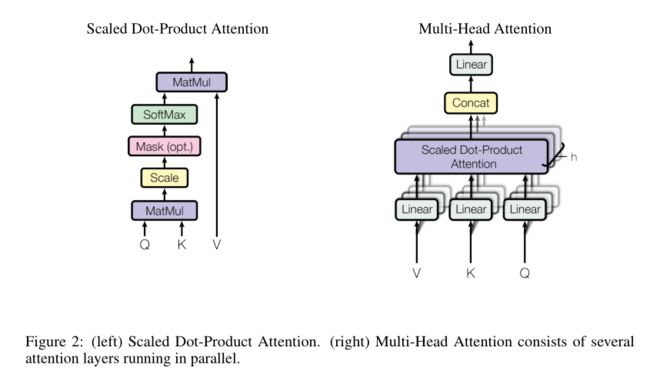
这就是multi-headed attention的全部流程了，这里其实已经有很多矩阵了，我们把所有的矩阵放到一张图内看一下总体的流程。

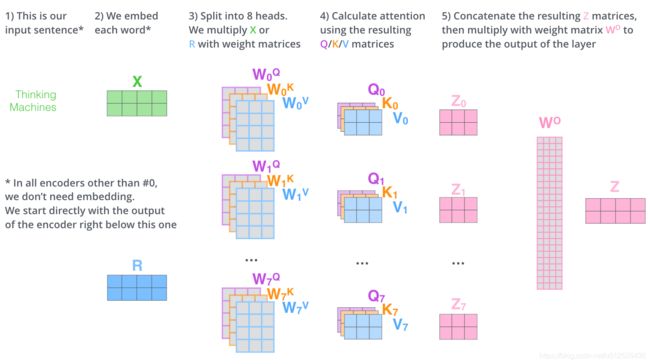
3.Position-wise Feed-Forward Networks

transformer模型中还缺少一种解释输入序列中单词顺序的方法。为了处理这个问题，transformer给encoder层和decoder层的输入添加了一个额外的向量Positional Encoding，维度和embedding的维度一样，这个向量采用了一种很独特的方法来让模型学习到这个值，这个向量能决定当前词的位置，或者说在一个句子中不同的词之间的距离。这个位置向量的具体计算方法有很多种，论文中的计算方法如下：

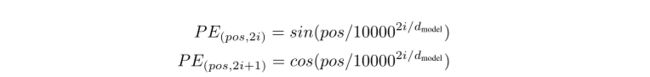
其中pos是指当前词在句子中的位置，i是指向量中每个值的index，可以看出，在偶数位置，使用正弦编码，在奇数位置，使用余弦编码。

考虑到在NLP任务中，除了单词的绝对位置，单词的相对位置也非常重要。根据公式 $sin(\alpha +\beta )=sin\alpha cos\beta +cos\alpha sin\beta$以及$cos(\alpha +\beta )=cos\alpha cos\beta -sin\alpha sin\beta$，这表明位置 k+p 的位置向量可以表示为位置 k 的特征向量的线性变化，这为模型捕捉单词之间的相对位置关系提供了非常大的便利。

最后把这个Positional Encoding与embedding的值相加，作为输入送到下一层。

一个是LayerNormalization（作用是把神经网络中隐藏层归一为标准正态分布，加速收敛），具体操作是将每一行的每一个元素减去这行的均值, 再除以这行的标准差, 从而得到归一化后的数值。

---

Decoder

输出：对应i位置的输出词的概率分布。

输入：encoder的输出 & 对应i-1位置decoder的输出（所以最开始的attention是self-attention(QKV全是decoder隐层)；中间的attention不是self-attention，K，V来自encoder，Q来自上一位置decoder的输出）。

解码：编码可以并行计算，一次性全部encoding出来，但解码不是一次把所有序列解出来的，而是像rnn一样一个一个解出来的，因为要用上一个位置的输入当作attention的query。

---

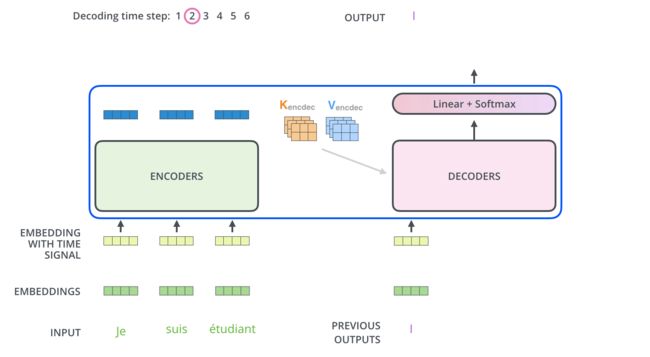
Code

class TransformerBlock(nn.Module):
    """
    Bidirectional Encoder = Transformer (self-attention)
    Transformer = MultiHead_Attention + Feed_Forward with sublayer connection
    """

    def __init__(self, hidden, attn_heads, feed_forward_hidden, dropout):
        """
        :param hidden: hidden size of transformer
        :param attn_heads: head sizes of multi-head attention
        :param feed_forward_hidden: feed_forward_hidden, usually 4*hidden_size
        :param dropout: dropout rate
        """

        super(TransformerBlock,self).__init__()
        self.attention = MultiHeadedAttention(h=attn_heads, d_model=hidden)
        self.feed_forward = PositionwiseFeedForward(d_model=hidden, d_ff=feed_forward_hidden, dropout=dropout)
        self.input_sublayer = SublayerConnection(size=hidden, dropout=dropout)
        self.output_sublayer = SublayerConnection(size=hidden, dropout=dropout)
        self.dropout = nn.Dropout(p=dropout)

    def forward(self, x, mask):
        x = self.input_sublayer(x, lambda x: self.attention.forward(x, x, x, mask=mask))
        x = self.output_sublayer(x, self.feed_forward)
        return self.dropout(x)

class PositionwiseFeedForward(nn.Module):
    "Implements FFN equation."

    def __init__(self, d_model, d_ff, dropout=0.1):
        super(PositionwiseFeedForward, self).__init__()
        self.w_1 = nn.Linear(d_model, d_ff)
        self.w_2 = nn.Linear(d_ff, d_model)
        self.dropout = nn.Dropout(dropout)
        self.activation = GELU()

    def forward(self, x):
        return self.w_2(self.dropout(self.activation(self.w_1(x))))

class MultiHeadedAttention(nn.Module):
    """
    Take in model size and number of heads.
    """

    def __init__(self, h, d_model, dropout=0.1):
        super().__init__()
        assert d_model % h == 0

        # We assume d_v always equals d_k
        self.d_k = d_model // h
        self.h = h

        self.linear_layers = nn.ModuleList([nn.Linear(d_model, d_model) for _ in range(3)])
        self.output_linear = nn.Linear(d_model, d_model)
        self.attention = Attention()

        self.dropout = nn.Dropout(p=dropout)

    def forward(self, query, key, value, mask=None):
        batch_size = query.size(0)

        # 1) Do all the linear projections in batch from d_model => h x d_k
        query, key, value = [l(x).view(batch_size, -1, self.h, self.d_k).transpose(1, 2)
                             for l, x in zip(self.linear_layers, (query, key, value))]

        # 2) Apply attention on all the projected vectors in batch.
        x, attn = self.attention(query, key, value, mask=mask, dropout=self.dropout)

        # 3) "Concat" using a view and apply a final linear.
        x = x.transpose(1, 2).contiguous().view(batch_size, -1, self.h * self.d_k)

        return self.output_linear(x)

class SublayerConnection(nn.Module):
    """
    A residual connection followed by a layer norm.
    Note for code simplicity the norm is first as opposed to last.
    """

    def __init__(self, size, dropout):
        super(SublayerConnection, self).__init__()
        self.norm = LayerNorm(size)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x, sublayer):
        "Apply residual connection to any sublayer with the same size."
        return x + self.dropout(sublayer(self.norm(x)))

class LayerNorm(nn.Module):
    "Construct a layernorm module (See citation for details)."

    def __init__(self, features, eps=1e-6):
        super(LayerNorm, self).__init__()
        self.a_2 = nn.Parameter(torch.ones(features))
        self.b_2 = nn.Parameter(torch.zeros(features))
        self.eps = eps

    def forward(self, x):
        mean = x.mean(-1, keepdim=True)
        std = x.std(-1, keepdim=True)
        return self.a_2 * (x - mean) / (std + self.eps) + self.b_2

class Attention(nn.Module):
    """
    Compute 'Scaled Dot Product Attention
    """

    def forward(self, query, key, value, mask=None, dropout=None):
        scores = torch.matmul(query, key.transpose(-2, -1)) \
                 / math.sqrt(query.size(-1))

        if mask is not None:
            scores = scores.masked_fill(mask == 0, -1e9)

        p_attn = F.softmax(scores, dim=-1)

        if dropout is not None:
            p_attn = dropout(p_attn)

        return torch.matmul(p_attn, value), p_attn