tensorflow_quantum 量子位的探讨!量子门的一些基本使用!基于TensorFlow_quantum的mnist分类!
文章目录
- 一、tensorflow_quantum 量子位的探讨
- 二、一些基础门的使用
-
- 一、X门(经典逻辑里面的非门)
- 二、H门(把量子位变成混合态)
- 三、基于TensorFlow_quantum mnist 分类
- 四、基于TensorFlow_quantum mnist 分类的其他想法
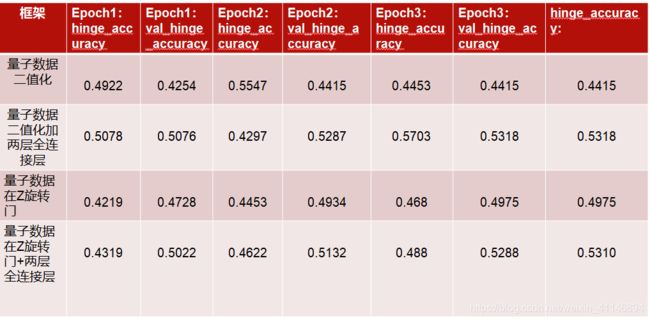
- 五、最后,结果对比图:
环境:安装tensorflow 2.1.0版本,最稳定
一、tensorflow_quantum 量子位的探讨
由于需要学习基于TensorFlow_quantum库,把量子卷积层和经典的深度学习相结合,这里介绍一下,cirq和量子门的一些基础知识,和容易想不通的几点小知识。自己也是初学者,相当于自己做笔记。
我们容易知道量子计算里面的基本状态是: (0,1),(1,0)。类似于经典计算机里面的二进制:0,1。
在学习tensorflow_quantum中,发现常常使用定义量子位是这样的语句:
q0, q1 = cirq.GridQubit.rect(1, 2)
qubits = cirq.GridQubit.rect(4, 4)
q3 = cirq.GridQubit(0,0)
那么这样定义是什么意思了?
我们首先不定义门,直接测量我们定义的量子位(cirq.GridQubit.rect(4, 4)):
import cirq
qubit3 = cirq.GridQubit.rect(4, 4)
# creates an equal superposition of |0> and |1> when simulated
# cirq.Z:Z旋转门,cirq.measure:测量
for i in range(16):
circuit = cirq.Circuit(cirq.Z(qubit3[i]),cirq.measure(qubit3[i]))
# see the "myqubit" identifier at the left of the circuit
print(circuit)
# run simulation
result = cirq.Simulator().simulate(circuit)
print("result:")
print(result)
运行结果:
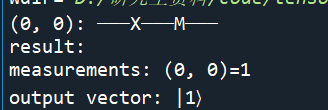
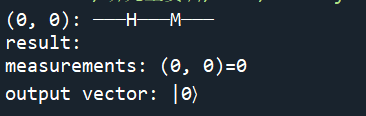
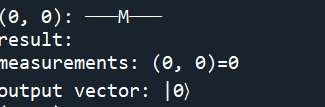
第一行:电路图(M是测量门)
第二行:结果
第三行:测量结果(应该是矢量)
第四行:输出矢量

很容易知道,qubit3 = cirq.GridQubit.rect(4, 4)相当于定义了一个二维矩阵,其中的(0,0),(0,1)…(3,3)’对应使我们的索引号(就是二维坐标对标的行和列数),每一个量子位初始化都为|0⟩=(1,0)。
这也是谷歌开发的库TensorFlow_quantum常用的一种量子位使用形式。
然后再来看看定义为q3 = cirq.GridQubit(0,0),打印结果我们容易知道:
在定义q3 = cirq.GridQubit(4,4)

这里相当于单独定义了一个量子位(0,0),(4,4)索引号,初始状态也是|0⟩=(1,0)。
所以说tensorflow_quantum定义的量子位初始状态都是|0⟩=(1,0)
二、一些基础门的使用
代码
import cirq
qubit = cirq.NamedQubit("myqubit")
qubit1 = cirq.NamedQubit("myqubit")
qubit3 = cirq.GridQubit.rect(4, 4)
qubit4 = cirq.GridQubit(0, 0)
# creates an equal superposition of |0> and |1> when simulated
# for i in range(16):
circuit = cirq.Circuit(cirq.H(qubit4),cirq.measure(qubit4))
# circuit = cirq.Circuit(cirq.X(qubit4),cirq.measure(qubit4))
# see the "myqubit" identifier at the left of the circuit
print(circuit)
# run simulation
result = cirq.Simulator().simulate(circuit)
print("result:")
print(result)
一、X门(经典逻辑里面的非门)
二、H门(把量子位变成混合态)
三、基于TensorFlow_quantum mnist 分类
这里只说一下关键点,具体实现思路可以去看官网教程
网站:https://tensorflow.google.cn/quantum/tutorials/mnist
它首先把4x4的数据集二值化,这个时候数据集就只有两个状态。

然后定义了4x4的量子位,用的是qubits = cirq.GridQubit.rect(4, 4)来定义的,我们前面可以知道,这个时候量子位的初始状态都是|0⟩=(1,0)。为了把对于1的像素点转化成对应的量子数据,这里他使用的是一个X门,进行旋转一下,这样量子数据对应的像素点就分开了。
然后就可以开始训练了。
由于本人的电脑性能有限,这里是训练集100张照片,测试集1968张照片的结果:

四、基于TensorFlow_quantum mnist 分类的其他想法
其实mnist还有很长想法可以实现:
比如说:不用将像素二值化,直接利用旋转门RX(),RZ(),RY()旋转的角度不同来代表像素点的大小,旋转的大小对应于像素点的大小,量子网络的神经网络框架不变(官方教程框架),直接修改对应函数部分即可,运行了四次正确率有所提高。
def convert_to_circuit(image):
"""Encode truncated classical image into quantum datapoint."""
values = np.ndarray.flatten(image)
qubits = cirq.GridQubit.rect(4, 4)
circuit = cirq.Circuit()
for i, value in enumerate(values):
if value:
circuit.append(cirq.rx(value).on(qubits[i]))
return circuit
结果:

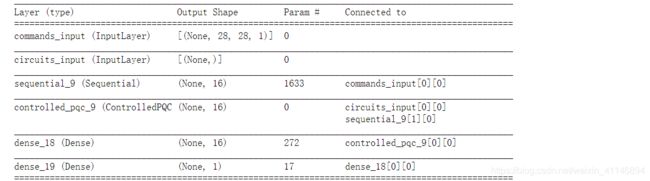
还有就是可以利用经典的神经网络框架,在网络框架的末尾加上量子神经网络,最后加上两层全连接神经网络,
详细代码如下:
import tensorflow as tf
import tensorflow_quantum as tfq
import cirq
import sympy
import numpy as np
import seaborn as sns
import collections
# visualization tools
%matplotlib inline
import matplotlib.pyplot as plt
from cirq.contrib.svg import SVGCircuit
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
print("Number of original training examples:", len(x_train))
print("Number of original test examples:", len(x_test))
def filter_36(x, y):
keep = (y == 3) | (y == 6)
x, y = x[keep], y[keep]
y = y == 3
return x,y
x_train, y_train = filter_36(x_train, y_train)
x_test, y_test = filter_36(x_test, y_test)
print(y_test.shape)
control_params = sympy.symbols('theta_1 theta_2 theta_3 theta_4 theta_5 theta_6 theta_7 theta_8 theta_9 theta_10 theta_11 theta_12 theta_13 theta_14 theta_15 theta_16')
qubit = cirq.GridQubit.rect(4, 4)
model_circuit = cirq.Circuit()
for i in range(16):
model_circuit.append(cirq.rz(control_params[i])(qubit[i]))
readouts = [cirq.Z(bit) for bit in qubit]
SVGCircuit(model_circuit)
# controller = tf.keras.Sequential([
# tf.keras.layers.Dense(10, activation='relu'),
# tf.keras.layers.Dense(16)
# ])
model = tf.keras.models.Sequential()
model.add(tf.keras.layers.Conv2D(32,kernel_size = [5,5],activation='relu',input_shape=(28,28,1)))
model.add(tf.keras.layers.MaxPooling2D([2,2]))
model.add(tf.keras.layers.Conv2D(1,kernel_size = [5,5],activation='relu'))
model.add(tf.keras.layers.MaxPooling2D([2,2]))
model.add(tf.keras.layers.Flatten())
controller = model
circuits_input = tf.keras.Input(shape=(),
# The circuit-tensor has dtype `tf.string`
dtype=tf.string,
name='circuits_input')
# Commands will be either `0` or `1`, specifying the state to set the qubit to.
commands_input = tf.keras.Input(shape=(28,28,1),
dtype=tf.dtypes.float32,
name='commands_input')
dense_2 = controller(commands_input)
expectation_layer = tfq.layers.ControlledPQC(model_circuit,
# Observe Z
operators = readouts)
expectation = expectation_layer([circuits_input, dense_2])
d1_dual = tf.keras.layers.Dense(16)(expectation)
d2_dual = tf.keras.layers.Dense(1)(d1_dual)
model = tf.keras.Model(inputs=[circuits_input, commands_input],
outputs=[d2_dual])
print(model.summary())
y_train_hinge = 2.0*y_train-1.0
y_test_hinge = 2.0*y_test-1.0
def hinge_accuracy(y_true, y_pred):
y_true = tf.squeeze(y_true) > 0.0
y_pred = tf.squeeze(y_pred) > 0.0
result = tf.cast(y_true == y_pred, tf.float32)
return tf.reduce_mean(result)
model.compile(
loss=tf.keras.losses.Hinge(),
optimizer=tf.keras.optimizers.Adam(),
metrics=[hinge_accuracy])
random_rotations = np.random.uniform(0, 2 * np.pi, 3)
noisy_preparation = cirq.Circuit()
np.random.seed(5)
for i in range(16):
noisy_preparation.append(cirq.Circuit(
cirq.rx(random_rotations[0])(qubit[i]),
cirq.ry(random_rotations[1])(qubit[i]),
cirq.rz(random_rotations[2])(qubit[i])
))
datapoint_circuits = tfq.convert_to_tensor([
noisy_preparation
] * 100)
datapoint_circuits_1= tfq.convert_to_tensor([
noisy_preparation
] * 1968)
EPOCHS = 10
BATCH_SIZE = 32
NUM_EXAMPLES = 100
x_train_tfcirc_sub = x_train[:NUM_EXAMPLES]
y_train_hinge_sub = y_train[:NUM_EXAMPLES]
qnn_history = model.fit(
x = [datapoint_circuits,x_train_tfcirc_sub.reshape(100,28,28,1)], y = y_train_hinge_sub,
batch_size=32,
epochs=EPOCHS,
validation_data=([datapoint_circuits_1,x_test.reshape(1968,28,28,1)], y_test_hinge)
)