【深度学习】如何构建一个超快速语义分割Transformer方案？丢掉多头机制！百度开源RTFormer（NeurIPS22）...

作者丨happy

编辑丨极市平台

导读

 

对于实时语义分割，由于 Transformer 的计算机制耗时，纯基于 CNN 的方法在该领域仍然占主导地位。本文提出了 RTFormer，一种用于实时语义分割的高效双分辨率转换器，与基于 CNN 的模型相比，它在性能和效率之间取得了更好的平衡。

论文链接：https://arxiv.org/abs/2210.07124 [NeurIPS2022]

代码地址：https://github.com/PaddlePaddle/PaddleSeg

尽管Transformer方案在语义分割领域取得了非常惊人的性能，但在实时性方面，纯CNN方案仍占据主流地位。本文提出了一种用于实时语义分割的高效对偶分辨率Transformer方案RTFormer，它具有比CNN方案更佳的性能-效率均衡。

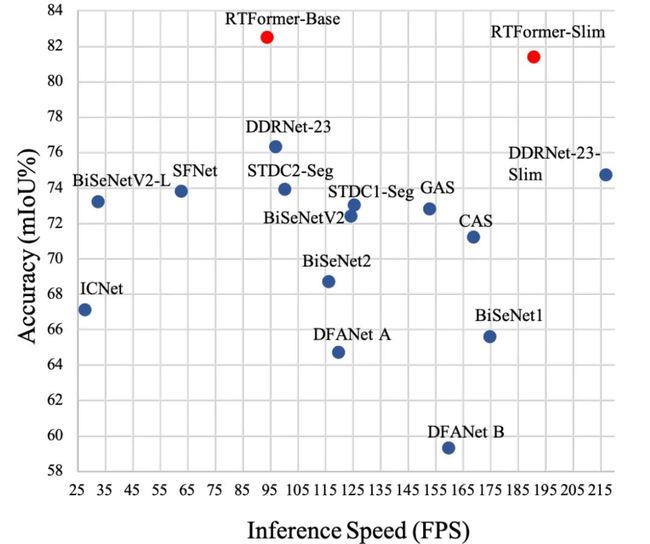
为达成GPU设备上的高推理效率，所提RTFormer采用了线性复杂度的GPU友好注意力模块，同时消除了多头机制。此外，作者发现：跨注意力机制对于全局上下文信息聚合非常有效。多个主流基准数据集(Cityscapes, CamVid, COCOStuff, ADE20K)上的实验结果验证了所提RTFormer的有效性。下图给出了CAMVid数据集上不同方案的性能与推理速度对比，很明显：RTFormer具有最佳的性能-速度均衡。

出发点

ViT技术在CV领域证实其有效性后，相关技术迅速在各个领域取得了一系列的成果。比如语义分割领域的DPT、SegFormer、HRFormer、Segmentor等均取得了非常优异的成绩。但是，相比CNN方案，Transformer方案因自注意力机制问题存在高计算量、高显存占用问题，导致其推理效率明显不如CNN方案。

作者认为：注意力机制在推理效率方面的瓶颈主要源自以下两个维度：

• 现有注意力机制的计算属性对于GPU设备不够友好，如二次复杂度、多头机制；

• 仅在高分辨率特征图实施注意力可能并非最有效捕获长距离上下文关系的方案，这是因为高分辨率特征的单个特征向量的感受野非常有限。

基于上述所提到的两个局限性，本文提出了一种GPU友好的注意力模块与跨分辨率注意力模块，并由此构建了RTFormer。

本文方案    

接下来，我们首先对本文所提GPU友好注意力RTFormer模块进行介绍，然后结合如何基于RTFormer模块构建RTFormer分割架构。

RTFormer block

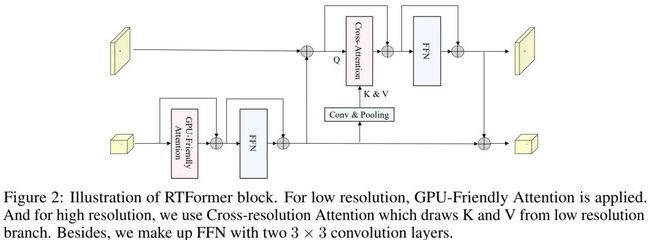
上图给出了本文所提RTFormer模块示意图，它是一种对偶分辨率模块，它包含两种类型注意力模块。在低分辨率分支，作者采用了GPU友好的注意力模块以捕获高层全局上下文信息，而在高分辨率分支，作者则引入了跨分辨率注意力机制对高层全局上下文信息进行传播扩散，也就是将两个分辨率的特征通过注意力模块进行聚合。

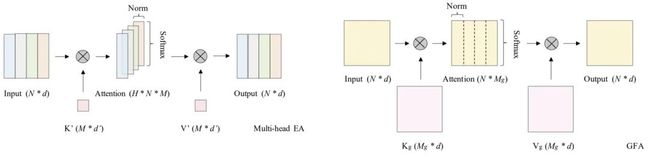
GPU-Friendly Attention  相比其他类型的注意力，作者发现：External Attention(EA，见上图左)因其线性复杂度可成为GPU设备的潜在选择。基于此，作者提出了GPU-Friendly Attention(GFA，见上图右)。我们首先对EA进行简要介绍，假设表示输入特征，那么EA可以描述如下：

其中，表示可学习参数，M表示参数维度，DN表示Double Normalization。多头版EA可描述如下：

尽管EA采用共享K与V，可以一定程度加速计算，但Splitted机制仍存在。为避免多头机制在GPU设备上的延迟问题，作者提出了一种简单而有效的GPU友好注意力，它在EA的基础上演变而来，表示如下：

其中，GDN表示分组DN。对比GFA与MHEA可以发现GFA有两个主要改进：

• 它使得矩阵乘操作成为一体且非常适合于GPU设备；

• 它在某种程度上了保持了多头机制的优势。

Cross-resolution Attention  已有研究证实：多分辨率融合对于稠密预测任务非常有效。对于多分辨率架构设计，我们在不同分支独立执行GAF处理，然后再进行信息交互。作者认为：直接在高分辨率特征执行注意力对于全局上下文学习不够高效。为更有效的获得全局上下文信息，作者提出了跨分辨率注意力，它可以充分利用从低分辨率分支学到的高层语义信息。该过程可描述如下：

需要注意的是：考虑到GPU设备的快速推理因素，这里同样消除了多头机制。

Feed Forward Network  SegFormer与HRFormer中的FFN由两个MLP层与深度卷积构成。但是，这种FFN对于GPU设备不够高效。为平衡性能与效率，作者在FFN中采用了两个卷积且不进行通道维度扩展。

RTFormer

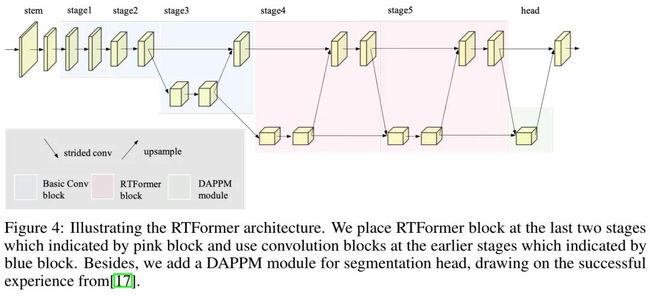
上图给出了RTFormer架构示意图，它由Backbone与SegHead两部分构成：

• Backbone：为提取高分辨率特征所需的局部信息，作者将卷积与所提RTFormer模块进行了组合以构建RTFormer。具体来说，RTFormer的Stem、Stage1以及Stage2部分由卷积与残差模块构成，从Stage3开始采用所提对偶分辨率模块以促进高分辨率分支与低分辨率分支特征的信息交互，在后三个阶段，高分辨率特征的stride保持为8不变，而低分辨率的stride则分别为16、32、32。值得说明的是，Stage分与Stage5由本文所提RTFormer模块构成以促进高效全局上下文建模，而Stage3则仍由残差模块构建。

• SegHead：在该部分，作者引入了DAPPM以进一步提取多尺度特征，此时输出特征的stride=8。最后，输出特征将被送入像素分类头(该分类头由卷积与卷积构成)以进行稠密语义标签。

上表给出了RTFormer-Slim与RTFormer-Base的架构配置信息，很明显，RTFormer的骨干部分由5个stage构成，其中3-5stage由对偶分辨率特征构成，在分割头方面，RTFormer引入了DPPM模块进一步提取多尺度特征。

本文实验

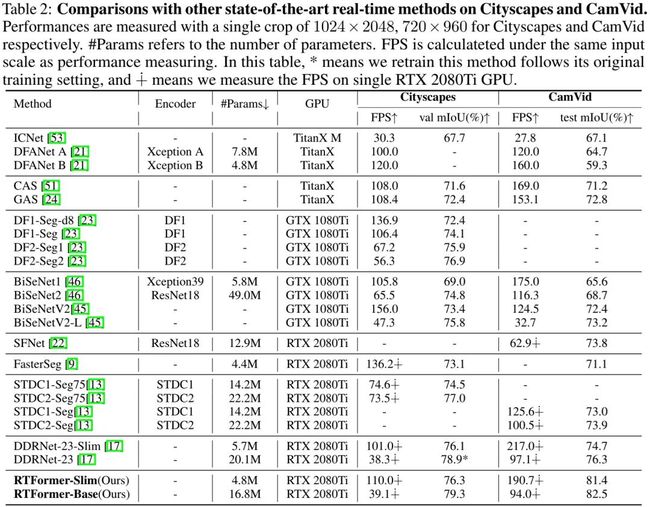
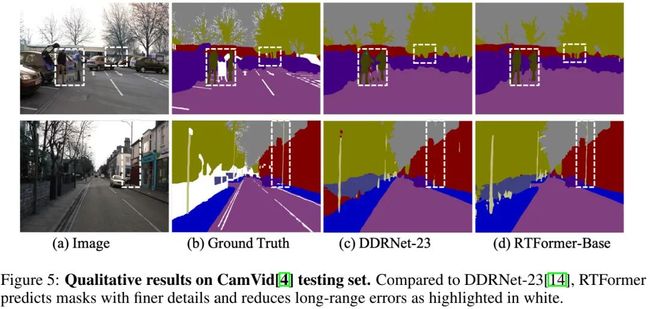
上表与图给出了Cityscapes与CamVid数据集上的性能对比，从中可以看到：

• 在Cityscapes数据集上，在所有实时分割方案中，RTFormer取得了最佳的速度-精度均衡；

• RTFormer-Slim取得了76.3%mIoU指标且推理速度高达110.0FPS，优于STDC2-Seg75与DDRNet-23-Slim。

• RTFormer-Base取得了79.3%mIoU指标且推理速度高达39.1FPS，取得了新的SOTA结果。

• 在CamVid数据集上，所提方案仅需ImageNet预训练即取得了82.5%mIoU指标且推理速度达94.FPS，优于采用额外Cityscapes预训练的STDC2-Seg；

• RTFormer-Slim仅需4.8M参数即取得了81.4mIoU指标且推理速度高达190.7FPS，优于STDC2-Seg与DDRNet-23；

• 从视觉效果方面来看，RTFormer-Base具有更佳的细粒度分解结果。

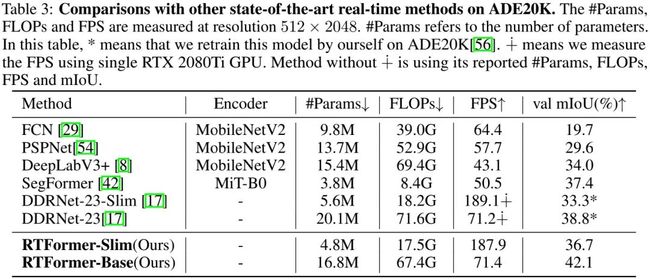
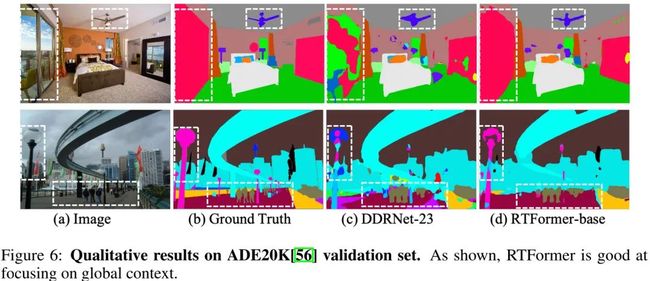
上表与图给出了ADE20K数据集上不同方案的性能对比，从中可以看到：

• RTFormer-Base取得了42.1%mIoU指标且推理速度达71.4FPS，优于其他方案；

• 相比DDRNet-23-Slim，RTFormer-SLim取得了36.7%mIoU指标，同时保持相当的速度。

• 从视觉效果可以看到：相比DDRNet-23，所提方案的分割结果具有更好的细节与上下文信息。

Code解析

本文代码已经开源在PaddleSeg仓库，笔者对其核心code进行摘录如下：

class RTFormer(nn.Layer):
    def __init__(self, ...):
        super().__init__()
        ...
    def forward(self, x):
        x1 = self.layer1(self.conv1(x))
        x2 = self.layer2(self.relu(x1))
        
        # stage-3
        x3 = self.layer3(self.relu(x2))
        x3_ = x2 + F.interpolate(self.compression3(x3), size=paddle.shape(x2)[2:], mode='bilienar')
        x3_ = self.layer3_(self.relu(x3_))
        
        # stage-4与stage-5的计算流程类似stage-3
        x4_ = ...
        x5_ = ...
        
        # SegHead, DAPPM
        x6 = self.spp(x5)
        x6 = x6 + F.interpolate(x6, size=paddle.shape(x5_), mode='bilinear')
        x_out = self.seghead(paddle.concat([x5_, x6], axis=1))
        return F.interpolate(x_out, paddle.shape(x)[2:], mode='bilinear')


class ExternalAttention(nn.Layer):
   def __init__(self, ...)
       super().__init__()
       
   def _act_sn(self, x):
       x = x.reshape([-1, self.inter_channels, 0, 0]) * (self.inter_channels ** -0.5)
       x = F.softmax(x, axis=1)
       x = x.reshape([1, -1, 0, 0])
   def _act_dn(self, x):
       x_shape = paddle.shape(x)
       h, w = x_shape[2], x_shape[3]
       x = x.reshape([0, self.num_heads, self.inter_channels //self.num_heads, -1])
       x = F.softmax(x, axis=3)
       x = x / (paddle.sum(x, axis=2, keepdim=True) + 1e-06)
       x = x.reshape([0, self.inter_channels, h, w])
       
   def forward(self, x, cross_k=None, cross_v=None):
       x = self.norm(x)
       if not self.use_cross_kv:
           x = F.conv2d(x, self.k, bias=None, stride=2 if not self.same_in_out_chs else 1, padding=0) 
           x = self._act_dn(x)  # n,c_inter,h,w
           x = F.conv2d(x, self.v, bias=None, stride=1, padding=0)
        else:
           B = x.shape[0]
           x = x.reshape([1, -1, 0, 0])  # n,c_in,h,w -> 1,n*c_in,h,w
           x = F.conv2d(x, cross_k, bias=None, stride=1, padding=0, groups=B)  
           x = self._act_sn(x)
           x = F.conv2d(x, cross_v, bias=None, stride=1, padding=0, groups=B)  
           x = x.reshape([-1, self.in_channels, 0, 0]) 
        return x

往期精彩回顾




适合初学者入门人工智能的路线及资料下载(图文+视频)机器学习入门系列下载机器学习及深度学习笔记等资料打印《统计学习方法》的代码复现专辑机器学习交流qq群955171419，加入微信群请扫码