sklearn学习DBSCAN聚类
原文链接
1. sklearn中的DBSCAN类
\qquad 在sklearn中,DBSCAN算法(Density-Based Spatial Clustering of Applications with Noise,具有噪声的基于密度的聚类方法)类为sklearn.cluster.DBSCAN。要熟练的掌握用DBSCAN类来聚类,除了对DBSCAN本身的原理有较深的理解以外,还要对最近邻的思想有一定的理解。集合这两者,就可以玩转DBSCAN了。
2. DBSCAN类重要参数
\qquad DBSCAN类的重要参数也分为两类,一类是DBSCAN算法本身的参数,一类是最近邻度量的参数,下面我们对这些参数做一个总结。
\qquad 1)eps: DBSCAN算法参数,即我们的 ϵ \epsilon ϵ-邻域的距离阈值,和样本距离超过 ϵ \epsilon ϵ的样本点不在 ϵ \epsilon ϵ-邻域内。默认值是0.5。一般需要通过在多组值里面选择一个合适的阈值。eps过大,则更多的点会落在核心对象的 ϵ \epsilon ϵ-邻域,此时我们的类别数可能会减少, 本来不应该是一类的样本也会被划为一类。反之则类别数可能会增大,本来是一类的样本却被划分开。
\qquad 2)min_samples: DBSCAN算法参数,即样本点要成为核心对象所需要的 ϵ \epsilon ϵ-邻域的样本数阈值。默认值是5。 一般需要通过在多组值里面选择一个合适的阈值。通常和eps一起调参。在eps一定的情况下,min_samples过大,则核心对象会过少,此时簇内部分本来是一类的样本可能会被标为噪音点,类别数也会变多。反之min_samples过小的话,则会产生大量的核心对象,可能会导致类别数过少。
\qquad 3)metric:最近邻距离度量参数。可以使用的距离度量较多,一般来说DBSCAN使用默认的欧式距离(即p=2的闵可夫斯基距离)就可以满足我们的需求。可以使用的距离度量参数有:
\qquad a) 欧式距离 “euclidean”: ∑ i = 1 n ( x i − y i ) 2 \sqrt{\sum\limits_{i=1}^n(x_i-y_i)^2} i=1∑n(xi−yi)2
\qquad b) 曼哈顿距离"manhattan": ∑ i = 1 n ∣ x i − y i ∣ \sum\limits_{i=1}^n|x_i-y_i| i=1∑n∣xi−yi∣
\qquad c) 切比雪夫距离"chebyshev": m a x ∣ x i − y i ∣ ( i = 1 , 2 , … , n ) max{|x_i-y_i|} (i=1,2,\dots,n) max∣xi−yi∣(i=1,2,…,n)
\qquad d) 闵可夫斯基距离 “minkowski”: ∑ i = 1 n ( ∣ x i − y i ∣ ) p p p = 1 \sqrt[p]{\sum\limits_{i=1}^n(|x_i-y_i|)^p} \ p=1 pi=1∑n(∣xi−yi∣)p p=1为曼哈顿距离, p = 2 p=2 p=2为欧式距离。
\qquad e) 带权重闵可夫斯基距离 “wminkowski”: ∑ i = 1 n ( w ∗ ∣ x i − y i ∣ ) p p \sqrt[p]{\sum\limits_{i=1}^n (w * |x_i-y_i|)^p} pi=1∑n(w∗∣xi−yi∣)p,其中 w w w为特征权重。
\qquad f) 标准化欧式距离 “seuclidean”: 即对于各特征维度做了归一化以后的欧式距离。此时各样本特征维度的均值为0,方差为1。
\qquad g) 马氏距离“mahalanobis”: ( x − y ) T S − 1 ( x − y ) \sqrt{(x-y)^TS^{-1}(x-y)} (x−y)TS−1(x−y),其中, S − 1 S^-1 S−1为样本协方差矩阵的逆矩阵。当样本分布独立时, S S S为单位矩阵,此时马氏距离等同于欧式距离。
\qquad 还有一些其他不是实数的距离度量,一般在DBSCAN算法用不上,这里也就不列了。
\qquad 4)algorithm:最近邻搜索算法参数,算法一共有三种,第一种是蛮力实现,第二种是KD树实现,第三种是球树实现。这三种方法与K近邻法(KNN)原理中算法一致。对于这个参数,一共有4种可选输入,‘brute’对应第一种蛮力实现,‘kd_tree’对应第二种KD树实现,‘ball_tree’对应第三种的球树实现, ‘auto’则会在上面三种算法中做权衡,选择一个拟合最好的最优算法。需要注意的是,如果输入样本特征是稀疏的时候,无论我们选择哪种算法,最后sklearn都会去用蛮力实现‘brute’。个人的经验,一般情况使用默认的 ‘auto’就够了。 如果数据量很大或者特征也很多,用"auto"建树时间可能会很长,效率不高,建议选择KD树实现‘kd_tree’,此时如果发现‘kd_tree’速度比较慢或者已经知道样本分布不是很均匀时,可以尝试用‘ball_tree’。
\qquad 5)leaf_size:最近邻搜索算法参数,为使用KD树或者球树时, 停止建子树的叶子节点数量的阈值。这个值越小,则生成的KD树或者球树就越大,层数越深,建树时间越长,反之,则生成的KD树或者球树会小,层数较浅,建树时间较短。默认是30。因为这个值一般只影响算法的运行速度和使用内存大小,因此一般情况下可以不管它。
\qquad 6) p: 最近邻距离度量参数。只用于闵可夫斯基距离和带权重闵可夫斯基距离中 p p p值的选择, p = 1 p=1 p=1为曼哈顿距离, p = 2 p=2 p=2为欧式距离。如果使用默认的欧式距离不需要管这个参数。
\qquad 以上就是DBSCAN类的主要参数介绍,其实需要调参的就是两个参数eps和min_samples,这两个值的组合对最终的聚类效果有很大的影响。
3. scikit-learn DBSCAN聚类实例
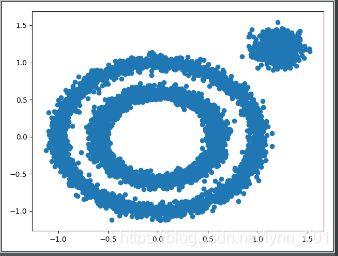
\qquad 首先,我们生成一组随机数据,为了体现DBSCAN在非凸数据的聚类优点,我们生成了三簇数据,两组是非凸的。代码如下:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles, make_blobs
X1, y1 = make_circles(n_samples=5000, factor=0.6, noise=0.05)
X2, y2 = make_blobs(n_samples=1000, n_features=2, centers=[[1.2, 1.2]], cluster_std=[[.1]], random_state=9)
X = np.r_[X1, X2]
plt.scatter(X[:, 0], X[:, 1], marker='o')
plt.show()
\qquad 首先我们看看K-Means的聚类效果,代码如下:
from sklearn.cluster import KMeans
y_pred = KMeans(n_clusters=3, random_state=9).fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()
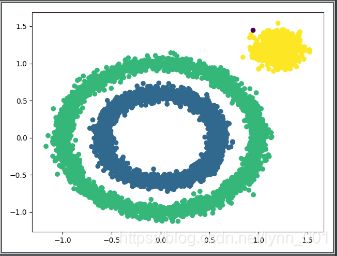
\qquad K-Means对于非凸数据集的聚类表现不好,从上面代码输出的聚类效果图可以明显看出。那么如果使用DBSCAN效果如何呢?我们先不调参,直接用默认参数,看看聚类效果,代码如下:
from sklearn.cluster import DBSCAN
y_pred = DBSCAN().fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()
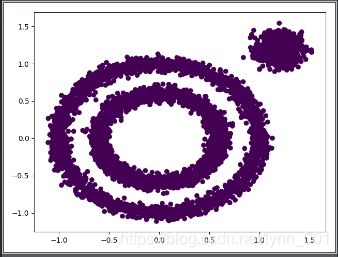
\qquad 发现输出让我们很不满意,DBSCAN居然认为所有的数据都是一类!我们需要对DBSCAN的两个关键的参数eps和min_samples进行调参!从上图我们可以发现,类别数太少,我们需要增加类别数,那么我们可以减少 ϵ \epsilon ϵ-邻域的大小,默认是0.5,我们减到0.2看看效果。代码如下:
y_pred = DBSCAN(eps=0.2).fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()
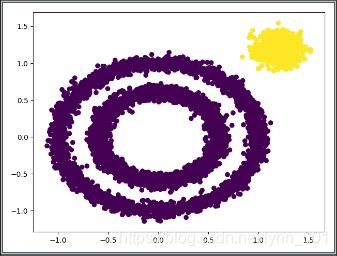
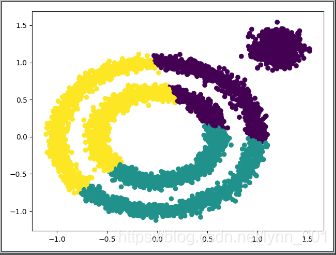
\qquad 可以看到聚类效果有了改进,至少边上的那个簇已经被发现出来了。此时我们需要继续调参增加类别,有两个方向都是可以的,一个是继续减少eps,另一个是增加min_samples。我们现在将eps减小到0.1,min_samples从默认的5增加到10,代码如下:
y_pred = DBSCAN(eps=0.1, min_samples=10).fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()