sklearn机器学习——day16
XGBoost的三大板块:集成算法本身,用于集成的 弱评估器,以及应用中的其他过程
梯度提升树
提升集成算法:重要参数n_estimators
集成算法通过在数据上构建多个弱 评估器,汇总所有弱评估器的建模结果,以获取比单个模型更好的回归或分类表现
进行一次简单的建模
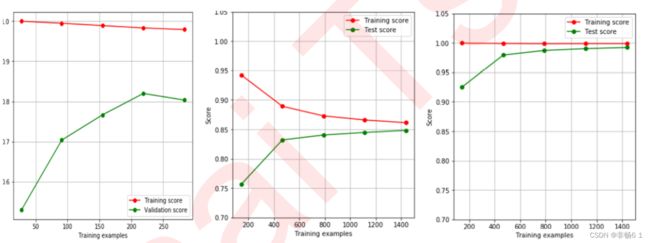
使用参数学习曲线观察n_estimators对模型的影响
#=====【TIME WARNING:25 seconds】=====#
axisx = range(10,1010,50)
rs = []
for i in axisx:
reg = XGBR(n_estimators=i,random_state=420)
rs.append(CVS(reg,Xtrain,Ytrain,cv=cv).mean())
print(axisx[rs.index(max(rs))],max(rs))
plt.figure(figsize=(20,5))
plt.plot(axisx,rs,c="red",label="XGB")
plt.legend()
plt.show()
#选出来的n_estimators非常不寻常,我们是否要选择准确率最高的n_estimators值呢?进化的学习曲线:方差与泛化误差
#======【TIME WARNING: 20s】=======#
axisx = range(50,1050,50)
rs = []
var = []
ge = []
for i in axisx:
reg = XGBR(n_estimators=i,random_state=420)
cvresult = CVS(reg,Xtrain,Ytrain,cv=cv)
#记录1-偏差
rs.append(cvresult.mean())
#记录方差
var.append(cvresult.var())
#计算泛化误差的可控部分
ge.append((1 - cvresult.mean())**2+cvresult.var())
#打印R2最高所对应的参数取值,并打印这个参数下的方差
print(axisx[rs.index(max(rs))],max(rs),var[rs.index(max(rs))])
#打印方差最低时对应的参数取值,并打印这个参数下的R2
print(axisx[var.index(min(var))],rs[var.index(min(var))],min(var))
#打印泛化误差可控部分的参数取值,并打印这个参数下的R2,方差以及泛化误差的可控部分
print(axisx[ge.index(min(ge))],rs[ge.index(min(ge))],var[ge.index(min(ge))],min(ge))
plt.figure(figsize=(20,5))
plt.plot(axisx,rs,c="red",label="XGB")
plt.legend()
plt.show()细化学习曲线,找出最佳n_estimators
axisx = range(100,300,10)
rs = []
var = []
ge = []
for i in axisx:
reg = XGBR(n_estimators=i,random_state=420)
cvresult = CVS(reg,Xtrain,Ytrain,cv=cv)
rs.append(cvresult.mean())
var.append(cvresult.var())
ge.append((1 - cvresult.mean())**2+cvresult.var())
print(axisx[rs.index(max(rs))],max(rs),var[rs.index(max(rs))])
print(axisx[var.index(min(var))],rs[var.index(min(var))],min(var))
print(axisx[ge.index(min(ge))],rs[ge.index(min(ge))],var[ge.index(min(ge))],min(ge))
rs = np.array(rs)
var = np.array(var)*0.01
plt.figure(figsize=(20,5))
plt.plot(axisx,rs,c="black",label="XGB")
#添加方差线
plt.plot(axisx,rs+var,c="red",linestyle='-.')
plt.plot(axisx,rs-var,c="red",linestyle='-.')
plt.legend()
plt.show()
#看看泛化误差的可控部分如何?
plt.figure(figsize=(20,5))
plt.plot(axisx,ge,c="gray",linestyle='-.')
plt.show()检测模型效果
#验证模型效果是否提高了?
time0 = time()
print(XGBR(n_estimators=100,random_state=420).fit(Xtrain,Ytrain).score(Xtest,Ytest))
print(time()-time0)
time0 = time()
print(XGBR(n_estimators=660,random_state=420).fit(Xtrain,Ytrain).score(Xtest,Ytest))
print(time()-time0)
time0 = time()
print(XGBR(n_estimators=180,random_state=420).fit(Xtrain,Ytrain).score(Xtest,Ytest))
print(time()-time0)有放回随机抽样:重要参数subsample
在这次的抽样 中,我们加大了被第一棵树判断错误的样本的权重
的subsample参数对模型的影响应该会非常不稳定,大概率应该是无法提升模型的泛化能力 的,但也不乏提升模型的可能性。依然使用波士顿房价数据集,来看学习曲线:
axisx = np.linspace(0,1,20)
rs = []
for i in axisx:
reg = XGBR(n_estimators=180,subsample=i,random_state=420)
rs.append(CVS(reg,Xtrain,Ytrain,cv=cv).mean())
print(axisx[rs.index(max(rs))],max(rs))
plt.figure(figsize=(20,5))
plt.plot(axisx,rs,c="green",label="XGB")
plt.legend()
plt.show()
#细化学习曲线
axisx = np.linspace(0.05,1,20)
rs = []
var = []
ge = []
for i in axisx:
reg = XGBR(n_estimators=180,subsample=i,random_state=420)
cvresult = CVS(reg,Xtrain,Ytrain,cv=cv)
rs.append(cvresult.mean())
var.append(cvresult.var())
ge.append((1 - cvresult.mean())**2+cvresult.var())
print(axisx[rs.index(max(rs))],max(rs),var[rs.index(max(rs))])
print(axisx[var.index(min(var))],rs[var.index(min(var))],min(var))
print(axisx[ge.index(min(ge))],rs[ge.index(min(ge))],var[ge.index(min(ge))],min(ge))
rs = np.array(rs)
var = np.array(var)
plt.figure(figsize=(20,5))
plt.plot(axisx,rs,c="black",label="XGB")
plt.plot(axisx,rs+var,c="red",linestyle='-.')
plt.plot(axisx,rs-var,c="red",linestyle='-.')
plt.legend()
plt.show()
#继续细化学习曲线
axisx = np.linspace(0.75,1,25)
#不要盲目找寻泛化误差可控部分的最低值,注意观察结果
#看看泛化误差的情况如何
reg = XGBR(n_estimators=180
,subsample=0.7708333333333334
,random_state=420).fit(Xtrain,Ytrain)
reg.score(Xtest,Ytest)
MSE(Ytest,reg.predict(Xtest))
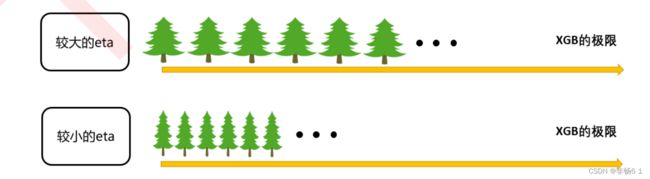
#这样的结果说明了什么?迭代决策树:重要参数eta
来探索一下参数eta的性质:
#首先我们先来定义一个评分函数,这个评分函数能够帮助我们直接打印Xtrain上的交叉验证结果
def regassess(reg,Xtrain,Ytrain,cv,scoring = ["r2"],show=True):
score = []
for i in range(len(scoring)):
if show:
print("{}:{:.2f}".format(scoring[i]
,CVS(reg
,Xtrain,Ytrain
,cv=cv,scoring=scoring[i]).mean()))
score.append(CVS(reg,Xtrain,Ytrain,cv=cv,scoring=scoring[i]).mean())
return score
#运行一下函数来看看效果
regassess(reg,Xtrain,Ytrain,cv,scoring = ["r2","neg_mean_squared_error"])
#关闭打印功能试试看?
regassess(reg,Xtrain,Ytrain,cv,scoring = ["r2","neg_mean_squared_error"],show=False)
#观察一下eta如何影响我们的模型:
from time import time
import datetime
for i in [0,0.2,0.5,1]:
time0=time()
reg = XGBR(n_estimators=180,random_state=420,learning_rate=i)
print("learning_rate = {}".format(i))
regassess(reg,Xtrain,Ytrain,cv,scoring = ["r2","neg_mean_squared_error"])
print(datetime.datetime.fromtimestamp(time()-time0).strftime("%M:%S:%f"))
print("\t")
axisx = np.arange(0.05,1,0.05)
rs = []
te = []
for i in axisx:
reg = XGBR(n_estimators=180,random_state=420,learning_rate=i)
score = regassess(reg,Xtrain,Ytrain,cv,scoring =
["r2","neg_mean_squared_error"],show=False)
test = reg.fit(Xtrain,Ytrain).score(Xtest,Ytest)
rs.append(score[0])
te.append(test)
print(axisx[rs.index(max(rs))],max(rs))
plt.figure(figsize=(20,5))
plt.plot(axisx,te,c="gray",label="XGB")
plt.plot(axisx,rs,c="green",label="XGB")
plt.legend()
plt.show()