【算法积累】一种改进的DBSCAN算法
一种改进的DBSCAN算法
1 前言
改进了传统的DBSCAN算法,算法的时间复杂度从 O ( n 2 ) O(n^2) O(n2)降低到了 O ( n + m ∗ k 2 ) O(n+m*k^2) O(n+m∗k2)
2 传统的DBSCAN算法
如下表所示,给出了一些关于DBSCAN算法的相关定义
 其中,密度可达可用以下公式表示
其中,密度可达可用以下公式表示

根据以上定义,DBSCAN的集群发现过程首先需要从数据集 D D D中找到一个点 p p p并对其进行检查。如果点 p p p是一个核心点,即点 p p p的 E p s Eps Eps邻域内的点个数大于等于 M i n P t s MinPts MinPts,那么在接下来的过程中,点 p p p的 E p s Eps Eps邻域内的点将依次被检查为种子点,即连续查询种子点。如果当前种子点也是核心点,则将其 E p s Eps Eps邻域内的点放入种子集。这样,当前类中的数据点就会被不断地扩展,直到找到一个完整的类。如果 p p p是一个边界点,这意味着点 p p p的 E p s Eps Eps邻域内的点数小于 M i n P t s MinPts MinPts,因此算法会选择数据集 D D D中的下一个点进行检查。其余未被划分成任何簇的点将被标记为噪声点。
3 改进的DBSCAN算法
改进的DBSCAN算法采用广度优先搜索连接多个网格单元,采用贪婪算法的增长模式形成聚类。
3.1 相关定义
以下为改进DBSCAN算法的一些定义:
定义1 :网格单元
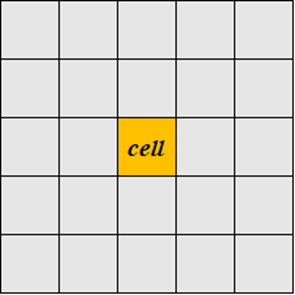
设置一个划分参数 ε \varepsilon ε,将每一个维度的数据空间划分为相同长度的区域,从而将整个二维数据空间划分若干个边长为 ε \varepsilon ε的网格单元。如果最后一个网格单元的边长小于 ε \varepsilon ε,但为了确保计算的准确性和一致性,我们仍设置最后一个网格单元的边长为 ε \varepsilon ε。下图中橙色的部分代表了一个网格单元。
定义2: k k k邻接网格集
c e l l cell cell是一个网格单元格。一个矩形区域可以通过在 c e l l cell cell的上下左右四个方向上加 k k k个边长(即 k ∗ ε k*\varepsilon k∗ε的长度)来扩展, k k k邻接网格集定义为该矩形区域所包含的网格集,用 N c e l l Ncell Ncell表示,如下图绿色区域所示,表示了定义1中 c e l l cell cell的1邻接网格集。

定义3: E p s Eps Eps矩形区域
c e l l cell cell是一个网格单元格。在 c e l l cell cell的4个顶点处画4个圆心,半径为 E p s Eps Eps。 c e l l cell cell的 E p s Eps Eps矩形区域定义为该区域由能够覆盖上述4个圆区域的 k k k邻接网格集组成。
3.2 改进DBSCAN算法的主要思想
将 c e l l cell cell的边长 L p g Lpg Lpg设为 E p s / p Eps/p Eps/p,便于根据上述定义计算 c e l l cell cell的 E p s Eps Eps矩形区域。显然, c e l l cell cell的 E p s Eps Eps矩形区域是由 c e l l cell cell的 p p p邻接网格集组成的区域。当 p ⩾ 1 p\geqslant 1 p⩾1时,矩形区域的边长为 ( 2 p + 1 ) ∗ L p g (2p+1)*Lpg (2p+1)∗Lpg;当 p < 1 p<1 p<1时, c e l l cell cell的 E p s Eps Eps矩形区域是由 c e l l cell cell的1邻接网格集组成的区域,边长为 3 ∗ L p g 3*Lpg 3∗Lpg。
c e l l cell cell中 p = 1 p=1 p=1的 E p s Eps Eps矩形区域如下图中蓝色区域所示。从图中可以看出,当 c e l l cell cell的 E p s Eps Eps矩形区域内的点数小于 M i n P t s MinPts MinPts时, c e l l cell cell中的任意一点都不可能是核心点。只需计算 c e l l cell cell中的种子点与 c e l l cell cell矩形区域内的点之间的距离,即可判断种子点是否为核心点。大大减少了点对点距离的计算。
1.将数据空间划分为几个网格单元
2.建立数据点到网格单元的映射关系
3.使用广度优先搜索生成集群。这一步表明搜索点 p p p的邻域范围正在缩小。具体程序如下:
a)将第一个(下一个)标记为未读的点放入队列中作为种子点,直到所有点都标记为已读再结束;
b)取队列头上的点来执行区域查询,并将该点标记为已读,如果队列为空,则执行步骤a);
c)如果在 E p s Eps Eps矩形区域内点的数量大于或等于 M i n P t s MinPts MinPts,然后测试 E p s Eps Eps矩形区域内的点到种子点的距离小于等于 E p s Eps Eps的点个数是否大于等于 M i n P t s MinPts MinPts,如果测试结果是真的,种子点是一个核心点,并将其 E p s Eps Eps邻近的点作为种子点放入队列中;如果测试结果是假的,将其恢复为未读。如果 E p s Eps Eps矩形区域内的点数小于 M i n P t s MinPts MinPts,立即将种子点恢复为未读;
d)重复执行步骤b),c)。
核心点的判断方法在上面有详细的介绍,利用欧几里德距离公式计算两个 t t t维空间点之间的距离,公式如下:
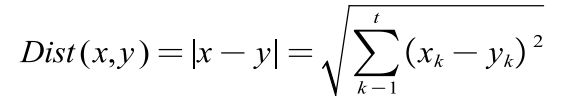
4 时间复杂度分析
4.1 DBSCAN
因为每次查询都返回该区域内的所有对象,时间复杂度为 O ( n 2 ) O(n^2) O(n2),因此DBSCAN算法的时间开销很大。此外,所有的数据都应该保存在内存中,它需要大的内存和大的I/O消耗。
4.2 改进的DBSCAN
本文提出的方法针对二维数据,算法包括3个步骤:
第1步,将数据空间划分为网格单元,需要计算每个维度数据空间的最大值和最小值,时间复杂度为 O ( n ) O(n) O(n);
第2步,算法在建立数据点到网格单元的映射关系时,需要遍历 n n n个数据集,因此时间复杂度为 O ( n ) O(n) O(n);
第3步,利用广度优先搜索生成集群,将种子点的检查线程化为广度优先搜索过程,时间复杂度为 O ( n + m e ) O(n+me) O(n+me)。 m m m为扩展点个数, e e e为计算格单元边长 L p g = E p s / p Lpg=Eps/p Lpg=Eps/p时,在 ( 2 k + 1 ) 2 (2k+1)^2 (2k+1)2个网格内计算点数 s s s并进行相应操作的时间,所以 e e e的时间复杂度是 O ( k 2 ) O(k^2) O(k2),如果 p > 1 p>1 p>1, k = p k=p k=p;如果 p < 1 p<1 p<1, k = 1 k=1 k=1。最终整个算法的时间复杂度为 O ( n + m k 2 ) O(n+mk^2) O(n+mk2),显然,当 m m m和 k k k的值变小时,时间复杂度会降低。
当数据空间出现一个或多个聚类,并且 p < 1 p<1 p<1, k = 1 k=1 k=1的情况,尽管 k k k足够小, E p s Eps Eps矩形区域的点数也会随着网格单元的增大而显著增加,很明显,这里的时间复杂度大于 p = 1 p=1 p=1时的复杂度。当 p ⩾ 1 p\geqslant 1 p⩾1时, k = p k=p k=p, E p s Eps Eps矩形区域减小,但随着 k k k的增大, k 2 k^2 k2明显增大。对于哪一种情况的产生的更显著取决于聚类的属性。
[参考文献]
[1] Meng’Ao L, Dongxue M, Songyuan G, et al. Research and improvement of DBSCAN cluster algorithm[C]. 2015 7th International Conference on Information Technology in Medicine and Education (ITME). IEEE, 2015: 537-540.