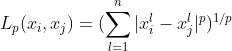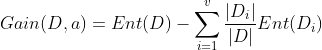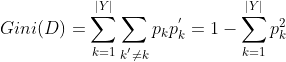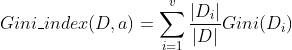机器学习-分类-k近邻与决策树

二、k近邻与决策树

1.k近邻

原理：

如果一个样本在特征空间中的k个最相似（特征空间中最邻近）的样本中的大多数属于某一个类别，则该样本也被分到这一类别。即某个样本的类别由与它最相近的k个样本投票得出。通俗的说就是少数服从多数。

有以下几点需要说明：

（1）k的选取

k过小意味着整体模型会变得复杂，容易发生过拟合；k过大会导致与输入实例较远的样本也会起到预测作用，使得预测错误的概率增加。通常采用交叉验证的方法来选取最优的k。

（2）距离的度量

常用的距离度量方法有曼哈顿距离、欧式距离等。

之间的L_p距离定义为：

当p=1时为曼哈顿距离；当p=2时为欧氏距离。

（3）特征归一化

在处理不同取值范围的特征值时，常采用的方法是将数值归一化，将每一个特征值的取值范围归一化到0~1或者-1~1。

常采用的归一化方法为极差归一化：

过程：

（1）给定样本点，计算数据集中所有点到该点的距离，按照距离进行排序。

（2）选取与样本点距离最小的k个点。

（3）确定这k个点所在类别出现的频率。

（4）返回这k个点所在类别出现频率最高的类别作为预测结果。

python代码：

from sklearn import datasets#导入数据集
from sklearn.preprocessing import MinMaxScaler#归一化
from sklearn.model_selection import train_test_split#划分数据集
from sklearn.metrics import accuracy_score#评分
from scipy.spatial import distance#计算距离
import numpy as np
import operator#排序

#计算欧氏距离
#设每个样本有m个属性，训练集一共有n个数据
#row就代表新输入的那个样本，因为只是一个数据，所以是1*m维的
#Matrix代表整个训练集，是个n*m维的。
#下面的函数用来计算新输入的样本与整个训练集的欧氏距离
def my_matEuclidean(row,Matrix):
    dataSetSize=Matrix.shape[0]#提取出训练集所含有的样本数。
    #np.tile(a,(y=c,x=d))是将a沿着y轴复制c次，沿着x轴复制d次的意思。
    #所以下面就是将这个1*m维的新样本沿着y轴复制n次，沿着x轴复制1次（其实就是不复制），使它也变为n*m维的矩阵，方便与Matrix做计算。
    diffMat=np.tile(row,(dataSetSize,1))-Matrix
    sqDiffMat=diffMat**2
    #axis=1表示对每一行求和，就是说沿着列的方向压缩。
    sqDistance=sqDiffMat.sum(axis=1)
    distance=sqDistance**0.5
    return distance

#knn算法
class MyKNN:
    def __init__(self,n_neighbors):
        self.n_neighbors=n_neighbors
        self.x_train=None
        self.y_train=None
    
    def fit(self,x_train,y_train):
        self.x_train=x_train
        self.y_train=y_train
        
    def __closest(self,row):
        #计算每一个测试数据与训练数据集中每一个数据的距离，并按照从小到大排序
        distance=my_matEuclidean(row, x_train)
        #argsort函数是先将数据集从小到大排序，再输出其索引。
        sortedDistance=distance.argsort()
        
        #获取前k个数据的标签并按照出现次数排序，返回出现次数最多的标签
        classCount={}
        for i in range(self.n_neighbors):
            voteLabel=y_train[sortedDistance[i]]
            #字典.get(key,default)表示返回字典中要查找的key对应的value,如果找不到key则返回default的值。
            #这是个计数函数，记录每一类（0，1，2）出现的次数。
            #如果在原来的字典中能找到某一类的标签，则在其次数上+1次即可
            #如果在原来字典中找不到这一类的标签，说明还没出现过，令其原始次数为0再+1次。
            classCount[voteLabel]=classCount.get(voteLabel,0)+1
        maxCount=0
        #循环找到有最多次数的类
        for key,value in classCount.items():
            if value>maxCount:
                maxCount=value
                classes=key
        return classes
    
    def predict(self,x_test):
        predicts=[]
        for row in x_test:
            label=self.__closest(row)
            predicts.append(label)
        return predicts
    
    


#调用
iris=datasets.load_iris()
x=iris.data
y=iris.target
#划分数据集
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.3)
#归一化
minMax=MinMaxScaler()
x_train=minMax.fit_transform(x_train)
x_test=minMax.fit_transform(x_test)
#测试
best_score=0.0
best_k=0
for k in range(30,1,-1):#从30开始调试k
    my_classification=MyKNN(k)
    my_classification.fit(x_train,y_train)
    predicts=my_classification.predict(x_test)
    score=accuracy_score(y_test,predicts)
    if score>best_score:
        best_score=score
        best_k=k
        

2.决策树

原理：

样本所有特征中有一些特征在分类时起到决定性作用，决策树的构造过程就是找到这些具有决定性作用的特征，根据其决定性作用的大小来逐层构造决策树。本质上是根据数据特征将数据集逐层分类的过程。

过程：

（1）特征选择：从训练集数据的众多特征中选择一个最优特征作为当前节点的分裂标准。不同的特征选择准则有信息增益、信息增益率和基尼指数。

①信息增益

ID3算法是利用信息增益作为选取特征准则。

信息增益是信息熵（不确定信息）的下降。

信息熵用来度量样本集合纯度。假设当前样本集合D中第k类样本所占的比例为（k=1,2,3,...|Y|），则数据集D的信息熵定义为：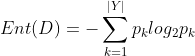

信息熵越小意味着数据集纯度越高。

假设离散属性a具有v个可能取值，若使用属性a对数据集进行划分，则会产生v个分支节点，其中第i个分支节点包含了D中所有在属性a上取值为的数据，记为 。考虑到每一类中包含的样本数据量的不同，赋予每一个节点权重为，即该节点样本量占所有样本量的比例。

则利用属性a对数据集进行划分的信息增益为：

一般而言，信息增益越大，意味着利用属性a对数据集进行划分所获得的纯度提升越大。

②信息增益率

C4.5算法以信息增益率作为选取特征准则

信息增益率改善了信息增益可能对取值较多的属性有所偏好的缺点。

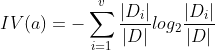称为属性a的固有值，一般来说属性a的去取值越多，固有值越大。

但是信息增益率准则可能对取值较少的属性有所偏好。

所以C4.5算法并不是直接选取信息增益率最大的属性，而是先选出信息增益高于平均水平的属性，再从这些属性中选取信息增益率最高的属性。

③基尼指数

CART算法使用基尼指数作为选取特征准则。

基尼值定义为：

基尼值反映了从数据集中随机抽取两个样本，其类别标签不一致的概率。因此基尼值越小，纯度越高。

基尼指数的定义为：

在属性集A中，选择那个使得划分后基尼指数最小的属性特征。

在选取了划分数据集的特征后，要在该特征的特征值中选取一个作为划分标准。选取的准则同样按照信息增益、信息增益率、基尼指数进行。

（2）决策树生成：根据选择的特征评估标准，从上至下递归地生成子节点，直到数据集不可分。

python代码：

#导入库
import numpy as np
from sklearn import tree #决策树构建
from sklearn.datasets import load_iris
from sklearn.model_selection import GridSearchCV #查找最优参数
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

#加载数据集
data=load_iris()
feature_names=data.get('feature_names')#属性名称
target_names=data.get('target_names')#标签名称
x=data.get('data')#数据集
y=data.get('target')#标签集
#划分训练集和测试集
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.3)

#设置参数矩阵并找到最优参数
#np.linspace(a,b,c)函数用来返回(a,b)间等间隔的数组，元素的个数为c.
#np.linspace(0,1,100)将(0,1)等分为100份，返回其分点。
entropy_thresholds=np.linspace(0,1,100)
gini_thresholds=np.linspace(0,0.2,100)
param_grid=[{'criterion':['entropy'],'min_impurity_decrease':entropy_thresholds},{'criterion':['gini'],'min_impurity_decrease':gini_thresholds},{'max_depth':np.arange(1,4)},{'min_samples_split':np.arange(2,30,1)}]
#GridSearchCV，它存在的意义就是自动调参，只要把参数输进去，就能给出最优化结果和参数。但是这个方法适合于小数据集，一旦数据的量级上去了，很难得到结果。
#它将网格调参与交叉验证相结合。
#GridSearchCV(estimator,param_grid,cv),estimator为分类器，cv为表示进行k折交叉验证（把数据集分为k份，每次取一份作为测试集）
clf=GridSearchCV(tree.DecisionTreeClassifier(),param_grid,cv=5)
clf.fit(x,y)
print("best param:{0}\nbest score:{1}".format(clf.best_params_,clf.best_score_))

#利用最优参数构建决策树
#决策树有三个参数：criterion='gini'或者'entropy';max_depth为树的最大深度；min_samples_split：拆分内部节点所需要的最小样本数。
clf=tree.DecisionTreeClassifier(criterion='gini',max_depth=3)
clf.fit(x_train,y_train)

predicts=clf.predict(x_test)
accuracy=accuracy_score(y_test,predicts)

#画出决策树并保存
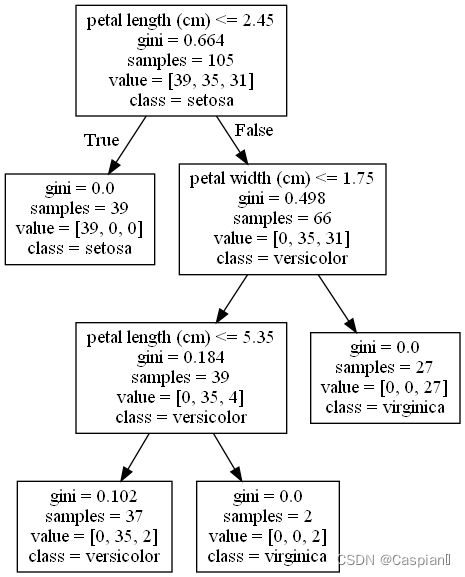
with open("tree.dot","w") as f:
    f=tree.export_graphviz(clf,feature_names=feature_names,class_names=target_names,out_file=f)

之后我们得到了一个dot文件，可以通过Graphviz将其转化为决策树形式，具体方法如下：

http://www.graphviz.org/download/官网下载适合自己的版本

打开电脑的cmd，将路径转到存放着tree.dot的文件夹下

运行语句dot -Tpng tree.dot -o tree.png

dot表示使用的是dot布局，其他布局相应的修改即可，-T表示格式，即画成png格式，-o表示重命名为tree.png。

就可以在当前目录下得到以png格式存储的决策树了: