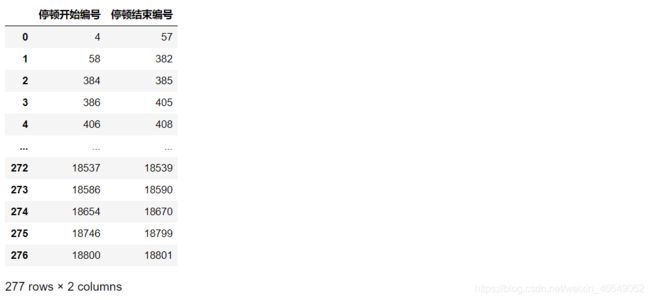数据挖掘实战—家用热水器用户行为分析与事件识别

---

案例数据百度网盘链接-提取码：1234
传送门：

• 数据挖掘实战—财政收入影响因素分析及预测
• 数据挖掘实战—航空公司客户价值分析
• 数据挖掘实战—商品零售购物篮分析
• 数据挖掘实战—基于水色图像的水质评价
• 数据挖掘实战—家用热水器用户行为分析与事件识别
• 数据挖掘实战—电商产品评论数据情感分析

---

引言

  居民在使用家用热水器的过程中，会因为地区气候、不同区域和用户年龄性别差异等原因形成不同的使用习惯。家电企业若能深入了解其产品在不同用户群中的使用习惯，从而产商便可以对不同的客户群提供最适合的个性化产品，制定相应的营销策略，开拓新市场。定义挖掘目标如下：

1. 根据热水器采集到的数据，划分一次完整的用水事件
2. 在划分好的一次完整用水事件中，识别出洗浴事件

数据挖掘步骤：

1. 对热水器用户的历史用水数据进行选择性抽取，构建专家样本
2. 数据探索分析与预处理，包括探索水流量的分布情况，删除冗余属性，识别用水数据的缺失值，并对缺失值进行处理，然后根据建模的需要进行属性构造等。最后根据以上处理，对热水器用户用水样本数据建立用水事件时间间隔识别模型和划分一次完整的用水事件模型，接着在一次完整用水事件划分结果的基础上，剔除短暂用水事件、缩小识别范围等。
3. 在步骤2得到的建模样本数据基础上，建立洗浴事件识别模型，对洗浴事件识别模型进行模型分析评价
4. 应用步骤3形成的模型结果，并对洗浴事件划分进行优化
5. 调用洗浴事件识别模型，对实时监控的热水器流水数据进行洗浴事件自动识别。

一、数据探索分析

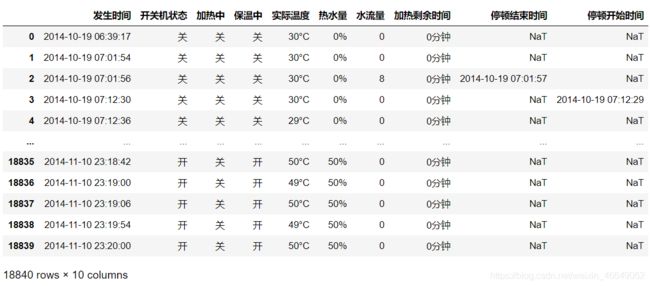
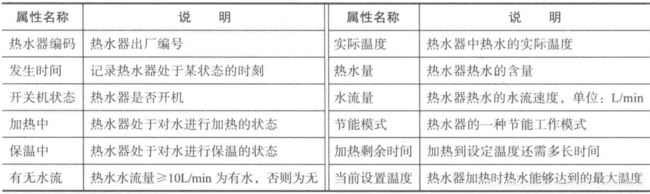
  热水器采集的用水数据包含12个属性:热水器编码、发生时间、开关机状态、加热中、保温中、有无水流、实际温度、热水量、水流量、节能模式、加热剩余时间和当前设置温度等。其解释说明如下：

1.数据质量分析

1.1缺失值分析

data.isnull().sum()

发现没有缺失值

1.2 异常值分析

for column in data.columns:
    print(data[column].value_counts())

通过对每一列的值进行统计，发现没有异常值。并且发现热水器编号、节能模式、当前设置温度均为常量

1.3 重复数据分析

data.duplicated().sum()

发现没有重复数据

2.数据特征分析

2.1 分布分析

  探索热水器的水流量情况，其中“有无水流”和“水流量”可以直观的显示水量情况
  查看有无水流的分布

lv_none = data['有无水流'].value_counts()['无']
lv_move = data['有无水流'].value_counts()['有']
# 直方图展示有无水流列中的情况
plt.rcParams['font.sans-serif'] = [u'simHei']
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(8,8))
# plt.hist(data['有无水流'],bins='auto',color='skyblue')
# 绘制柱状图
plt.bar(x = ['无','有'],height=[lv_none,lv_move],width=0.4,alpha=0.8,color='skyblue')
plt.xlabel('水流状态',fontsize=15)
plt.ylabel('记录数',fontsize=15)
plt.title('不同水流状态记录数',fontsize=20)

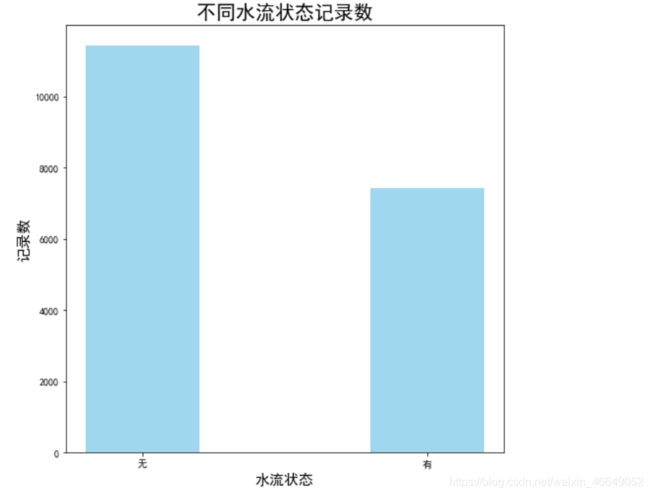
从图中可以看出无水流状态比有水流状态要多
  查看水流量分布的箱型图

fig,ax = plt.subplots(figsize=(8,8))
sns.boxplot(data['水流量'],orient='v')
ax.set_xlabel('水流量',fontsize=15)
ax.set_title('水流量分布箱型图',fontsize=20)
plt.grid(axis='y')  # 网格线

从箱型中可以看出：箱体贴近于0，无水流量或者水流量小的时候多，与水流状态的分布一致

三、数据预处理

1.数据归约之属性归约

  在前面，我们已经知道热水器编号、节能模式、当前设置温度均为常量，并且水流状态可以根据“水流量”属性来表现出来。因此，将这四个冗余属性热水器编号、节能模式、当前设置温度、有无水流删除。

# 删除冗余属性
data.drop(labels=['热水器编号','有无水流','节能模式','当前设置温度'],axis=1,inplace=True)
data.to_csv('water_heart.csv',index=False)

2.数据归约之数值归约

  热水器用户的用水数据存储在数据库中，记录了各种各样的用水事件，包括洗浴、洗手、刷牙、洗脸、洗衣、洗菜等，而且一次用水事件由数条甚至数千条的状态记录组成。所以首先需要在大量的状态记录中划分出哪些连续的数据是一次完整的用水事件。在用水状态记录中，水流量不为0，表明热水器用户正在使用热水;而水流量为0时，则表明热水器用户用热水时发生停顿或者用热水结束。对于任何一个用水记录，如果它的向前时差超过阈值T，则将它记为事件的开始编号;如果它的向后时差超过阈值T，则将其记为事件的结束编号。
一次完整用水事件的划分步骤：

1. 读取数据记录，识别所有水流量不为0的状态记录，将它们的发生时间记为序列t1
2. 对序列t1构建其向前时差列和向后时差列，并分别与阈值进行比较。向前时差超过阈值T，则将它记为新的用水事件的开始编号;如果向后时差超过阈值T，则将其记为用水事件的结束编号。
3. 循环执行步骤2，直至向前时差列与向后时差列和均值比较完毕，则结束事件划分。

第一步：确定单次用水事件时长阈值

# 确定单词用水事件时长阈值
n = 4  # 使用以后四个点的平均斜率
threshold = pd.Timedelta(minutes=5)  # 专家阈值
data['发生时间'] = pd.to_datetime(data['发生时间'], format='%Y%m%d%H%M%S')
data = data[data['水流量'] > 0]  # 只要流量大于0的记录
# 自定义函数：输入划分时间的时间阈值，得到划分的事件数
def event_num(ts):
    d = data['发生时间'].diff() > ts  # 相邻时间作差分，比较是否大于阈值
    return d.sum() + 1  # 这样直接返回事件数
dt = [pd.Timedelta(minutes=i) for i in np.arange(1, 9, 0.25)]
h = pd.DataFrame(dt, columns=['阈值'])  # 转换数据框，定义阈值列
h['事件数'] = h['阈值'].apply(event_num)  # 计算每个阈值对应的事件数
h['斜率'] = h['事件数'].diff()/0.25  # 计算每两个相邻点对应的斜率
h['斜率指标']= h['斜率'].abs().rolling(4).mean()  # 往前取n个斜率绝对值平均作为斜率指标
# 用idxmin返回最小值的Index，由于rolling_mean()计算的是前n个斜率的绝对值平均,所以结果要进行平移（-n）
ts = h['阈值'][h['斜率指标'].idxmin() - n]
if ts > threshold:
    ts = pd.Timedelta(minutes=4)
print('计算出的单次用水时长的阈值为：',ts)

1. 当存在一个阈值的斜率指标K<1时，则取阈值最小的点A(可能存在多个阈值的斜率指标小于1)的横坐标x作为用水事件划分的阈值，具中K<1中的“1”是经过实际数据验证的一个专家阈值。
2. 当不存在一个阈值的斜率指标K<1时，则找所有阈值中斜率指标最小的阈值;如果该阈值的斜率指标小于5，则取该阈值作为用水事件划分的阈值;如果该阈值的斜率指标不小于5，则阈值取默认值的阈值——4分钟。其中，斜率指标小于“5”中的“5"是经过实际数据验证的一个专家阈值。

其中斜率指标指的是某段阈值范围内的趋势变化。如果斜率指标比较大，那么说明某段阈值范围内，下降趋势明显，说明在该段阈值范围内，热水器用户的停顿习惯比较集中。如果趋势比较平缓，则说明热水器用户停顿热水的习惯趋于稳定，所以取该段时间开始的时间点作为阈值，既不会将短的用水事件合并，又不会将长的用水事件拆开。

第二步：利用得到的时长阈值划分用水事件

# 设置阈值T
threshold = pd.Timedelta('4 min')
# 将时间转变成时间索引格式
data['发生时间'] = pd.to_datetime(data['发生时间'],format='%Y%m%d%H%M%S')
# 选取所有水流量不为0的数据
data = data[data['水流量'] != 0]

# 构建向前时差列
sjks = data['发生时间'].diff() > threshold
# 令第一个时间为第一个用水事件的开始事件
sjks.iloc[0] = True 
# 构建向后时差列
sjJs = sjks.iloc[1:]
# 令最后一个时间作为最后一个用水事件的结束时间
sjJs = pd.concat([sjJs,pd.Series(True)])
# 创建数据框，定义用水事件序列
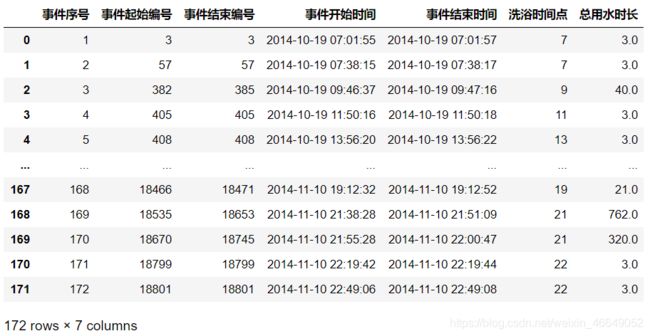
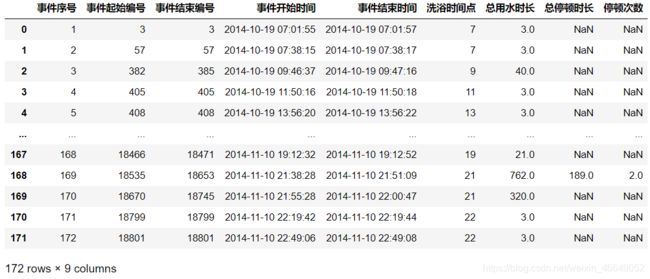
sj = pd.DataFrame(np.arange(1,sum(sjks)+1),columns=['事件序号'])
sj['事件起始编号'] = data.index[sjks == 1] + 1  # 定义用水事件起始编号
sj['事件结束编号'] = data.index[sjJs == 1] + 1   # 定义用水事件结束编号
sj.to_csv('sj.csv',index=False)

3. 数据集成之属性构造

3.1 构造用水时长与频率属性

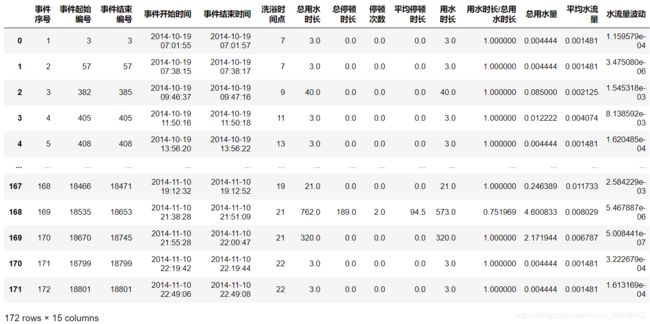
  不同用水事件的用水时长是基础属性之一。例如，单次洗漱事件一般总时长在5分钟左右，而一次手洗衣物事件的时长则根据衣物多少而不同。根据用水时长这一属性可以构建如表所示的事件开始时间、事件结束时间、洗浴时间点、用水时长、总用水时长和用水时长/总用水时长这6个属性。

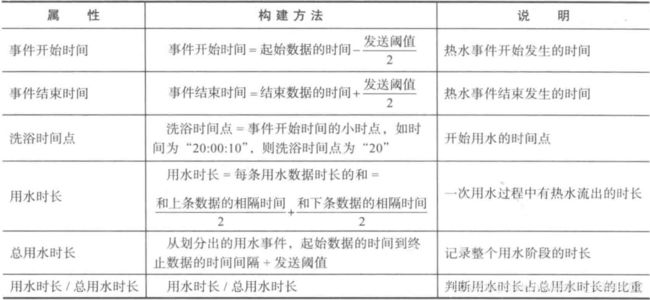
其中，用水开始时间或结束时间两个特征时分别减去或加上了发送阈值（发送阈值是指热水器传输数据的频率的大小)。在20:00:10时，热水器记录到的数据是数据还没有用水，而在20:00:12时，热水器记录的数据是有用水行为。所以用水开始时间在20:00:10~20:00:12之间，考虑到网络不稳定导致的网络数据传输延时数分钟或数小时之久等因素，取平均值会导致很大的偏差，综合分析构建“用水开始时间”为起始数据的时间减去“发送阈值”的一半。
  用水时长相关的属性只能区分出一部分用水事件，不同用水事件的用水停顿和频率也不同。例如，一次完整洗漱事件的停顿次数不多，停顿的时间长短不一，平均停顿时长较短;一次手洗衣物事件的停顿次数较多，停顿时间相差不大，平均停顿时长一般。根据这一属性，可以构建如表所示的停顿时长、总停顿时长、平均停顿时长、停顿次数4个属性。

# 读取热水器使用记录
data = pd.read_csv('water_heart.csv',header=0)
# 读取用水事件记录
sj = pd.read_csv('sj.csv',header=0)

# 转换时间格式
data['发生时间'] = pd.to_datetime(data['发生时间'],format='%Y%m%d%H%M%S')
timeDel = pd.Timedelta('1 sec')  # 发送阈值的一半
# 构造属性-事件开始时间
sj['事件开始时间'] = data.iloc[sj['事件起始编号']-1,0].values- timeDel   # 使用values是因为索引不同
# 构造属性-事件结束时间
sj['事件结束时间'] = data.iloc[sj['事件结束编号']-1,0].values + timeDel
# 构造属性-洗浴时间点
sj['洗浴时间点'] = [i.hour for i in sj['事件开始时间']]
# 构造属性-总用水时长
sj['总用水时长'] = np.int64(sj['事件结束时间'] - sj['事件开始时间'])/1000000000 + 1

# 构造用水停顿事件
# 构造属性-用水停顿开始时间，用水停顿结束时间
for i in range(len(data) - 1):
    # 停顿开始指的是从有水流到无水流
    if data.loc[i,'水流量'] != 0 and data.loc[i+1,'水流量'] == 0:
        data.loc[i+1,'停顿开始时间'] = data.loc[i+1,'发生时间'] - timeDel
    # 停顿结束指的是从无水流到有水流
    if data.loc[i,'水流量'] == 0 and data.loc[i+1,'水流量'] != 0:
        data.loc[i+1,'停顿结束时间'] = data.loc[i+1,'发生时间'] + timeDel

# 提取停顿开始时间与停顿结束时间的行号
indStopStart = data.index[data['停顿开始时间'].notnull()] + 1
indStopEnd = data.index[data['停顿结束时间'].notnull()] + 1
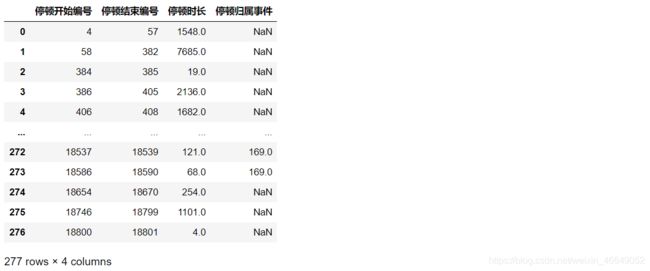
Stop = pd.DataFrame(data = {'停顿开始编号':indStopStart[:-1],
                           '停顿结束编号':indStopEnd[1:]})

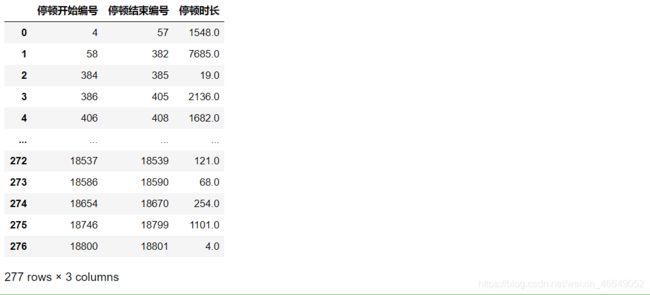
# 构建属性-停顿时长
Stop['停顿时长'] = np.int64(data.loc[indStopEnd[1:]-1,'停顿结束时间'].values - data.loc[indStopStart[:-1] - 1,'停顿开始时间'].values)/ 1000000000

# 将每次停顿与事件匹配，停顿开始的时间要大于事件开始的时间,停顿结束时间要小于事件结束时间
for i in range(len(sj)):
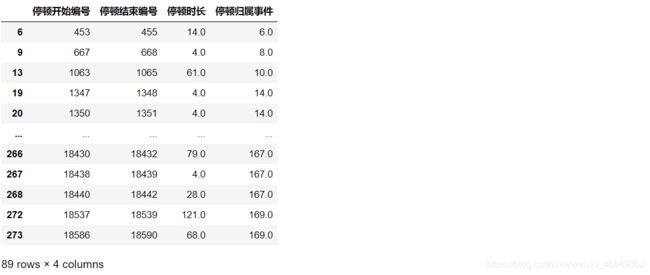
    Stop.loc[(Stop['停顿开始编号'] > sj.loc[i,'事件起始编号']) & (Stop['停顿结束编号'] < sj.loc[i,'事件结束编号']),'停顿归属事件'] = i+1

# 删除停顿次数为0的事件
Stop = Stop[Stop['停顿归属事件'].notnull()]

# 构造属性-用水事件停顿总时长、停顿次数、停顿平均时长
stopAgg = Stop.groupby(['停顿归属事件']).agg({'停顿时长':sum,'停顿开始编号':len},axis=0)

sj.loc[stopAgg.index-1,'总停顿时长'] = stopAgg.loc[:,'停顿时长'].values
sj.loc[stopAgg.index-1,'停顿次数'] = stopAgg.loc[:,'停顿开始编号'].values

# 对缺失值进行处理
sj.fillna(0,inplace=True)
# 对存在停顿的事件构造平均停顿时长
stopNo0 = sj['停顿次数'] != 0
sj.loc[stopNo0,'平均停顿时长'] = sj.loc[stopNo0,'总停顿时长'] / sj.loc[stopNo0,'停顿次数']

# 对缺失值进行处理
sj.fillna(0,inplace=True)
# 构造属性-用水时长=总用水时长-总停顿时长
sj['用水时长'] = sj['总用水时长'] - sj['总停顿时长']
# 构造属性-用水时长/总用水时长
sj['用水时长/总用水时长'] = sj['用水时长'] / sj['总用水时长']

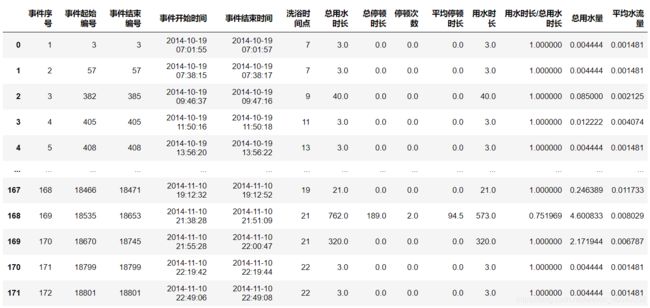
此时，用水事件表中的属性有[‘事件序号’, ‘事件起始编号’, ‘事件结束编号’, ‘事件开始时间’, ‘事件结束时间’, ‘洗浴时间点’, ‘总用水时长’,‘总停顿时长’, ‘停顿次数’, ‘平均停顿时长’, ‘用水时长’, ‘用水时长/总用水时长’]。

3.2 构建用水量与波动属性

  除了用水时长、停顿和频率外，用水量也是识别该事件是否为洗浴事件的重要属性。例如，用水事件中的洗漱事件相比洗浴事件有停顿次数多、用水总量少、平均用水少的特点;手洗衣物事件相比于洗浴事件则有停顿次数多、用水总量多、平均用水量多的特点。根据这一原因可以构建出两个用水量属性。

  同时用水波动也是区分不同用水事件的关键。一般来说，在一次洗漱事件中，刷牙和洗脸的用水量完全不同;而在一次手洗衣物事件中，每次用水的量和停顿时间相差却不大。根据不同用水事件的这一特征可以构建水流量波动和停顿时长波动两个特征。

  在用水时长和频率属性的基础之上构建用水量和用水波动属性，需要充分利用用水时长与频率属性。

# 构造属性-总用水量
# L/min ==> L/s
data['水流量']  = data['水流量'] / 60
# 初始值赋为0
sj['总用水量'] = 0
for i in range(len(sj)):
    start = sj.loc[i,'事件起始编号'] - 1
    end = sj.loc[i,'事件结束编号'] - 1
    if start != end:
        for j in range(start,end):
            if data.loc[j,'水流量'] != 0:
                sj.loc[i,'总用水量'] = (data.loc[j+1,'发生时间'] - data.loc[j,'发生时间']).seconds * data.loc[j,'水流量'] + sj.loc[i,'总用水量']
            # 加上结束时刻的水流量
        sj.loc[i,'总用水量'] += data.loc[end,'水流量'] * 2
    else:
        sj.loc[i,'总用水量'] += data.loc[start,'水流量'] * 2

# 构造属性-平均水流量
sj['平均水流量'] = sj['总用水量'] / sj['用水时长']

# 构造属性-水流量波动
# 给予一个初值
sj['水流量波动'] = 0
for i in range(len(sj)):
    start = sj.loc[i,'事件起始编号'] - 1
    end = sj.loc[i,'事件结束编号'] - 1
    for j in range(start,end+1):
        if data.loc[j,'水流量'] != 0:
            slbd = (data.loc[j,'水流量'] - sj.loc[i,'平均水流量']) ** 2
            slsj = (data.loc[j+1,'发生时间'] - data.loc[j,'发生时间']).seconds
            sj.loc[i,'水流量波动'] += (slbd * slsj)
    sj.loc[i,'水流量波动'] = sj.loc[i,'水流量波动'] / sj.loc[i,'用水时长']

# 构建属性-停顿时长波动
# 给予一个初值0
sj['停顿时长波动'] = 0
for i in range(len(sj)):
    # 当停顿次数为0或1时，停顿时长波动为0
    if sj.loc[i,'停顿次数'] > 0:
        for j in Stop.loc[Stop['停顿归属事件'] == (i+1),'停顿时长'].values:
            sj.loc[i,'停顿时长波动'] = ((j - sj.loc[i,'平均停顿时长']) ** 2) * j + sj.loc[i,'停顿时长波动']
        sj.loc[i,'停顿时长波动'] = sj.loc[i,'停顿时长波动'] / sj.loc[i,'总停顿时长']

此时，用水事件表中的属性有[‘事件序号’, ‘事件起始编号’, ‘事件结束编号’, ‘事件开始时间’, ‘事件结束时间’, ‘洗浴时间点’, ‘总用水时长’, ‘总停顿时长’, ‘停顿次数’, ‘平均停顿时长’, ‘用水时长’, ‘用水时长/总用水时长’, ‘总用水量’, ‘平均水流量’, ‘水流量波动’, ‘停顿时长波动’]。

4.筛选候选洗浴事件

  由于我们建立的是洗浴事件识别模型，所以在一次完整用水事件划分结果的基础上，剔除短暂用水事件。可以使用3个比较宽松的条件筛选掉那些非常短暂的用水事件，确定不可能为洗浴事件的数据就删除，剩余的事件称为“候选洗浴事件”。这3个条件是“或”的关系。

1. 一次用水事件中总用水量小于5升
2. 用水时长小于100秒
3. 总用水时长小于120秒。

# 筛选条件
sj_bool = ((sj['用水时长']>100) & (sj['总用水时长'] > 120) & (sj['总用水量'] > 5))
sj_final = sj.loc[sj_bool,:]

筛选前，用水事件数目总共为172个，经过筛选，余下77个用水事件。

# 保存数据
sj_final.to_excel('sj_final.xlsx',index=False)

四、模型构建

from sklearn.preprocessing import StandardScaler
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers,optimizers,losses,metrics,Model
from tensorflow.keras.layers import Input, Dense, BatchNormalization,Lambda
from sklearn.metrics import classification_report,accuracy_score,roc_curve #分类报告

# 构造训练集与测试集
# 通过事件序号，将label与sj_final进行拼接
data_tr = pd.merge(sj_final,pd.DataFrame(label[['事件序号','标签']]),on=['事件序号'],how='inner')
x_train ,y_train= data_tr.iloc[:,5:-1],data_tr.iloc[:,-1]
data_te = pd.read_excel('data/test_data.xlsx')
x_test,y_test = data_te.iloc[:,4:-1],data_te.iloc[:,-1]

# 标准化
sts = StandardScaler()
x_scale = sts.fit(x_train)
x_train = x_scale.transform(x_train)
x_test = x_scale.transform(x_test)

# 建立BP模型
def MLP(input_dim,output_dim,hidden_layers):
    inputs = Input(shape=(input_dim,))
    x = BatchNormalization()(inputs)
    for i in hidden_layers:
        x = Dense(i)(x)
        x = BatchNormalization()(x)
        x = Lambda(tf.keras.activations.relu)(x)
    output = Dense(1,activation='sigmoid')(x)
    model = Model(inputs=inputs,outputs=output)
    # 模型编译
    model.compile(optimizer=optimizers.Adam(learning_rate=0.001),
                 loss= losses.BinaryCrossentropy(from_logits=True,label_smoothing=0.0005),
                 metrics=['accuracy'])
    return model
hid = [17,10]
mlp = MLP(11,1,hid)

history = mlp.fit(x_train,y_train,batch_size=15,epochs=200)
# 加载模型
y_pred = mlp.predict(x_test)
y_pred[y_pred >= 0.5] = 1
y_pred[y_pred < 0.5] = 0
print(y_pred)
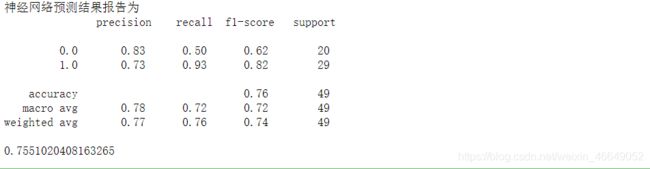
print('神经网络预测结果报告为\n',classification_report(y_pred,y_test))
print(accuracy_score(y_pred,y_test))

plt.rcParams['font.sans-serif'] = 'SimHei'  # 显示中文
plt.rcParams['axes.unicode_minus'] = False  # 显示负号
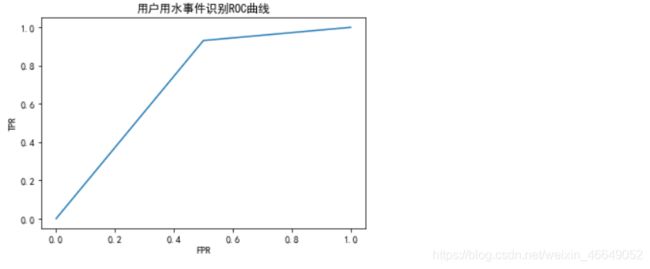
fpr, tpr, thresholds = roc_curve(y_pred,y_test)  # 求出TPR和FPR
plt.figure(figsize=(6,4))  # 创建画布
plt.plot(fpr,tpr)  # 绘制曲线
plt.title('用户用水事件识别ROC曲线')  # 标题
plt.xlabel('FPR')  # x轴标签
plt.ylabel('TPR')  # y轴标签
plt.savefig('用户用水事件识别ROC曲线.png')  # 保存图片
plt.show()  # 显示图形

模型效果勉勉强强

参考于《python数据分析与挖掘实战》

---

如果对您有帮助，麻烦点赞关注，这真的对我很重要！！！如果需要互关，请评论或者私信！

---