循环神经网络前言知识-序列模型

笔记来源视频：跟李沐学AI的个人空间_哔哩哔哩_bilibili

序列数据

在实际生活中，很多数据都是有时序结构的

电影的评价随时间变化而变化

• 获奖之后评分上升，直到奖项被忘记
• 看了很多同款题材的好电影之后，人们的期望变高
• 季节性：贺岁片，暑期档
• 导演、演员的负面报道导致评分变低

更多例子：

• 音乐、语言、文本和视频都是连续的
•         标题“狗咬人”远没有“人咬狗”那么惊讶
• 预测明天的股价要比填补昨天遗失的股价更困难

统计工具

 

给定前面t-1个数据，然后预测第t个数据，对前面t-1个数据进行建模，这样的模型叫做自回归模型。

 建模方案

方案A-马尔科夫假设

假设当前数据只跟过去T个数据点相关（T是一个定量，不会随着时间的变化而改变）

T=2的情况

 只对过去T个数据进行建模

 MLP(Multi-layer Perceptron):多层感知器,是一个前馈式的、具有监督的人工神经网络结构。通过多层感知器可包含多个隐藏层,实现对非线性数据的分类建模。

 方案B-潜变量模型

 将过去的信息将函数的形式转化为变量的形式

这样的话h就是不断更新的，随着时间的推移，过去的数据会发生更新。

 总结：

• 时序模型中，当前数据跟之前观察到的数据相关
• 自回归模型使用自身过去数据来预测未来
• 马尔科夫模型假设当前只跟最近少数数据相关，从而简化模型
• 潜变量模型使用潜变量来概括历史信息

代码实现

下载d2l包的链接：

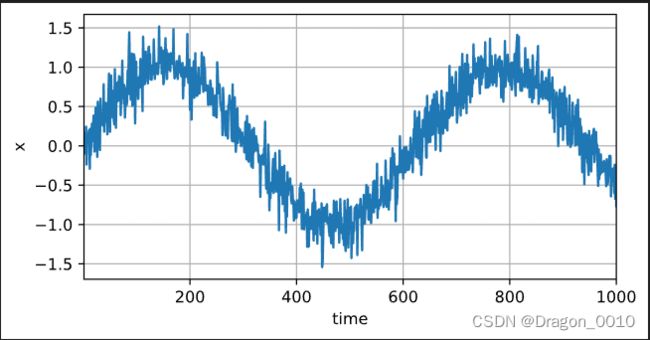
pip install -i https://pypi.douban.com/simple/ d2l

#首先，我们生成一些数据：使用正弦函数和一些可加性噪声来生成序列数据， 
#时间步为1,2...1000
%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2l

T = 1000  # 总共产生1000个点
time = torch.arange(1, T + 1, dtype=torch.float32)
x = torch.sin(0.01 * time) + torch.normal(0, 0.2, (T,))
d2l.plot(time, [x], 'time', 'x', xlim=[1, 1000], figsize=(6, 3))

tau = 4
features = torch.zeros((T - tau, tau))
for i in range(tau):
    features[:, i] = x[i: T - tau + i]
labels = x[tau:].reshape((-1, 1))

batch_size, n_train = 16, 600
# 只有前n_train个样本用于训练
train_iter = d2l.load_array((features[:n_train], labels[:n_train]),
                            batch_size, is_train=True)

# 初始化网络权重的函数
def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.xavier_uniform_(m.weight)

# 一个简单的多层感知机
def get_net():
    net = nn.Sequential(nn.Linear(4, 10),
                        nn.ReLU(),
                        nn.Linear(10, 1))
    net.apply(init_weights)
    return net

# 平方损失。注意：MSELoss计算平方误差时不带系数1/2
loss = nn.MSELoss(reduction='none')

def train(net, train_iter, loss, epochs, lr):
    trainer = torch.optim.Adam(net.parameters(), lr)
    for epoch in range(epochs):
        for X, y in train_iter:
            trainer.zero_grad()
            l = loss(net(X), y)
            l.sum().backward()
            trainer.step()
        print(f'epoch {epoch + 1}, '
              f'loss: {d2l.evaluate_loss(net, train_iter, loss):f}')

net = get_net()
train(net, train_iter, loss, 5, 0.01)

 预测部分

onestep_preds = net(features)
d2l.plot([time, time[tau:]],
         [x.detach().numpy(), onestep_preds.detach().numpy()], 'time',
         'x', legend=['data', '1-step preds'], xlim=[1, 1000],
         figsize=(6, 3))