《Deeplearning with python》读书笔记-第一部分 二分类、多分类、回归问题样例

二分类、多分类、回归问题样例

 

二分类问题（电影评论划分为正面或者负面）

多分类问题（将新闻按主题分类）

回归问题（根据房地产数据估算房屋价格）

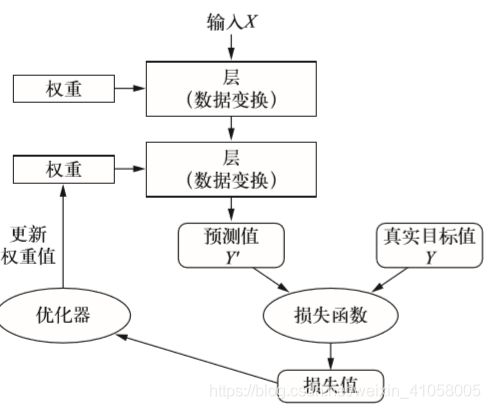
多个层链接在一起组成了网络，将输入数据映射为预测值。然后损失函数将这些预测值与目标进行比较，得到损失值，用于衡量网络预测值与预期结果的匹配程度。优化器使用这个损失值来更新网络的权重。

         不同的张量格式与不同的数据处理类型需要用到不同的层。例如，简单的向量数据保存在形状为 (samples, features) 的 2D 张量中，通常用密集连接层［densely connected layer，也叫全连接层（fully connected layer）或密集层（dense layer），对应于Keras 的 Dense 类］来处理。序列数据保存在形状为 (samples, timesteps, features) 的 3D 张量中，通常用循环 层（recurrent layer，比如Keras 的 LSTM 层）来处理。图像数据保存在4D 张量中，通常用二维卷积层（Keras 的 Conv2D）来处理。层兼容性（layer compatibility）具体指的是每一层只接受特定形状的输入张量，并返回特定形状的输出张量。

输入是第一个维度大小为784的2D张量（第0 轴是批量维度，其大 小没有指定，因此可以任意取值）作为输入。使用Keras 时，你无须担心兼容性，因为向模型中添加的层都会自动匹配输入层的形状，例如下面这段代码。

其中第二层没有输入形状（input_shape）的参数，相反，它可以自动推导出输入形状等 于上一层的输出形状。

模型：层构成的网格。常见的网络拓扑结构如下：双分支（two-branch）网络，多头（multihead）网络，inception模块。

对于二分类问题，你可以使用二元交叉熵（binary crossentropy）损失函数；对于多分类问题，可以用分类交叉熵（categorical crossentropy）损失函数；对于回归问题，可以用均方误差（mean-squared error）损失函数；对于序列学习问题，可以用联结主义时序分类（CTC，connectionist temporal classification）损失函数。

Keras

相同的代码可以在 CPU 或 GPU 上无缝切换运行。

  具有用户友好的 API，便于快速开发深度学习模型的原型。

  内置支持卷积网络（用于计算机视觉）、循环网络（用于序列处理）以及二者的任意组合。

支持任意网络架构：多输入或多输出模型、层共享、模型共享等。这也就是说，Keras能够构建任意深度学习模型，无论是生成式对抗网络还是神经图灵机。

Keras 是一个模型级（model-level）的库，为开发深度学习模型提供了高层次的构建模块。 它不处理张量操作、求微分等低层次的运算。相反，它依赖于一个专门的、高度优化的张量库来完成这些运算，这个张量库就是Keras 的后端引擎（backend engine）。 Keras 没有选择单个张量库并将Keras 实现与这个库绑定，而是以模块化的方式处理这个问题（见图3-3）。因此，几个不同的后端引擎都可以无缝嵌入到 Keras 中。目前，Keras 有三个后端实现：TensorFlow后端、 Theano 后端和微软认知工具包（CNTK，Microsoft cognitive toolkit）后端。

推荐使用TensorFlow 后端作为大部分深度学习任务的默认后端，因为它的应用最广泛，可扩展，而且可用于生产环境。在 CPU 上运行时，TensorFlow 本身封装了一个低层次的张量运算库，叫作Eigen；在GPU 上运行时，TensorFlow封装了一个高度优化的深度学习运算库，叫作 NVIDIA CUDA 深度神经网络库（cuDNN）。

定义模型有两种方法：一种是使用 Sequential 类（仅用于层的线性堆叠，这是目前最常 见的网络架构），另一种是函数式 API（functional API，用于层组成的有向无环图，让你可以构建任意形式的架构）。

 

二分类问题：电影评论分类

IMDB数据集

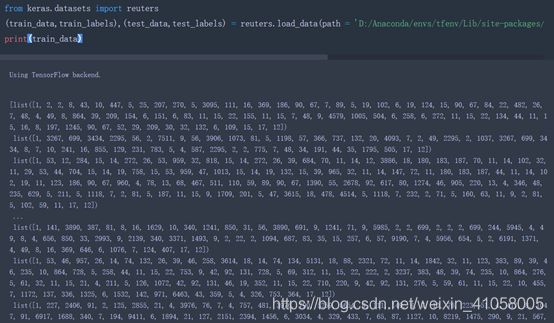
通过非常艰难的方法将数据集自己下载之后放在了路径中D:/Anaconda/envs/tfenv/Lib/site-packages/tensorflow_core/python/keras/api/keras/datasets/

也实现了功能，解码前的traindata和解码后的如下：

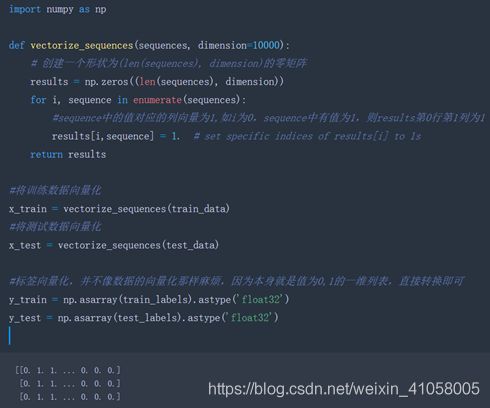
Imdb.npk是一个整数序列，要将它变成张量。方法一：填充列表，使其具有相同的长度（这是因为评论的长度是肯定不同的），再将列表转换成形状为 (samples, word_indices) 的整数张量，然后网络第一层使用能处理这种整数张量的层（即 Embedding 层）

方法二：对列表进行 one-hot 编码，将其转换为 0 和 1 组成的向量。举个例子，序列 [3, 5] 将会被转换为10 000 维向量，只有索引为3 和 5 的元素是1，其余元素都是0。然后网络第 一层可以用 Dense 层，它能够处理浮点数向量数据。

这里采取了第二种方法，具体的代码如下：

输入数据是向量，标签是标量（1,0），这种是比较简单的一种情况。用带有relu 激活的全连接层（Dense）的简单堆叠，比如 Dense(16, activation='relu')就比较好。16是该层隐藏单元的个数，一个隐藏单元（hidden unit）是该层表示空间的一个维度。

16 个隐藏单元对应的权重矩阵 W 的形状为 (input_dimension, 16)，与 W 做点积相当于将输入数据投影到16 维表示空间中（然后再加上偏置向量 b 并应用 relu 运算）。你可以将表示空间的维度直观地理解为“网络学习内部表示时所拥有的自由度”。隐藏单元越多（即更高维的表示空间），网络越能够学到更加复杂的表示，但网络的计算代价也变得更大，而且可能会导致学到不好的模式（这种模式会提高训练数据上的性能，但不会提高测试数据上的性能）。

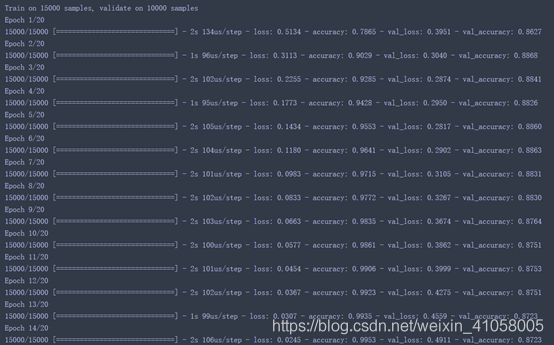
最后，你需要选择损失函数和优化器。由于你面对的是一个二分类问题，网络输出是一个概率值（网络最后一层使用sigmoid 激活函数，仅包含一个单元），那么最好使用 binary_ crossentropy（二元交叉熵）损失。这并不是唯一可行的选择，比如你还可以使用mean_squared_error（均方误差）。但对于输出概率值的模型，交叉熵（crossentropy）往往是最好的选择。交叉熵是来自于信息论领域的概念，用于衡量概率分布之间的距离，在这个例子中就是真实分布与预测值之间的距离。代码如下所示

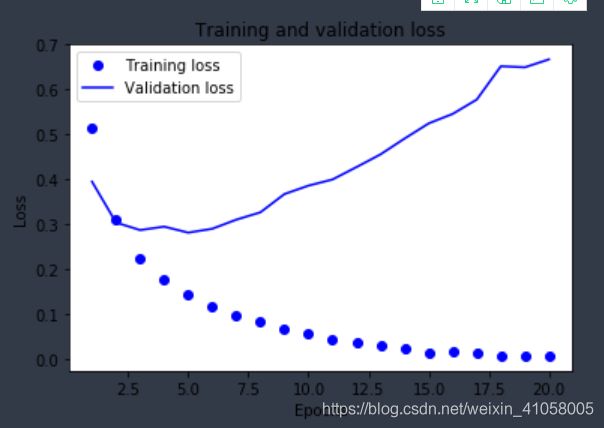
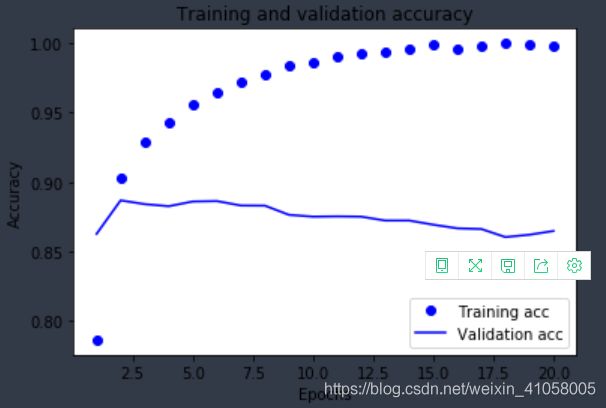
根据数据可以发现，在训练集的精度逐渐上升，但是到了验证集，只有87%

这个实验就差不多了，实际上，训练20轮的结果还有些下降，不如在训练4轮之后停止训练，验证集还有88%的正确率。主要是要记住网络构建的大体结构

 

多分类问题：新闻分类

将路透社新闻划分为46个互斥的主题，单标签，多分类的问题；

要是可以将每个数据点划分到多个类别，就是多标签、多分类问题

之前下好了数据集，整个流程变得方便多了

将标签向量化有两种方法：你可以将标签列表转换为整数张量，或者使用one-hot 编码。 one-hot 编码是分类数据广泛使用的一种格式，也叫分类编码（categorical encoding）

 

回归问题：预测房价

这个数据集也已经下好，按照示例程序可以轻松实现，这里不再做实验，不同之处在于引入了K折验证：

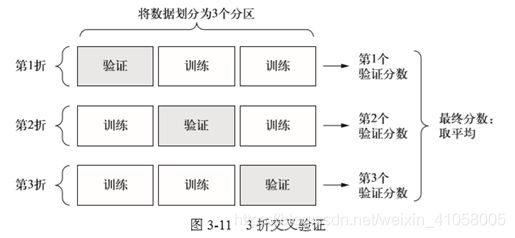
为了在调节网络参数（比如训练的轮数）的同时对网络进行评估，你可以将数据划分为训练集和验证集，正如前面例子中所做的那样。但由于数据点很少，验证集会非常小（比如大约 100个样本）。因此，验证分数可能会有很大波动，这取决于你所选择的验证集和训练集。也就是说，验证集的划分方式可能会造成验证分数上有很大的方差，这样就无法对模型进行可靠的评估。 在这种情况下，最佳做法是使用 K 折交叉验证（见图 3-11）。这种方法将可用数据划分为 k个分区（K 通常取 4 或 5），实例化K个相同的模型，将每个模型在 K-1个分区上训练，并在剩下的一个分区上进行评估。模型的验证分数等于K个验证分数的平均值。这种方法的代码实现很简单。

回归常用的损失函数是均方误差（MSE），评估指标比较常见的是平均绝对误差（MAE）