支持向量机原理推导学习

SVM（Support Vetcor Machine），解决二分类问题的好方法，也可以用来解决多分类问题。写程序的重点应该在SMO这里，个人觉得SVM的原理还是算比较难的，虽然本人也算90%的数学科班出身。原理刚开始看书的时候没怎么看懂，后来听老师讲了一遍，很可惜也没讲具体的推导过程，就下来上网搜了搜。以下是学习过程中的手写笔记，内容还算明了，适合机器学习新手阅读。

最后半页纸，其实算是SVM的小拓展，就是给优化函数加了个正则项，感觉更广泛应用于实际问题中。

 

 

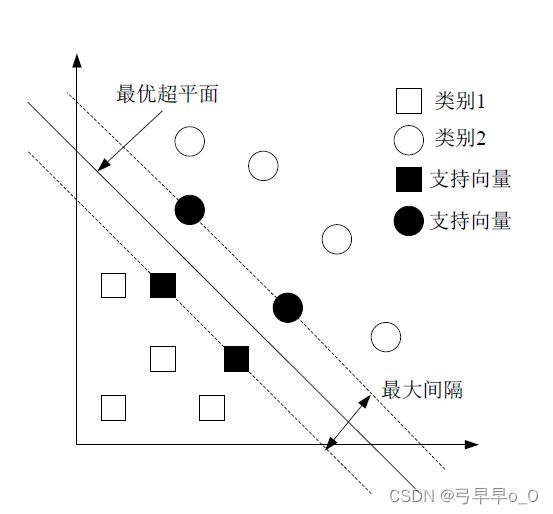
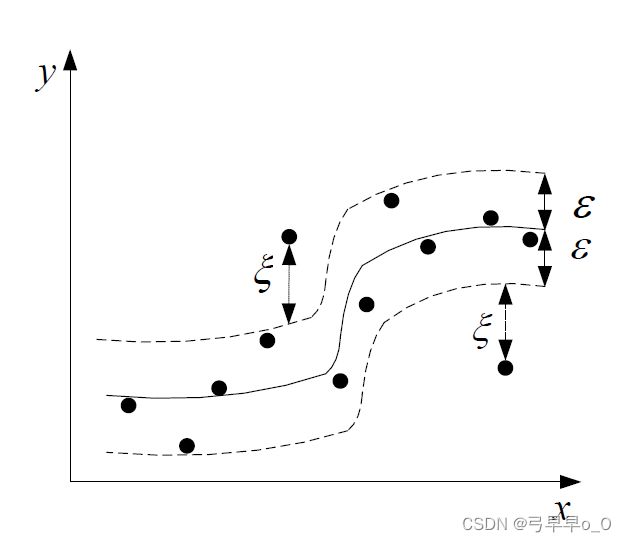
SVM解决分类问题，对应的SVR(Support Vector Regression)可解决回归问题。分类问题实质上就是用个超平面把两类样本分来。具体实现的话，是用一种叫支持向量的东西，其实就是距离超平面比较近的样本。实现目标是样本的误判率较低，也就是正确率高。回归问题和分类比较类似，它的目标是预测的回归值和原始回归值之间的误差最小。下面两个图分别是SVM和SVR的图示。

上次做了个题，用的是SVR，五个特征拟合一个y，但是那个结果不怎么好。

下面附代码： 

import processing
from sklearn.svm import SVR
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn import preprocessing
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score
import matplotlib.pylab as pl
import warnings
warnings.filterwarnings('ignore')
MSE = 0
R2 = 0
for i in range(0,500):
    x, y_10cm, y_40cm, y_100cm, y_200cm = processing.loadData('water.xlsx')
    # 划分训练集/测试集
    X_train, X_test, Y_train, Y_test = train_test_split(x, y_10cm, test_size=0.3)
    X_train = np.array(X_train).reshape(86, 5)
    X_test = np.array(X_test).reshape(37, 5)
    Y_train = np.array(Y_train).reshape(86, 1)
Y_test = np.array(Y_test).reshape(37, 1)
# 数据归一化
mms = preprocessing.MinMaxScaler()
X_train_mms = mms.fit_transform(X_train)
X_test_mms = mms.transform(X_test)
Y_train_mms = mms.fit_transform(Y_train)
# 建立SVR模型
svm = SVR(kernel='rbf', degree=3, gamma='auto',
            coef0=0.0, tol=1e-5, C=1.0, epsilon=0.1, shrinking=True,
           cache_size=200, verbose=False, max_iter=-1)
# 训练SVR模型
    svm.fit(X_train_mms, Y_train_mms)
# SVR模型预测
    Y_sim_mms = svm.predict(X_test_mms)
# 反归一化
    Y_sim = mms.inverse_transform(Y_sim_mms.reshape(37, -1))
# 结果
    Result = np.hstack((Y_test, Y_sim))
    MSE += mean_squared_error(Y_test, Y_sim)
    R2 += r2_score(Y_test, Y_sim)
print(Result)
print('Prediction Average Mean Squared Error (MSE) is {:f}'.format(MSE/500))
print('Prediction Average Determined Coefficient R2 is {:f}'.format(R2/500))
# 绘图
pl.rcParams['font.sans-serif']=['SimHei']
pl.rcParams['axes.unicode_minus'] = False
pl.figure()
pl.scatter(Y_test, Y_sim)
pl.xlabel('真实值')
pl.ylabel('预测值')
pl.title('土壤湿度预测结果（R2={:f})'.format(R2/500))
pl.plot(Y_test, Y_test, 'r')
pl.show()

下面是在5个特征里面通过随机森林筛选重要特征的代码：

import pandas as pd
import processing
from sklearn.ensemble import RandomForestRegressor
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error,mean_absolute_error
import warnings
from sklearn import preprocessing
warnings.filterwarnings('ignore')
x, y_10cm, y_40cm, y_100cm, y_200cm = processing.loadData('water.xlsx')
X_train, X_test, Y_train, Y_test = train_test_split(x, y_10cm, test_size=0.2)
X_train = np.array(X_train).reshape(98, 5)
X_test = np.array(X_test).reshape(25, 5)
Y_train = np.array(Y_train).reshape(98, 1)
Y_test = np.array(Y_test).reshape(25, 1)
# 数据归一化
mms = preprocessing.MinMaxScaler()
X_train_mms = mms.fit_transform(X_train)
X_test_mms = mms.transform(X_test)
Y_train_mms = mms.fit_transform(Y_train)
Y_test_mms = mms.transform(Y_test)
# 建立随机森林模型
forest = RandomForestRegressor(
    n_estimators=100,
    random_state=1,
 n_jobs=1
)
# 训练随机森林模型
forest.fit(X_train_mms, Y_train_mms)
Y_sim_mms = forest.predict(X_test_mms)
# 反归一化
Y_sim = mms.inverse_transform(Y_sim_mms.reshape(25, -1))
score = forest.score(X_test_mms,Y_test_mms)
print('随机森林模型得分： ', score)
print('Mean Absolute Error:', mean_absolute_error(Y_sim,Y_test))
print('Mean Squared Error:', mean_squared_error(Y_sim,Y_test))
print('Root Mean Squared Error:', np.sqrt(mean_squared_error(Y_sim,Y_test)))
# 描述模型特征重要性
X_train = pd.DataFrame(X_train)
col = list(X_train.columns.values)
importances = forest.feature_importances_
x_columns = ['植被指数(NDVI)','土壤蒸发量(mm)','低层植被(LAIL,m2/m2)','放牧强度','降水量(mm)']
indices = np.argsort(importances)[::-1]
list01=[]
list02=[]
for f in range(X_train.shape[1]):
    print(("%2d) %-*s %f" % (f + 1, 30, col[indices[f]], importances[indices[f]])))
    list01.append(col[indices[f]])
    list02.append(importances[indices[f]])
from pandas.core.frame import DataFrame
c = {"columns": list01, "importances": list02}
data_impts = DataFrame(c)
data_impts.to_excel('data_importances.xlsx')
importances = list(forest.feature_importances_)
feature_list = list(X_train.columns)
feature_importances = [(feature, round(importance, 2)) for feature, importance in zip(feature_list, importances)]
feature_importances = sorted(feature_importances, key=lambda x: x[1], reverse=True)
import matplotlib.pyplot as plt
x_values = list(range(len(importances)))
print(x_values)
plt.bar(x_values, importances, orientation='vertical')
plt.xticks(x_values, feature_list, rotation=6)
plt.ylabel('Importance')
plt.xlabel('Variable')
plt.title('Variable Importances')
plt.show()

SVM的原理还需要继续学习，要流畅到可以给别人脱稿讲的程度。今天把BP神经网络的原理搞懂了，下次文章发BP原理推导。