【线性代数】最小二乘法的本质、施密特正交化的“前世今生”,投影的核心思想
目录
一、处理无解线性方程组
1.1 解线性方程组无解的几何意义
1.2 寻求线性方程组的近似解
1.3 利用矩阵描述向一维直线的投影
1.4 利用Python计算无解线性方程组的近似解
二、 深入剖析最小二乘法的本质
2.1 互补的子空间,正交的子空间,互补正交的子空间
2.2 最小二乘法线性拟合
三、 施密特(Schmidt)正交化:寻找最佳投影基
3.1 简化投影计算
3.2 标准正交向量
3.3 施密特(Schmidt)正交化
3.4 使用Python正交化三维向量
四、 总结一下
一、处理无解线性方程组
1.1 解线性方程组无解的几何意义
在工作和生活中,我们常常发现,并不是每一个问题都有一个精确的解,数学问题也存在这种情况。线性方程组解的问题,它可能有解,也可能无解。此时我们无法寻找到事物的真相,但我们可以尽量让自己站在离真相最近的地方去观察这个问题。换句话说,就是尽量寻找问题的近似解。
问题引入:解线性方程组
显然这个线性方程组无解,无解的原因是向量
不在矩阵
的列空间(Column Space)中,(列空间(Column Space)是系数矩阵A各列向量所有线性组合结果的集合,即系数矩阵A所张成的向量空间),对于矩阵方程AX=b,向量b是否在系数矩阵A张成的列空间中是判断线性方程组是否有解的充分必要条件,也是线性代数的重要核心思想之一,关于列空间的介绍,详见之间的文章,肝三个通宵万字写的 线代的基础知识
线性方程组列空间如下图所示如下图所示。
图中col1是系数矩阵A第一列的列向量,col2是第二列的列向量,它们张成的向量空间是一个过原点的二维平面,在图中用虚线表示,很明显向量b不在向量col1和col2张成的向量空间中,方程组无解。
1.2 寻求线性方程组的近似解
线性方程组无解,但是,我们不仅仅只停留于无解的这个基本结论中,我们知道两点之间直线线距离最短,那么向量b与平面之间的最短距离如何寻找呢?答案就是投影,即向量b向平面的投影。
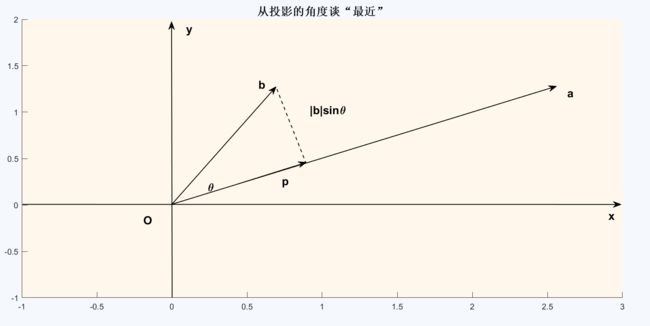
首先,我们如何定义和描述“距离最近”呢?我们看一个问题:
在二维平面中,有一条穿过原点的直线,并且这条直线沿着向量a的方向。在空间中还有一个点b,那么如何在这条直线上找到一个点,使得这个点距离b最近?解决方法是通过点b向已知的直线做一条垂线,这样就能获得我们想要的最短距离,如下图所示:
向量b和向量a的夹角是![]() ,因此,通过点b到直线的最近距离可以表示为
,因此,通过点b到直线的最近距离可以表示为![]() ,向量p是向量b在向量a上的投影向量,我们把b到向量a构成的向量记作e,e也称为误差向量,对于向量
,向量p是向量b在向量a上的投影向量,我们把b到向量a构成的向量记作e,e也称为误差向量,对于向量![]() ,它的长度
,它的长度![]() 就是我们寻找的最近距离。
就是我们寻找的最近距离。
1.3 利用矩阵描述向一维直线的投影
如果将向量a作为这条直线的基向量,那么p就可以用向量a来表示,p=xa(x是一个标量,即标量系数)。因为误差向量e与a垂直,所以有:ae=0
从表达式来看,标量系数x是向量a与b的点积除以向量a与a的点积,即内积(Inner Product)。根据内积的几何意义,向量a与b内积的几何意义是向量b在向量a上的投影长度乘以向量a的模长,向量a与a的内积的几何意义是a的模长乘以a的模长(因为![]() ),那么标量系数的比值意义就很明显了。
),那么标量系数的比值意义就很明显了。
从矩阵的意义来理解,因为![]() ,所以标量系数x可以写为
,所以标量系数x可以写为![]() ,那么投影向量
,那么投影向量![]() .我们知道,矩阵的本质是映射,在矩阵的作用下,将点b映射到点p,那么这个映射矩阵是什么呢?这里有一个小技巧,因为p=xa,x是一个标量,所以
.我们知道,矩阵的本质是映射,在矩阵的作用下,将点b映射到点p,那么这个映射矩阵是什么呢?这里有一个小技巧,因为p=xa,x是一个标量,所以
那么,投影矩阵![]() ,至此关于投影,三个重要的关系式就推导出来了。再推广到n维向量空间中,标量系数x,投影向量p和投影矩阵P的关系式如下(推导原理是一样的,这里就不做推到了):
,至此关于投影,三个重要的关系式就推导出来了。再推广到n维向量空间中,标量系数x,投影向量p和投影矩阵P的关系式如下(推导原理是一样的,这里就不做推到了):
再回到我们上面解线性方程组的话题上,因为线性方程组向量b不在系数矩阵A张成的向量空间中,因此线性方程组无解,我们把问题转化为寻求向量b在系数矩阵A张成的空间中最近的一个向量,即投影向量p,用它来表示方程组的近似解。根据我们上面的推导,投影向量
如下图所示:
在三维向量空间中,我们寻找向量b在系数矩阵A张成的向量空间中的投影向量p,根据公式 ![]()
那么方程组的近似解为
1.4 利用Python计算无解线性方程组的近似解
import pandas as pd
import numpy as np
A=np.mat([[2,1],[1,2],[1,4]])
b=np.mat([[4],[3],[9]])
#计算标量系数
x=np.linalg.inv(A.T*A)*A.T*b
#计算投影向量
p=A*np.linalg.inv(A.T*A)*A.T*b
#计算投影矩阵
P=A*np.linalg.inv(A.T*A)*A.T
print(f"标量系数x为:{x}")
print(f"投影向量p为:{p}")
print(f"投影矩阵P为:{P}")输出结果为:
标量系数x为: [[0.83870968] [1.87096774]] 投影向量p为: [[3.5483871 ] [4.58064516] [8.32258065]] 投影矩阵P为: [[ 0.93548387 0.22580645 -0.09677419] [ 0.22580645 0.20967742 0.33870968] [-0.09677419 0.33870968 0.85483871]]
这与我们的计算结果是一致的,当然通过投影的方式不仅仅可以用来解线性方程组,还可以揭示最小二乘法的本质。
二、 深入剖析最小二乘法的本质
对于最小二乘法,大家肯定不陌生,但是,何为最小二乘法呢?最小二乘法解决的是什么问题?通过投影的思想来寻求线性方程组的解与最小二乘法有什么关系?兄弟们,快要到了揭示真相的时刻了,快冲。
2.1 互补的子空间,正交的子空间,互补正交的子空间
在![]() 空间中有一个向量b,可以选取m个线性无关的向量
空间中有一个向量b,可以选取m个线性无关的向量![]() ,作为
,作为![]() 空间的一组基向量,将b向基向量投影,就能得到m个投影向量:
空间的一组基向量,将b向基向量投影,就能得到m个投影向量:![]() ,并且它们满足:
,并且它们满足:![]() ,即通过空间上所有投影轴上的投影向量能够重构向量的完整信息。
,即通过空间上所有投影轴上的投影向量能够重构向量的完整信息。
对于上面的说法可能有些专业,但是,兄弟们,学习线代这门课程,要懂“搞基”的艺术,并且遵循“三讲”的要领,即,讲思想,讲方法,讲艺术。引用大佬的话来讲,“从行列式开始的线代都是毒教材”,过于精炼化,公式化不便于理解。在强调一遍矩阵乘法的第一核心思想,
映射前后,列向量x的基向量维数都发生了变化,原始的n为列向量x被变换成了n个m维的列向量线性组合的形式。最终的运算结果是一个m维的列向量。
再用一句话概括,矩阵与向量乘法的本质是变换原始向量的基底,将默认基底变换为矩阵A的各列,由矩阵A的各列充当目标向量新的基向量,在结合原始向量的坐标,最终到目标向量目标空间的位置。
用这个思想来理解互补子空间的概念,不用多讲了吧!!!
再举个例子:
概括的说,互补的子空间一方面由不同的基向量所张成,另一方面它们的维数之和为整个R^m空间的维数。
正交的子空间
子空间V和子空间W满足正交关系成立的条件是:子空间V中任意一个向量v和子空间W中任意一个向量w都垂直。
互补正交的子空间
![]() 空间中两个互补的子空间,如果满足相互正交的关系,则它们满足正交补的关系,它们的空间维数之和为m.那么如何寻找正交补子空间呢?
空间中两个互补的子空间,如果满足相互正交的关系,则它们满足正交补的关系,它们的空间维数之和为m.那么如何寻找正交补子空间呢?
行空间和零空间是正交子空间,行空间和零空间满足正交补的关系.
转置矩阵![]() 的行空间和零空间当然也是相互正交的,因此矩阵的列空间和左零空间在
的行空间和零空间当然也是相互正交的,因此矩阵的列空间和左零空间在![]() 中同样满足正交补的关系。
中同样满足正交补的关系。
这几个概念理解了好,理解不了也不要紧,下面上“硬菜”。
2.2 最小二乘法线性拟合
何为最小二乘法?最小二乘法就是最小平方的意思。举个例子吧。
在平面上选取三个点:(0,1),(1,4),(2,3)找一条最接近着三个点的直线,设直线方程为![]() ,那么则有:
,那么则有:
显然,方程组是无解的,令矩阵
向量
转换为矩阵乘法的形式为
是不是很神奇呢?换个频道,回到投影的思想方法,二维向量空间中的三个点,即就是平面内的三个点,要找到一条直线距离这三个点的距离最近,怎么找呢?讲了这么多投影肯定是投影了,三个点分别向直线投影,投影的距离最小,那距离最小了,是不是就最小二乘法了,最小平方了。到了此处,再问一句,最小二乘法的本质是什么呢?答案是投影。
再来总结一下,投影解决的两个问题,寻求线性方程组的近似解和揭秘最小二乘法的本质。
显然,投影并不局限于此,在寻求线性方程组的时候,对于标量系数x,投影向量p和投影矩阵P的公式辣么长,在没有窥探到事物的本质前,你能记得住?显然你记不住,时间长了我也记不住,(其实理解了标量系数x也简简单单)。就算记住了,公式中涉及求矩阵乘法和逆矩阵的运算只适合电脑运算,不适合人脑运算。那么有没有一种方法,可以简化标量系数的公式和运算方法呢?答案是肯定的,那方法是什么呢?答案也是肯定的,还是投影。
三、 施密特(Schmidt)正交化:寻找最佳投影基
有人说,施密特(Schmidt)正交化是线代里面最难记的公式之一,公式是长一些,但是在“搞基”艺术和“三讲思想”的指导下还是可以简简单单的。
3.1 简化投影计算
投影向量![]() 将空间中的任意一个向量向任意子空间进行投影,并最终得到投影向量p.其中矩阵A的各列对应子空间的一组基向量.
将空间中的任意一个向量向任意子空间进行投影,并最终得到投影向量p.其中矩阵A的各列对应子空间的一组基向量.
思路:![]() 相乘的结果是一个单位矩阵就好了,因为单位矩阵满足
相乘的结果是一个单位矩阵就好了,因为单位矩阵满足![]() ,投影向量p的表达式就为
,投影向量p的表达式就为![]() .
.
3.2 标准正交向量
令矩阵
![]()
各列向量![]() 彼此之间线性无关,因此就可以构成R^n空间的一组基.
彼此之间线性无关,因此就可以构成R^n空间的一组基.
要得到![]() 的最终结果为I,则列向量必须满足一下两个条件:
的最终结果为I,则列向量必须满足一下两个条件:
(1)在结果矩阵中,对角线上的元素必须都为1,即当i=j时,![]() .
.
(2)在结果矩阵中,非对角线上的元素必须都为0,即当i\ne j时,![]() .
.
直白的说,列向量![]() 彼此之间的点积为0,意味着向量之间标准正交;而向量与自身的点积为1,意味着向量的模长为1,这一组单位向量均为列向量,我们称这一组列向量是标准正交的。由一组标准正交的向量
彼此之间的点积为0,意味着向量之间标准正交;而向量与自身的点积为1,意味着向量的模长为1,这一组单位向量均为列向量,我们称这一组列向量是标准正交的。由一组标准正交的向量![]() 构成的各列矩阵,一般用字母Q表示,此时矩阵Q满足
构成的各列矩阵,一般用字母Q表示,此时矩阵Q满足![]() 关系成立.当矩阵Q是一个方阵时,我们称方阵Q是正交矩阵,并且方阵Q满足可逆性。
关系成立.当矩阵Q是一个方阵时,我们称方阵Q是正交矩阵,并且方阵Q满足可逆性。
这时,方阵Q具备一个有趣的性质:![]() .即,正交矩阵的逆矩阵等于自身的转置矩阵。
.即,正交矩阵的逆矩阵等于自身的转置矩阵。
使用正交矩阵Q代替矩阵A,由于![]() ,投影矩阵p和投影向量p的表达式都得以简化:
,投影矩阵p和投影向量p的表达式都得以简化:
3.3 施密特(Schmidt)正交化
如果上面你还看得似懂非懂,不要紧,我们直直白白的讲一下什么是施密特正交化,为什么要正交化?
啥是正交呢?简简单单的讲就是相互垂直,就是把两个或者多个不相互垂直的向量(即彼此之间线性无关)变成垂直的向量,再把它们单位化就OK了。提到垂直,你疲惫的小神经有没有泛起一丝涟漪呢?有没有一丝的感觉呢?一个向量向另一个向量投影,前面提到的误差向量e是不是和向量a垂直,向量b,投影向量p和误差向量e是首尾相接的,那么,那么,正交化的思路???你有了吗???
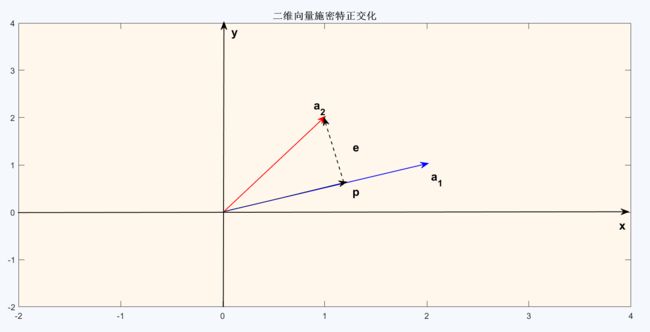
接上面的例子来实例化吧:
给定两个二维向量
求标准正交向量![]()
通过我们上面的分析,在二维向量空间中,其实就是先确定定向量![]() ,即
,即
![]()
求误差向量e,然后把向量e和向量![]() 单位化(单位化就是把向量变为模长为1的向量,即就是
单位化(单位化就是把向量变为模长为1的向量,即就是![]() ),那么,从内积的角度来理解标量系数x,向量e为:
),那么,从内积的角度来理解标量系数x,向量e为:
即就是
再把它们标准化,我们就得到了一组标准正交的基向量。
答案应该很清楚了,施密特标准正交化的核心是投影。
二维平面内正交化的公式出来了,那n维向量空间如何正交化呢?原理是一样的,给一下你们公式,自己悟吧,实在悟不清楚找我哈。
最后,通过公式计算完后,一定记得单位化,单位化,单位化,不要掉坑里了。
3.4 使用Python正交化三维向量
设
使用施密特正交将这组向量正交化。
import numpy as np
a1=np.array([1,2,-1])
a2=np.array([-1,3,1])
a3=np.array([4,-1,0])
A=np.array([[1,-1,4],[2,3,-1],[-1,1,0]])
a11=a1
a22=a2-np.dot(a1,a2)/np.dot(a1,a1)*a1
a33=a3-np.dot(a1,a3)/np.dot(a1,a1)*a1-np.dot(a2,a3)/np.dot(a2,a2)*a2
print(a11,a22,a33)
print(a11/np.linalg.norm(a11))
print(a22/np.linalg.norm(a22))
print(a33/np.linalg.norm(a33))输出结果为:
正交基: [ 1 2 -1] [-1.66666667 1.66666667 1.66666667] [3.03030303 0.24242424 0.96969697] 正交基单位化: [ 0.40824829 0.81649658 -0.40824829] [-0.57735027 0.57735027 0.57735027] [0.94967147 0.07597372 0.30389487]
四、 总结一下
思想指导行动,先总结一下思想:
“搞基”核心思想一:线性方程组Ax=b有解的充分必要条件是,向量b在系数矩阵A张成的列空间(Column Space)上。
“搞基”核心思想二:矩阵与向量乘法的本质是变换原始向量的基底,将默认基底变换为矩阵A的各列,由矩阵A的各列充当目标向量新的基向量,在结合原始向量的坐标,最终到目标向量目标空间的位置。
“搞基”核心思想三:在空间中,距离最近的是投影,最小二乘法的本质还是投影。
“搞基”核心思想四:施密特正交化的公式真的不难记,重在理解,哈哈哈!
今天的分享到此为止,感谢各位“基友”的阅读,文章可能还有很多不足之处,请多指教。如果对您有所收获,有所感悟,有所疑惑,记得收藏、点赞、评论,瑞思拜!

![\left[\begin{array}{cc}2&1\\1&2\\1&4\\\end{array}\right]](http://img.e-com-net.com/image/info8/a40cfb56124e4b3fa8b4da1f76acd976.gif)





![b=\left[\begin{array}{cc}1\\2\\3\\\end{array}\right]](http://img.e-com-net.com/image/info8/8c8c5304c0dc44b1bb13824acc6b7991.gif)

![A=\left[\begin{array}{cc}0&1\\1&1\\2&1\\\end{array}\right],](http://img.e-com-net.com/image/info8/afaad6fa59fb49c0bb129dbaa21c5109.gif)
![b=\left[\begin{array}{cc}1\\4\\3\\\end{array}\right]](http://img.e-com-net.com/image/info8/59efae58745c4765975aed90fb58f95c.gif)

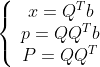
![a_1=\left[\begin{array}{cc}1\\2\\-1\\\end{array}\right],a_2=\left[\begin{array}{cc}-1\\3\\1\\\end{array}\right],a_3=\left[\begin{array}{cc}4\\-1\\0\\\end{array}\right]](http://img.e-com-net.com/image/info8/d9ef159907424868a45aec4ddba95e33.gif)