差分数组+两个简单例子

目录

1.什么是差分数组？

2.差分数组怎么求

差分数组能干啥

差分数组怎么用:

例1:HDU-1556 Color the Ball  Problem - 1556

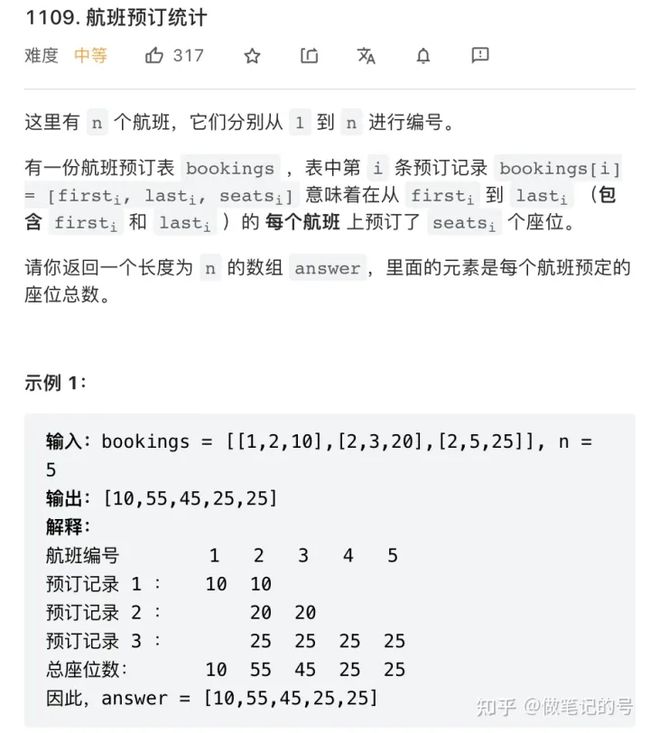
例2:   1109. 航班预订统计

3.差分数组的性质:

---

 

1.什么是差分数组？

从字面上解释，差分数组就是记录一个数组的前后元素之差的数组，例如：

有数组nums的内容如下：

0	1	2	3	4	5
2	4	1	5	8	10

那么数组nums的差分数组diff就是：

        0	1	2	3	4	5
nums	2	4	1	5	8	10
diff	2	2	-3	4	3	2

数组diff的长度和原数组nums一样，其中diff[0]默认为nums[0]，其它

diff[i] = nums[i] - nums[i-1]

1.差分数组的特点一：

当我们需要在长度很大的原数组的某个区间做频繁的统一运算操作时，可以不操作原数组，而是直接计算其差分数组以提高效率。举个简单的例子，现在需要将上面数组nums的[1, 3]区间元素都累加2，则结果如下：

        0	1	2	3	4	5
nums	2	4+2	1+2	5+2	8	10
diff	2	2+2	-3	4	3+(-2)	2

所以对原数组某个区间的操作只会影响差分数组中两个元素的值，如果区间是[i,j]，那么只会影响差分数组的i和j+1两个元素

2.差分数组的特点二：

d[i] = f[0] + f[1] + … + f[i]

即用差分数组的前i项和可以求得原数组的第i个元素的值！

nums[3] = 7 = diff[0] + diff[1] + diff[2] + diff[3] = 2 + 4 - 3 + 4 = 7

差分其实就是数据之间的差，什么数据的差呢？就是上面所给的原始数组的相邻元素之间的差值，我们令 d[i]=a[i+1]-a[i]，一遍for循环即可将差分数组求出来。

下面给你一个栗子，给出一个差分数组先

2.差分数组怎么求

其实差分数组是一个辅助数组，从侧面来表示给定某一数组的变化，一般用来对数组进行区间修改的操作

还是上面那个表里的栗子，我们需要进行以下操作：

1、将区间【1，4】的数值全部加上3

2、将区间【3，5】的数值全部减去5

很简单对吧，你可以进行枚举。但是如果给你的数据量是1e5，操作量1e5，限时1000ms你暴力枚举能莽的过去吗？T到你怀疑人生直接。这时我们就需要使用到差分数组了。

其实当你将原始数组中元素同时加上或者减掉某个数，那么他们的差分数组其实是不会变化的。

利用这个思想，咱们将区间缩小，缩小的例子中的区间 【1,4】吧这是你会发现只有 d[1]和d[5]发生了变化，而d[2],d[3],d[4]却保持着原样，

在进行下一个操作，

这时我们就会发现这样一个规律，当对一个区间进行增减某个值的时候，他的差分数组对应的区间左端点的值会同步变化，而他的右端点的后一个值则会相反地变化，其实这个很好理解

其实也就这么一点代码就ok了

1. while(m--){//操作次数

2. cin>>left>>right>>change;//左右端点及其变化的值

3. d[left]+=change;

4. d[right+1]-=change;

5. }

差分数组能干啥

既然我们要对区间进行修改，那么差分数组的作用一定就是求多次进行区间修改后的数组喽

注意 只能是区间元素同时增加或减少相同的数的情况才能用

因为我们的差分数组是由原始数组的相邻两项作差求出来的，即 d[i]=a[i]-a[i-1]；那么我们能不能反过来，求得一下修改过后的a[i]呢？

直接反过来即得  a[i]=a[i-1]+d[i] 

事实证明这是正确的，具体证法就不再推广，有空再补上吧；

更新数组a的方式则是下面的那一点点代码，这样我们就求出来了更新后的数组 a，是不是比线段树快多了呢？

1. for(int i=1;i<=n;i++)

2. a[i]=a[i-1]+b[i];

差分数组怎么用:

翻来覆去还是那句，区间修改，当然了，有时候要结合树状数组来使用。直接看题目吧

例1:HDU-1556 Color the Ball  Problem - 1556

这个题果的不能再果了吧，看懂上面的，闭着眼也能敲出来

直接附上代码吧

#include
#include
#include
#include
#include
#include
#define ll long long
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
const int inf=0x3f3f3f3f;
const int mm=1e5+10;
 
int a[mm],b[mm];
int x,y;
int main()
{
    int n;
    while(scanf("%d",&n)&&n){
        mem(a,0);
        mem(b,0);
        for(int i=1;i<=n;i++){
            scanf("%d%d",&x,&y);
            b[x]++;
            b[y+1]--;
        }
        for(int i=1;i<=n;i++)
            a[i]=a[i-1]+b[i];
       
        for(int i=1;i

例2:   1109. 航班预订统计

在遍历bookings数组的过程中，我们需要对返回的答案数组不断的做区间增量修改，因此可以使用差分数组来求解。

3.差分数组的性质:

当我们希望对原数组的某一个区间[l,r]施加一个增量inc时，差分数组d对应的变化是：d[l]增加inc，d[r+1]减少inc，并且这种操作是可以叠加的。

例如：有数组d=[1,2,3,4,5,6]，对d[2]到d[4]之间的所有数加上3，变为d=[1,2,6,7,8,6]，那么差分数组也就从[1,1,1,1,1,1]变成了[1,1,4,1,1,-2]。

也就是说，当我们需要对原数组的不同区间施加不同的增量，我们只要按规则修改差分数组即可。