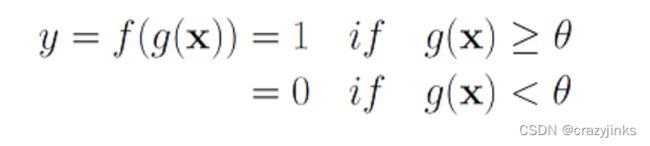一文带你读懂感知机的前世今生(上)

前言

男女不分

朋友， 当你看到类似下图的这样一副图像， 你有十足的信心区分出这是男性或者是女性吗?， 看上去相貌很像男性(尽管我们自己说不出来什么是我们自己认为的男性相貌特征)，但是佩戴的耳环又让这个问题显得困惑。
是什么导致了这种现象的发生呢? 我们的判断来自大脑认知的结果。是神经元工作的产物。接下来让我们粗浅地了解一下什么是神经元。

什么是神经元

神经元实现了对环境的感知和信息的传递.虽然神经元形态与功能多种多样，但结构上大致都可分成细胞体（cell body， or soma）和神经突两部分。神经突又分树突（Dendrites）和轴突（Axon）两种。轴突很细， 以一毫米的千分之一(μm)微米做直径单位， 轴突很长，最长可达1m，轴突由细胞的轴丘（axon hillock）分出，开始一段称为始段，离开细胞体一段距离后始获得髓鞘(它可以加速信号传递，并保护轴突)，成为神经纤维。
细胞体的大小差异很大，小的直径仅5～6μm，大的可达100μm以上。突起的形态、数量和长短也很不相同。树突多呈树状分支，它可接受刺激并将神经冲动（Nerve Impulse）传向胞体，我们把它理解成输入过程；胞体完成信息的处理， 然后在轴丘部分按照All-or-Non(全无或有)的法则产生刺激. 然后通过一个细索状的轴突，将神经冲动（Nerve Impulse）从胞体传向轴突终末（axon terminal）， 轴突末和向其他神经元或效应细胞相接触， 接着类似的活动在下一个神经元继续发生， 由此神经元实现了信息的处理和传递。
通常一个神经元有一个至多个树突，但轴突只有一条。神经元的胞体越大，其轴突越长。

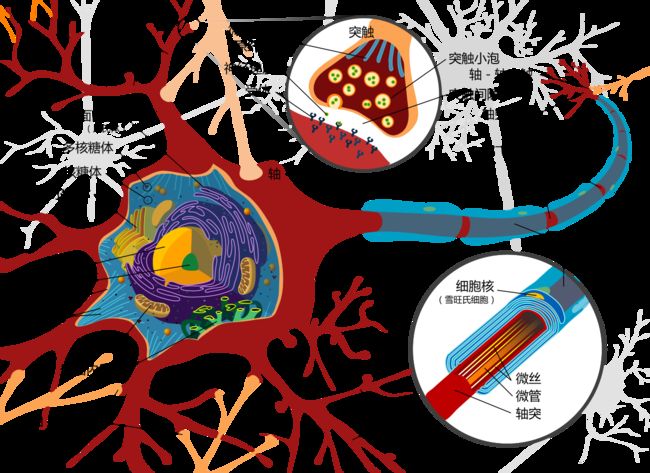
[注: hhh ，没有被吓到吧. 当然， 这个图片包含了太多不必要的细节，咱们现在只需要只到树突， 细胞体，轴丘，轴突， 突触在哪里，你能找到吗?]

根据细胞体凸起的数量不同，我们将神经元分为4类。它们叫做单极神经元， 双极神经元， 多级神经元以及伪单极神经元。

1: Unipolar neuron 单极神经元
主要存在于无脊椎动物体内–比如刺胞动物（水母，珊瑚），海洋蠕虫，软体动物（蜗牛），节肢动物（螃蟹，虾，龙虾）和棘皮动物（海星，海胆）等，其种类数占动物总种类数的95%。无脊椎动物中枢神经系统中的神经元大都是单极神经元。

2: Bipolar neuron 双极神经元
主要存在于视听系统内(见视网膜双极细胞，前庭神经)

3: Multipolar neuron 多极神经元
我们大脑中的神经元就多数都是这种多级神经元， 是我们接下来要讨论的重点， 也是梦开始的地方。

4: Pseudounipolar neuron 伪单极神经元
你可以想象这种神经元就住在我们的脊柱附近，它从细胞体(Soma)长出一个突起，然后这个突起分为两支，一只伸向外周神经系统的称周围突（peripheral process），它涵盖了多种感受器(Sensory receptor)，用来接受外界的刺激(用作输入)。 然后一只伸向我们的中枢神经系统，称为中央突(用于输出)。 比如磕着膝盖疼，就是它在告诉你，我很重地碰着了膝盖(某种外界压力的信息)，然后你的中枢神经收到信息说，也，这怕是有点痛哦! 然后做下一步行动， 比如执行’哭’或者其它行为。

我们来简要总结一下

神经元种类	树突	轴突
单极神经元	0	1
双极神经元	1	1
多极神经元	>1	1
*伪单极神经元	0	轴突呈T型一分为2(外周突，中央突)

*注:你也可以认为伪单极神经元是拥有1个树突的， 因为伸向器官皮肤的周围突接受刺激，但是因为它形态上和轴突没有显著区别，所以你可以选择你一种喜欢的说法来称呼它，树突 | 轴突，都可以。 本文暂将其一并称为轴突

M-P神经元

全或无定律

好的，我们刚才仿佛上了一个强化班， 学习了很多神经科学的知识。可是， 这和我们今天说的感知机有什么关联呢。实际上人工智能学科的发展在历史上也离不开神经科学等学科的发展。上述经验是经过很多代神经科学发展才认识到的。
比如神经传导的一项基本特性全或无定律(all-or-none law)，
是鲍迪奇(Bowditch)于1871年研究心肌时首先发现，是神经传导的一项基本特性。就是给神经元的刺激需要达到一定的强度，神经元才会被激活(开始传递冲动)，如果达不到就完全不激活，要么有要么完全没有。后来其他学者发现它对轴突也同样适用。我们取一个伪单极神经元来做例子(还记得它的结构吗)。 比如我们磕着膝盖了， 就是皮肤下的感受器(Sensory receptor)把信号给神经元细胞体，细胞体再判断是不是给中枢神经汇报。 就像有时候我们看到身体有磕碰伤， 但是自己却不记得什么时候撞的， 就是磕碰的时候细胞体判断这个信息没那么重要， 就没有向中枢汇报。

McCulloch和Pitts

让我们把时间线跳转到1943年。McCulloch（下图中右边这个大胡子先生，一位神经科学家） and Pitts（下图中左边这位眼光锐利的先生，一位自学成才的逻辑学家！超厉害！）发表论文《A LOGICAL CALCULUS OF THE IDEAS IMMANENT IN NERVOUS ACTIVITY》，提出了一种高度简化的神经元模型，我们一般称其为M-P神经元模型。

图片来源 Published in Biosyst. 2007 On the legacy of W.S. McCulloch R. Moreno-Díaz, Arminda Moreno-Díaz.
他们中的其中一位就认为说，既然神经元传递信息是通过全或无定律(all-or-none law)的方式传递信息，那么就可以近似地用命题逻辑（ propositional logic）来表示：全或无，即1或0。

一种高度简化的模型

结合我们之前的知识，不论是何种神经元，皆可分成：接收区（receptive zone）、触发区（trigger zone）、传导区（conducting zone），和输出区（output zone）。

• 接收区（receptive zone）：为树突到胞体的部分（伪单极神经元为接受器的部分），会有电位的变化，为阶梯性的生电（Graded electrogenesis）。所谓阶梯性是指树突接受（接受器）不同来源的突触，如果接收的来源越多，对胞体膜电位的影响越大，反之亦然。而接受的讯息在胞体内整合。

• 触发区（trigger zone）：在胞体整合的电位，决定是否产生神经冲动的起始点。位于轴突和胞体交接的地方。也就是轴丘（axon hillock）的部分。

• 传导区（conducting zone）：为轴突的部分，当产生动作电位（action potential）时，传导区能遵守全有全无的定律（all or none）来传导神经冲动。

• 输出区（output zone）：神经冲动的目的就是要让神经末梢，突触的神经传递物质或电力释出，才能影响下一个接受的细胞（神经元、肌肉细胞或是腺体细胞），此称为突触传递。

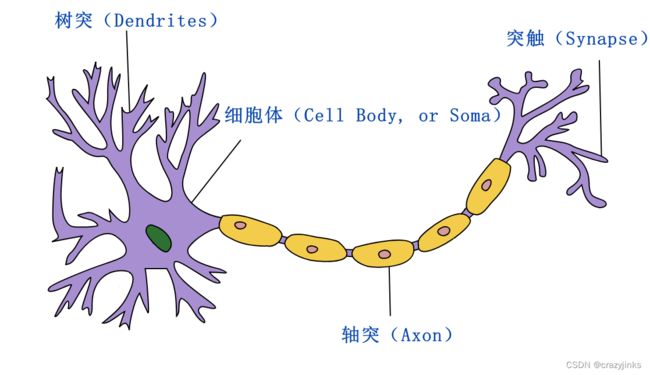
*[注:图中只标出了细胞体， 没有标出轴丘部分， 你能指出来吗?]

M-P神经元模型将其进一步抽象为如下形式：g函数将接收若干个x（0或1）求和，然后交给f函数做判断，最后输出y（0或1）

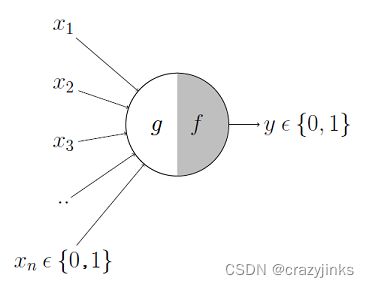
	接收区	触发区	传导区	输出区
神经元	树突（>1）+ 胞体	轴丘	轴突	突触
M-P模型	$x_1,x_2,x_3,...$ + g	f	→	y

• $x_1,x_2,x_3,...$

我们把多个树突，抽象为值为0或者1的输入$x_1,x_2,x_3,...$，根据之前的法则，要么神经元被激活， 要么完全不被激活，所以我们定义神经元未被激活则传0， 被激活则传1。

• g函数

g函数就是一个简单的求和函数，它把接收到的$x_1,x_2,x_3,...$都加起来，

• f函数
  f函数是一个简单的判断函数，判断g(x)的值是否大于阈值$\theta$，如果大于等于$\theta$，则输出1，否则输出0。
  

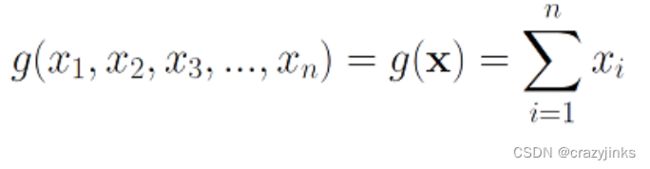
MP神经元和真值表

我们来用一个简单的例子来理解这个过程，假设我们判断一个头像是否是女性是由2个神经元决定的：$x_1$是否佩戴耳环，$x_2$是否是长发。设$\theta$ 阈值为1，那么我们判断的情况如下表示：

案例	$x_1$是否佩戴耳环	$x_2$是否是长发	g(x) 求和	$\theta$ 阈值	f(x) 做判断	y（是否是女性）
案例1	0	0	0	1	0 $<$ 1	0（男性）
案例2	1	0	1	1	1 $\ge$ 1	1（女性）
案例3	0	1	1	1	1 $\ge$ 1	1（女性）
案例4	1	1	2	1	2 $\ge$ 1	1（女性）

我们关注一下我们的输入$x_1$，$x_2$以及y，显然！进一步的，我们可以发现在阈值为1的情况下，这就是一个逻辑或的操作! 只要$x_1$，$x_2$存在一个1就会输出1！

我们把阈值提高到2，看看发生了什么

案例	$x_1$是否佩戴耳环	$x_2$是否是长发	g(x) 求和	$\theta$ 阈值	f(x) 做判断	y（是否是女性）
案例1	0	0	0	2	0 $<$ 2	0（男性）
案例2	1	0	1	2	1 $\le$ 2	0（男性）
案例3	0	1	1	2	1 $\le$ 2	0（男性）
案例4	1	1	2	2	2 $\ge$ 2	1（女性）

聪明的你已经发现了！这是一个逻辑与的操作！
当且仅当$x_1$，$x_2$都为1时，y才为1，其余情况均为0。

MP神经元的几何理解

目前我们只能接受离散的值（确切的说是布尔值），假如我们的输入x是实数呢，我们可以处理吗。(注：本小节配图来自 Mitesh M. Khapra 与 NPTEL’s Deep Learning course上提供的幻灯片)

我们再从几何的角度来理解一下这个问题，以逻辑或的操作为例。我们只有$x_1$，$x_2$这两个变量,我们以$x_1$，$x_2$建立坐标系，看看我们的M-P神经元做了些什么。我们的判断函数f判断正类的公式是$x_1+x_2\ge 1$也就是$x_2\ge -x_1+1$，这意味着$x_2=-x_1+1$这条线及以上的点被我们分类成了正类（是女性），相应的 这条线以下的被分类为了负类（男性）

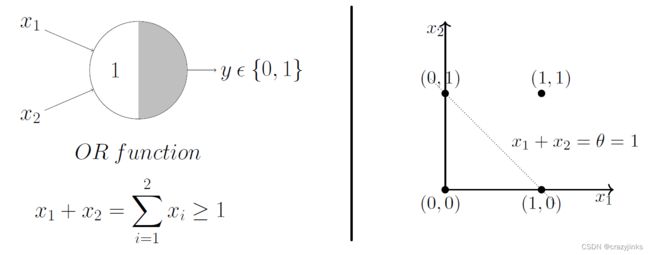
同样的，我们绘制出逻辑与的情况：

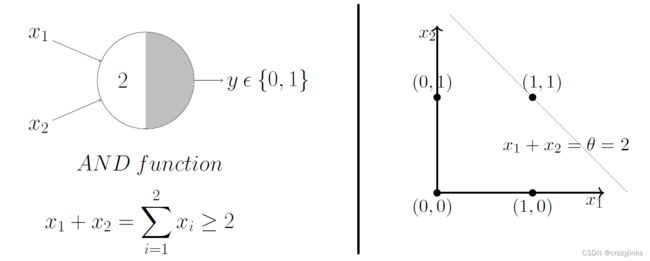
在$x_2=-x_1+1$这条线及以上区域是的样本点（$x_1$，$x_2$）均可以被我们分类为正类（是女性）

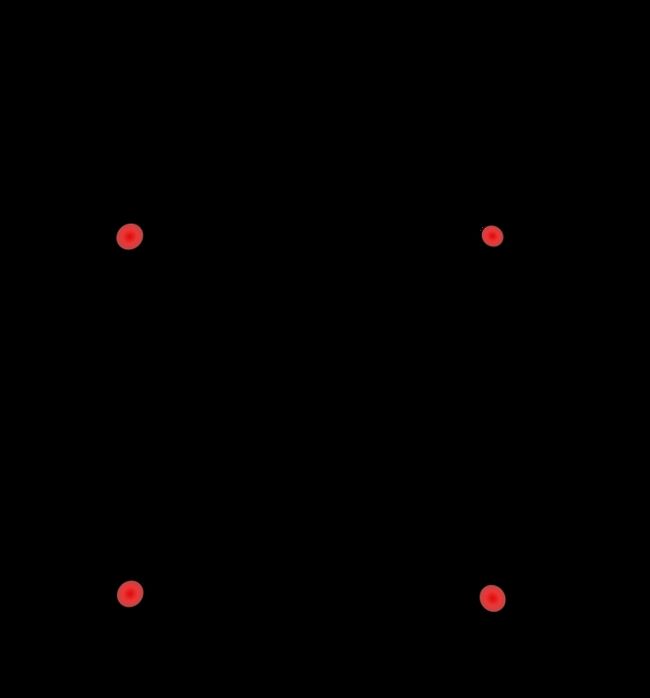
再进一步的，假如有大于2个数量的输入呢，比如我们有$x_1$，$x_2$，$x_3$三个输入，我们扩展到3维空间。我们不难发现，我们仍然可以实现上述的逻辑命题。以A or B or C为例，只需要设置阈值为1，再增加一个$x_3$作为输入就可以了。我们在一个三维的空间把这些点表记出来。以黑点表示正类，红点表示负类。我们可以看到除了（0,0,0）这个红点不在范围内，其余的黑点都被正确分类了。

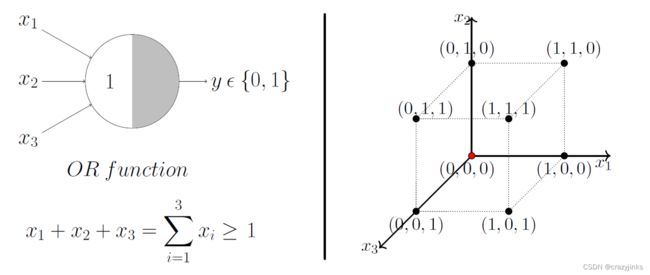
接下来我们沿着之前的思路， 看一下判断函数f的图像。我们绘制出$x_1$+ $x_2$ + $x_3=1$这个平面。

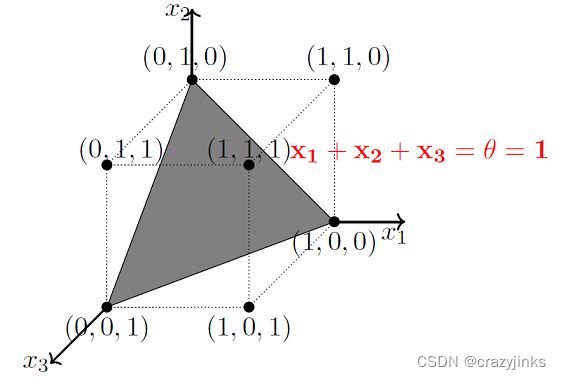
我们把这个平面想象成成一面无限的墙，它可以无限延伸。并且这面墙隔开了我们需要的正类样本点和负类样本点。尝试理解下面这句话。这个平面把我们的样本空间分成了正类和父类

好的，行文到此你已经对神经元，M-P神经元有了不错的理解。
我们还需要知道哪些问题？

1. M-P神经元能否实现所有逻辑操作？
2. 逻辑操作中，我们没有提到逻辑非（NOT），你有办法实现吗？
3. 我们已经知道了M-P神经元的输入可以扩展到实数域，如何实现？
4. M-P神经元能实现一些基本逻辑操作，但是似乎没有实现所谓的“人工智能”。

这些问题是如何被解答的，敬请期待下一篇文章《一文带你读懂感知机的前世今生(下)》

后记

1. 追求真理的同学不用深究文章开头的图像是男是女，它是由生成对抗网络（GAN）生成的人脸，关于更多信息，你可以去这个网站逛逛这个人并不存在
2. 本来我想一文写完，但是越写越长，受限于笔者水平，不得已分成两部分了。关于题目中自我标榜的一文读懂 ，现在看来多少有点哗众取众之嫌了。但是我还没有想好更好的名字，暂时这样。Have fun with it！

参考

1. https://en.wikipedia.org/wiki/Frank_Rosenblatt
2. https://news.cornell.edu/stories/2019/09/professors-perceptron-paved-way-ai-60-years-too-soon
3. https://www.nature.com/articles/d41586-019-02307-y
4. Kanal, L. N. & Randall, N. C. In Proc. 1964 19th ACM National Conf.
   42.501–42.5020 (ACM, 1964).
   5.https://www.reddit.com/r/MachineLearning/comments/ejbwvb/r_single_biological_neuron_can_compute_xor/
5. https://mind.ilstu.edu/curriculum/mcp_neurons/index.html
6. http://www.cse.iitm.ac.in/~miteshk/CS7015/Slides/Teaching/pdf/Lecture2.pdf
7. https://arxiv.org/ftp/arxiv/papers/1804/1804.01653.pdf
8. https://psychclassics.yorku.ca/Hull/Hierarchy/part1.htm
9. THE CONCEPT OF THE HABIT-FAMILY HIERARCHY AND MAZE LEARNING: Clark
   L. Hull (1934a)
10. https://www.cs.cmu.edu/~./epxing/Class/10715/reading/McCulloch.and.Pitts.pdf