卡尔曼滤波算法推导及MATLAB实现
卡尔曼滤波算法推导及MATLAB实现
最近自学了卡尔曼滤波,起初只是看了看推导过程,后来碰巧在最优控制课程上面要用它,就利用MATLAB实现了,先放个流程图,代码及推导过程后期更新。

卡尔曼滤波算法推导
这里直接给出传说中的黄金5条,具体的推导过程大家可以参考别人家的博客哦(文末有推荐)
黄金五条
- 当前时刻预测值
x ^ k − = A x ^ k − 1 + B u k − 1 \hat{x}_{k}^{-}=A{{\hat{x}}_{k-1}}+B{{u}_{k-1}} x^k−=Ax^k−1+Buk−1 - 预测值的协方差矩阵
P k − = A P k − 1 + A T + Q P_{k}^{-}=AP_{k-1}^{+}{{A}^{T}}+Q Pk−=APk−1+AT+Q - 更新卡尔曼滤波增益
K k = P k − H T ( H P k − H T + R ) − 1 {{K}_k}=P_{k}^{-}{{H}^{T}}{{\left( HP_{k}^{-}{{H}^{T}}+{{R}} \right)}^{-1}} Kk=Pk−HT(HPk−HT+R)−1 - 更新最优状态估计值
x ^ k + = x ^ k − + K k ( y k − H x ^ k − ) \hat{x}_{k}^{+}=\hat{x}_{k}^{-}+{{K}_{k}}\left( {{y}_{k}}-H\hat{x}_{k}^{-} \right) x^k+=x^k−+Kk(yk−Hx^k−) - 更新最优状态估计值的协方差矩阵
P k + = ( I − K k H ) P k − P_{k}^{+}=\left( I-{{K}_{k}}H \right)P_{k}^{-} Pk+=(I−KkH)Pk−
参数说明
| 参数 | 说明 |
|---|---|
| x ^ k − \hat{x}_{k}^{-} x^k− | 当前时刻的预测值 |
| x ^ k − 1 \hat{x}_{k-1} x^k−1 | 上一时刻的最优状态估计值 |
| P k − P_{k}^{-} Pk− | 当前时刻预测值的协方差矩阵 |
| K k K_k Kk | 卡尔曼滤波增益 |
| y k y_k yk | 当前时刻测量值 |
| x ^ k + \hat{x}_{k}^{+} x^k+ | 最优状态估计值 |
| Q , R Q,R Q,R | 过程噪声和测量噪声的协方差 |
系统模型背景
设线性化的离散系统为:
x k = A k x k − 1 + B k u k − 1 + w k − 1 {{x}_{k}}={{A}_{k}}{{x}_{k-1}}+{{B}_{k}}{{u}_{k-1}}+{{w}_{k-1}} xk=Akxk−1+Bkuk−1+wk−1 y k = H k x k + v k {{y}_{k}}={{H}_{k}}{{x}_{k}}+{{v}_{k}} yk=Hkxk+vk 其中, w k {{w}_{k}} wk是协方差为 Q k {{Q}_{k}} Qk的零均值高斯白噪声,即 w k ∼ ( 0 , Q k ) {{w}_{k}}\sim \left( 0,{{Q}_{k}} \right) wk∼(0,Qk), v k {{v}_{k}} vk是协方差为 R k {{R}_{k}} Rk的零均值高斯白噪声,即 v k ∼ ( 0 , R k ) {{v}_{k}}\sim \left( 0,{{R}_{k}} \right) vk∼(0,Rk),且 w k {{w}_{k}} wk与 v k {{v}_{k}} vk不相关。 A k {{A}_{k}} Ak为非奇异状态矩阵, B k {{B}_{k}} Bk为控制输入矩阵, H k {{H}_{k}} Hk为观测矩阵, x k {{x}_{k}} xk为 k k k时刻的系统状态, y k {{y}_{k}} yk为 k k k时刻系统的量测值, u k {{u}_{k}} uk为 k k k时刻对系统的控制量, w k {{w}_{k}} wk为系统过程噪声, v k {{v}_{k}} vk为系统量测噪声。
- 利用拉格朗日动力学方法建立了在匀速运行状态下自行车机器人系统的非线性动力学模型,在对非线性模型进线性化处理后得到了系统的线性状态空间模型,并对系统状态空间模型进行了稳定性、能控性、可观性分析。
- 研究含有系统噪声与量测噪声的自行车机器人系统的平稳控制时,对系统的线性化空间模型设计了线型二次型最优控制器(LQR)并进行了仿真,仿真结果显示LQR虽实现了系统的平稳控制,但系统响应时间长,动态特性差,稳态误差大且对扰动的抑制能力差。
- 为了优化LQR控制器,引入了卡尔曼滤波器(KF)作为系统的状态观测器,针对系统的线性化空间模型,设计了基于KF的LQR控制器,仿真结果显示引入KF状态观测器后改善了LQR控制器的动态特性,提高了系统的控制精度和鲁棒性。
MATLAB实现
下面通过MATLAB实现卡尔曼滤波
%% 加入卡尔曼滤波
% 初始化
H = [0 0 1 0]; % 观测矩阵
z = zeros(1,len); % 观测值
z(1) = H*x(:,1)+v(1); % 观测初始真实值,第一列的列向量,
x_kf = zeros(4,len);% kalman估计状态
x_kf(:,1) = x(:,1); % kalman估计状态初始化,第一列的列向量,
p0 = diag([0 0 0.1^2 0]); % 初始误差 协方差
err_p = zeros(N,4);
err_p(1,1) = p0(1,1);
err_p(1,2) = p0(2,2);
err_p(1,3) = p0(3,3);
err_p(1,4) = p0(4,4);
x_pre = zeros(4,len);
I = eye(4); % 4*4单位矩阵表明四维系统
% Kalman 滤波迭代过程
for k=2:len
x(:,k) = Ad*x(:,k-1) + Bd * u(k) + w(:,k);
z(k) = H*x(:,k) + v(k); % 量测
x_pre(:,k) = Ad*x_kf(:,k-1) + Bd*u(k); % 状态预测 -黄金(1)
p_pre = Ad*p0*Ad' + Qk; % 状态协方差预测 -黄金(2)
kg = p_pre*H'/(H*p_pre*H' + R); % 增益更新 -黄金(3)
x_kf(:,k) = x_pre(:,k) + kg*(z(k)- H*x_pre(:,k)); % 更新状态最优估计值 -黄金(4)
p0 = (I-kg*H)*p_pre; % 状态协方差更新 -黄金(5)
err_p(k,1) = p0(1,1); % 状态1误差协方差
err_p(k,2) = p0(2,2); % 状态2误差协方差
err_p(k,3) = p0(3,3); % 状态3误差协方差
err_p(k,4) = p0(4,4); % 状态4误差协方差
end
效果
完整代码
初始化
clc;
clear;
clf;
figwidth = 500;
figheight = 300;
%% 自行车参数
m_0 = 2; % 自行车前后轮的质量 2kg
m_1 = 18; % 车架的质量18kg
m_2 = 2.5; % 车把及转轴质量2.5kg
r_0 = 0.35; % 前后轮半径0.35m
h_0 = 0.9; % 车身质心到地面距离0.9m
h_1 = 1.2; % 车把手到地面距离1.2m
L = 0.5; % 车把长度0.5m
s = 0.04; % 车把转轴到前轮圆心距离0.04m
g = 9.802; % 重力加速度
%% 新参数
a = 1/(m_0*s^2 + 0.5*m_0*r_0^2 + (m_2*L^2)/3);
b = (m_0*s*r_0 + 0.5*m_2*L*h_1)/(m_0*s^2 + 0.5*m_0*r_0^2 + (m_2*L^2)/3);
c = -b;
d = 2*(2*m_0*g*r_0 + m_1*g*h_0 + m_2*g*h_1)/(3*m_0*r_0^2 + 2*m_1*h_0^2 + 2*m_2*h_1^2);
e = -(m_0*s*r_0 + 0.5*m_2*L*h_1)/(3*m_0*r_0^2 + 2*m_1*h_0^2 + 2*m_2*h_1^2);
% 线性化后的常数矩阵
A = [0 1 0 0;0 0 c*d/(1-c*e) 0;0 0 0 1;0 0 d/(1-c*e) 0];
B = [0 a/(1-c*e) 0 e*a/(1-c*e)]';
C =[0 0 1 0];
D = 0;
CONT=ctrb(A,B);% 可控矩阵
RankC = rank(CONT);
OBSER = obsv(A,C); % 可观矩阵
RankO = rank(OBSER);
Q = [1 0 0 0;0 1 0 0;0 0 1 0;0 0 0 1];
R = [1];
N = 0;
[K,S,e] = lqr(A,B,Q,R); % 连续
无噪声响应
%% 加入lQR控制器后的系统矩阵
Ac = (A-B*K);
Bc = B;
Cc = C;
Dc = D;
ts = 0.1; % 采样时间
t = 0:ts:20;
len = length(t);
[Ad,Bd,Cd,Dd]=c2dm(Ac,Bc,Cc,Dc,ts,'z'); % 离散化' 加入LQR后
%% 没加噪声的响应
u = 1*ones(size(t));
x_0 = zeros(4,len);
y_0 = zeros(1,len);
x_0(:,1) = [0 0 0.1 0]'; % 状态初始化
y_0(:,1) = Cd*x_0(:,1);
for k=2:len
x_0(:,k) = Ad*x_0(:,k-1) + Bd*u(k);
y_0(k) = Cd*x_0(:,k);
end
卡尔曼滤波
%% 加入噪声的响应
Qc = 5*10e-6;
Qk = diag([Qc Qc Qc Qc]);
Rc = 0.001;
Rk = diag([Rc Rc]);
w = normrnd(0,Qc,4,len); % 过程噪声 产生均值为a、方差为b大小为cXd的随机矩阵
v = normrnd(0,Rc,1,len); % 量测噪声
x = zeros(4,len); % 物体真实状态
y = zeros(1,len); % 输出
x(:,1) = [0 0 0.1 0]'; % 状态初始化
y(:,1) = Cc*x(:,1);
% 加入卡尔曼滤波
% 初始化
H = [0 0 1 0]; % 观测矩阵
z = zeros(1,len); % 观测值
z(1) = H*x(:,1)+v(1); % 观测初始真实值,第一列的列向量,
x_kf = zeros(4,len);% kalman估计状态
x_kf(:,1) = x(:,1); % kalman估计状态初始化,第一列的列向量,
p0 = diag([0 0 0.1^2 0]); % 初始误差 协方差
err_p = zeros(N,4);
err_p(1,1) = p0(1,1);
err_p(1,2) = p0(2,2);
err_p(1,3) = p0(3,3);
err_p(1,4) = p0(4,4);
x_pre = zeros(4,len);
I = eye(4); % 4*4单位矩阵表明四维系统
% Kalman 滤波迭代过程
for k=2:len
x(:,k) = Ad*x(:,k-1) + Bd * u(k) + w(:,k);
z(k) = H*x(:,k) + v(k); % 量测
x_pre(:,k) = Ad*x_kf(:,k-1) + Bd*u(k); % 状态预测 黄金(1)
p_pre = Ad*p0*Ad' + Qk; % 状态协方差预测 黄金(2)
kg = p_pre*H'/(H*p_pre*H' + R); % 增益更新 黄金(3)
x_kf(:,k) = x_pre(:,k) + kg*(z(k)- H*x_pre(:,k)); % 更新状态最优估计值 黄金(4)
p0 = (I-kg*H)*p_pre; % 状态协方差更新 黄金(5)
err_p(k,1) = p0(1,1); % 状态1误差均方值
err_p(k,2) = p0(2,2); % 状态2误差均方值
err_p(k,3) = p0(3,3); % 状态1误差均方值
err_p(k,4) = p0(4,4); % 状态2误差均方值
end
绘图
%% ---画图 协方差
figure(1)
plot(t,err_p(:,3),'b','LineWidth',1.5)
title('车身倾角的误差协方差变化曲线','FontWeight','bold')
xlabel('time/s','FontWeight','bold','FontSize',10,'Interpreter','latex')
ylabel('$$P$$','FontWeight','bold','FontSize',14,'Interpreter','latex')
savefig(gcf,figwidth,figheight,'fig\P.jpg')
%% 绘制车把倾角 在有噪声跟没噪声下的阶跃响应
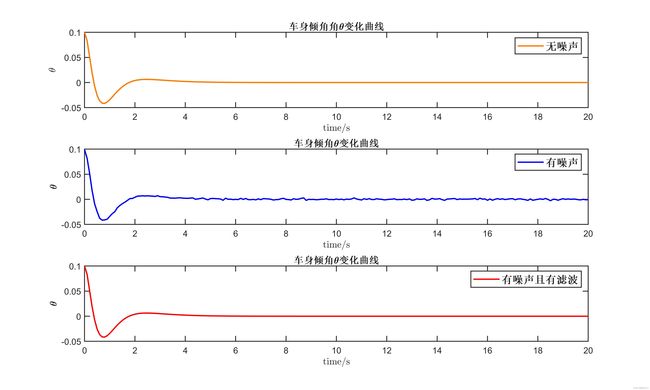
figure(2)
subplot(3,1,1)
plot(t,y_0,'color',[0.99, 0.49, 0.00],'LineWidth', 1.5)
title('车身倾角角\theta变化曲线','FontWeight','bold')
xlabel('time/s','FontWeight','bold','FontSize',10,'Interpreter','latex')
ylabel('$$\theta$$','FontWeight','bold','FontSize',14,'Interpreter','latex')
legend('无噪声','FontSize',12,'FontWeight','bold')
set(gca, 'FontSize',10) % 设置坐标轴字体是 8
set(gca, 'Linewidth',1) % 设置坐标轴字体是 8
%%
subplot(3,1,2)
plot(t,z,'color','b','LineWidth', 1.5)
title('车身倾角\theta变化曲线','FontWeight','bold')
xlabel('time/s','FontWeight','bold','FontSize',10,'Interpreter','latex')
ylabel('\theta','FontWeight','bold','FontSize',14)
legend('有噪声','FontSize',12,'FontWeight','bold')
set(gca, 'FontSize',10) % 设置坐标轴字体是 8
set(gca, 'Linewidth',1) % 设置坐标轴字体是 8
%% 绘制车身滚角 在有噪声跟没噪声下的阶跃响应
subplot(3,1,3)
plot(t,x_kf(3,:),'r','LineWidth', 1.5)
title('车身倾角\theta变化曲线','FontWeight','bold')
xlabel('time/s','FontWeight','bold','FontSize',10,'Interpreter','latex')
ylabel('\theta','FontWeight','bold','FontSize',14)
legend('有噪声且有滤波','FontSize',12,'FontWeight','bold')
set(gca, 'FontSize',10) % 设置坐标轴字体是 8
set(gca, 'Linewidth',1) % 设置坐标轴字体是 8
set(gcf,'color','white');
savefig(gcf,1000,600,'fig\CSDN_1.jpg')
%%
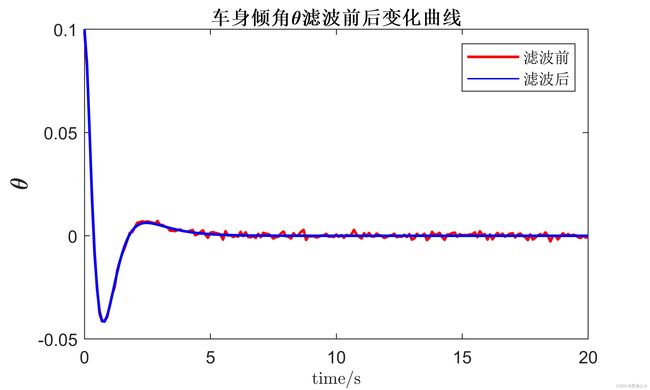
filepath = 'fig\CSDN_2.jpg'
figure(3)
title('滤波前后的比较')
plot(t,z,'r','LineWidth',1.5)
hold on
plot(t,x_kf(3,:),'b','LineWidth',1.5)
title('车身倾角\theta滤波前后变化曲线','FontWeight','bold')
xlabel('time/s','FontWeight','bold','FontSize',10,'Interpreter','latex')
ylabel('\theta','FontWeight','bold','FontSize',14)
legend('滤波前','滤波后')
savefig(gcf,figwidth,figheight,filepath)
代码中的savefig函数链接
参考
卡尔曼滤波详细推导
知乎