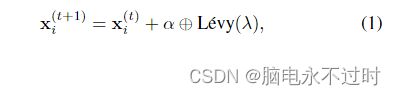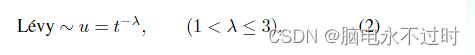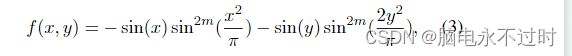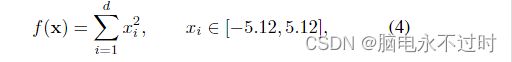通过L-evy飞行进行布谷鸟搜索

英文：Cuckoo Search via L ́ evy Flights

在本文中，我们打算制定一种新的元启发式算法，称为布谷鸟搜索(CS)，用于解决优化问题。这个算法是基于一些布谷鸟物种的强制性的幼虫寄生行为与一些鸟类和果蝇的L-evy飞行行为相结合。我们针对测试函数验证了所提出的算法，然后将其性能与遗传算法和粒子群优化的性能进行比较。最后，我们讨论了这些结果的含义和对进一步研究的建议。

1. 引言

越来越多受自然启发的现代元启发式算法正在出现，并且越来越流行。例如，粒子群优化（PSO）受到鱼和鸟群智能的启发，而萤火虫算法受到热带萤火虫闪烁模式的启发[2]，[3]，[6]，[21]，[22]。这些自然启发的元启发式算法已用于广泛的优化问题，包括NP难问题，如旅行推销员问题[2]、[3]、[6]、[8]、[10]、[21]。

几乎所有现代元启发式的力量都来自于这样一个事实，即它们模仿自然界的最佳特征，特别是数百万年来由自然选择进化而来的生物系统。两个重要特征是适者选择和适应环境。从数字上讲，这些可以转化为现代元启发式的两个关键特征：强化和多样化[3]。强化旨在围绕当前最佳解决方案进行搜索，并选择最佳候选方案或解决方案，而多样化确保算法能够有效地探索搜索空间。

本文旨在制定一种新的算法，称为杜鹃搜索（CS），该算法基于有趣的繁殖行为，如某些杜鹃物种的卵寄生。我们将首先介绍杜鹃的繁殖行为以及一些鸟类和果蝇的飞行特征，然后制定新的CS，然后实施。最后，我们将把提出的搜索策略与其他流行的优化算法进行比较，并讨论我们的发现及其对各种优化问题的影响。

二、杜鹃鸟和levy飞行

A、杜鹃鸟行为

杜鹃是一种令人着迷的鸟类，不仅因为它们能发出美妙的声音，还因为它们积极的繁殖策略。一些物种，如阿尼杜鹃和吉拉杜鹃，在公共巢穴产卵，尽管它们可能会移除其他物种的卵，以增加自己卵的孵化概率[12]。相当多的物种通过在其他寄主鸟类（通常是其他物种）的巢穴中产卵来进行专性的卵寄生。有三种基本类型的卵寄生：种内卵寄生、合作繁殖和巢接管。一些寄主鸟类可以和入侵的杜鹃发生直接冲突。如果一只寄主鸟发现这些蛋不是自己的，它们要么扔掉这些外来蛋，要么干脆放弃自己的巢穴，在别处建一个新的巢穴。一些杜鹃物种，如新世界的寄生杜鹃，其进化方式使得雌性寄生杜鹃通常非常擅长模仿少数选定宿主物种的卵的颜色和图案[12]。这降低了它们的卵被遗弃的概率，从而提高了它们的繁殖能力。

此外，一些物种产卵的时间也很惊人。寄生杜鹃经常选择寄主鸟刚刚产卵的巢穴。一般来说，杜鹃鸟卵孵化的时间略早于寄主卵。一旦第一只杜鹃雏鸟孵化出来，它会采取的第一个本能行动是通过盲目地将寄主蛋推出巢穴来驱逐寄主蛋，这会增加杜鹃幼鸟在寄主鸟提供的食物中的份额。研究还表明，其也可以模仿寄主鸟的叫声，以获得更多的喂食机会。

B、levy飞行

另一方面，各种研究表明，许多动物和昆虫的飞行行为证明了Láevy飞行的典型特征[4]，[15]，[13]，[14]。Reynolds和Frye最近的一项研究表明，果蝇或果蝇利用一系列直线飞行路径探索它们的景观，这些直线飞行路径被突然的90度转弯打断，从而形成了Láevy飞行式的间歇无尺度搜索模式。对人类行为的研究，如Ju/‘hoansi狩猎采集者觅食模式，也显示了Láevy飞行的典型特征。即使是光也可能与Láevy航班有关。随后，这种行为被应用于优化和优化搜索，初步结果显示其有前途的能力。

三、布谷鸟算法

为了简单描述我们的新杜鹃搜索，我们现在使用以下三个理想化规则：1）每只杜鹃每次产一个蛋，并将其蛋倒在随机选择的巢中；2） 最好的巢和高质量的蛋将传到下一代；3） 可用寄主巢穴的数量是固定的，杜鹃所产的蛋被寄主鸟发现的概率为Pa∈[0, 1]. 在这种情况下，寄主鸟可以扔掉蛋，也可以抛弃巢穴，建立一个全新的巢穴。为了简单起见，最后一个假设可以近似为n个巢穴中的Pa部分被新的巢穴替换（使用新的随机解）。

对于最大化问题，解的质量或适合度可以简单地与目标函数的值成比例。其他形式的适应度可以以与遗传算法中的适应度函数类似的方式定义。为了简单起见，我们可以使用以下简单的表示，即巢中的每个蛋代表一个解决方案，而布谷鸟蛋代表一个新的解决方案，目的是使用新的、可能更好的解决方案（布谷鸟蛋）来替换巢中不太好的解决方案。当然，该算法可以扩展到更复杂的情况，即每个巢都有多个代表一组解的蛋。对于目前的工作，我们将使用最简单的方法，每个巢只有一个蛋。

基于这三个规则，布谷鸟搜索(CS)的基本步骤可以概括为伪代码

---

 开始：

     目标函数 f(x)

      生成的初始种群：n个宿主巢穴x i（i=1，2，…，n）

      (循环) 当（t<最大迭代次数或者终止条件）

               通过levy飞行随机获得一只杜鹃

                计算其适应度Fi

                if( Fi>Fj)

                       用新的解决方案替换j

                 一小部分（pa）更糟糕的巢穴被废弃，新的巢穴建立起来；

                保持最佳解决方案（或以优质解决方案筑巢）；

                 对解决方案进行排名并找出当前

处理结果和可视化

---

当生成新的解决方案x (t+1)，例如，一个布谷鸟i， 进行一次Levy飞行。

 其中α>0是步长，其应与兴趣问题的尺度相关。在大多数情况下，我们可以使用α=1。上述方程本质上是随机行走的随机方程。一般来说，随机游走是马尔可夫链，其下一状态/位置仅取决于当前位置（上述等式中的第一项）和转移概率（第二项）。符号⊕表示入口乘法。这一符号与PSO中使用的符号相似，但在这里，通过Levy飞行的随机漫游在探索搜索空间方面更有效，因为从长远来看，它的步长要长得多。

Levy飞行本质上提供了一个随机行走，而随机步长则从Levy分布中抽取

 其具有无穷的方差和无穷的平均值。在这里，这些步骤基本上形成了一个随机行走过程，其具有带有重尾的幂律步长分布。一些新的解决方案应该由Levy生成，绕着迄今为止获得的最佳解决方案走一走，这将加快本地搜索的速度。然而，新解的很大一部分应通过远区域随机化生成，其位置应与当前最佳解相距足够远，这将确保系统不会陷入局部最优。

从快速观察来看，CS和爬山结合一些大规模随机化似乎有一些相似之处。但有一些显著的差异。首先，CS是一种基于种群的算法，类似于GA和PSO，但它使用了某种精英主义的选择，类似于和声搜索（harmony search）中使用的算法。其次，随机化更有效，因为步长是重尾的，任何大步都是可能的。第三，要调整的参数数量少于GA和PSo，因此它可能更通用，以适应更广泛的优化问题。此外，每个巢穴可以表示一组解，因此CS可以扩展到元种群算法的类型。

四、实验

A、 验证和参数研究

在实现之后，我们必须使用具有分析或已知解决方案的测试函数来验证算法。例如，我们使用的许多测试函数之一是二元Michaelwicz函数：

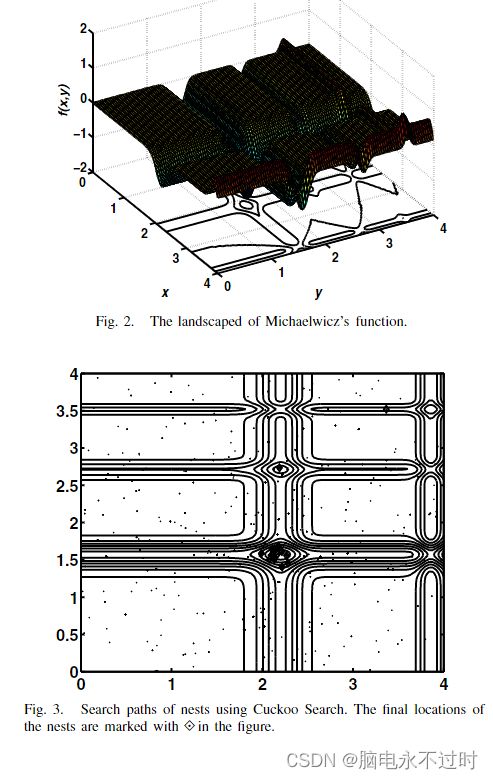
 其中m=0，(x, y) ∈[0, 5]，此函数具有全局最小值f∗ ≈− 1.8013，当（x，y）=（2.20319，1.57049）。使用Cuckoo Search可以很容易地找到这个全局最优值，结果如图3所示，图中巢穴的最终位置也用·标记。这里我们使用了n=15个巢穴，α=1和Pa=0.25。在我们的大多数模拟中，我们使用n=15到50。

从图中，我们可以看到，随着最优值的接近，大多数巢穴向全局最优值聚集。我们还注意到，在多模态函数的情况下，巢穴也分布在不同的（局部）最优点。这意味着，如果巢穴的数量远高于局部优化的数量，CS可以同时找到所有优化。当处理多模态和多目标优化问题时，这一优势可能会变得更加重要。

我们还尝试改变宿主巢穴的数量（或种群大小n）和概率pa。我们使用了n=5、10、15、20、50、100、150、250、500和pa=0、0.01、0.05、0.1、0.15、0.2、0.25、0.4、0.5。从我们的模拟中，我们发现n=15和pa=0.25足以解决大多数优化问题。结果和分析还表明，收敛速度在某种程度上对所使用的参数不敏感。这意味着对于任何给定的问题都不需要进行微调。因此，我们将在其余的模拟中使用固定的n=15和p a=0.25，特别是在下一篇文章中给出的比较研究中。

B、测试功能

文献[5]、[17]、[16]中有许多基准测试函数，它们被设计用于测试优化算法的性能。任何新的优化算法也应该针对这些基准函数进行验证和测试。在我们的模拟中，我们使用了以下测试函数。

De Jong的第一个函数本质上是一个球面函数

 C、CS与PSO和GA的比较

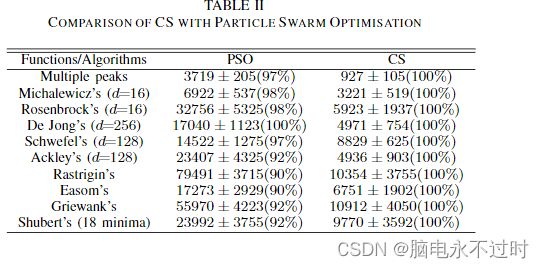
最近的研究表明，PSO算法在许多优化问题上可以优于遗传算法（GA）[8]和其他传统算法。这在一定程度上可以归因于当前最佳估计的广播能力，这可能会更好更快地收敛到最佳状态。Shilane等人详细讨论了评估进化算法统计性能的一般框架。

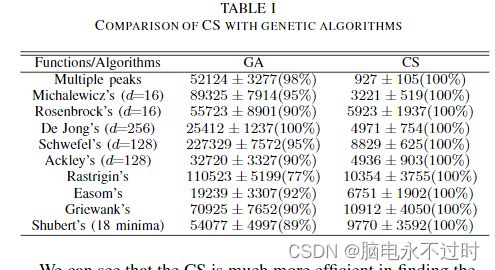
现在我们将比较杜鹃搜索与PSO和遗传算法的各种标准测试功能。在使用Matlab实现这些算法之后，我们进行了广泛的模拟，每个算法至少运行了100次，以便进行有意义的统计分析。当函数值的变化小于给定公差时，算法停止≤ 10−5.结果汇总于下表（见表1和表2），其中达到了全局最优值。这些数字的格式为：平均求值次数（成功率），因此927±105（100%）意味着函数求值的平均次数（平均值）为927，标准偏差为105。找到该算法的全局最优值的成功率为100%。

 可以看出，CS在以更高的成功率找到全局最优值方面效率更高。在现代个人计算机上，每个功能评估几乎都是即时的。例如，在3GHz桌面上进行10000次评估的计算时间约为5秒。

对于所有测试功能，CS都优于GA和PSO。主要原因有两方面：随机化和强化的良好平衡，以及较少的控制参数。对于任何元启发式算法，密集的局部搜索策略和对整个搜索空间的有效探索之间的良好平衡通常会导致更高效的算法。另一方面，该算法中只有两个参数，即种群大小n和pa。一旦n被固定，pa基本上控制了精英化以及随机化和局部搜索的平衡。很少有参数使算法不那么复杂，因此可能更通用。这些观察值得在今后的工作中进行更系统的研究和进一步的阐述。

五、 结论

在本文中，我们基于一些杜鹃物种的繁殖策略，结合Láevy飞行，制定了一种新的元启发式杜鹃搜索。该算法已经过验证，并与遗传算法和粒子群优化等其他算法进行了比较。仿真和比较表明，对于多模态目标函数，CS算法优于现有算法。这部分是由于CS中需要微调的参数比PSO和遗传算法中要少。事实上，除了种群大小n，基本上只有一个参数pa。此外，我们的模拟还表明收敛速度对参数pa不敏感。这也意味着我们不必针对特定问题微调这些参数。随后，与其他元启发式算法相比，CS对于许多优化问题更为通用和鲁棒。

这种潜在强大的优化策略可以很容易地扩展到研究具有各种约束的多目标优化应用，甚至是NP难问题。进一步的研究可以集中于灵敏度和参数研究，以及它们与算法收敛速度的可能关系。与其他流行算法（如PSO）的混合也将是潜在的成果