机器学习入门（九）：非监督学习：5种聚类算法+2种评估模型

机器学习入门专栏其他章节：

机器学习入门（一）线性回归

机器学习入门（二）KNN

机器学习入门（三）朴素贝叶斯

机器学习入门（四）决策树

机器学习入门（五）集成学习

机器学习入门（六）支持向量机

机器学习入门（七）多项式回归

机器学习入门（八）主成分分析

聚类算法(Clustering Algorithms)常用于进行非监督学习（unsupervised learning)，即它处理的是没有事先标记分类的数据。一共介绍五种常见聚类算法:
K-means
Hierarchical
GMM
DBSCAN(基于密度的聚类算法）
基于网格Grid的聚类算法

聚类算法

距离公式

在了解聚类算法如何实现之前，需要先了解几种常见的距离计算公式，因为聚类算法会通过距离判断两个点是否属于同一类。

欧式距离：假设有两个点$(x_1,y_1),(x_2,y_2)$则距离d为：

$$d=\sqrt{(x_1-x_2{)}^2+(y_1-y_2{)}^2}$$
扩展到更加一般的情况则是：
$$d=({\Sigma }_{i=1}^n(x_1^{(i)}-x_2^{(i)}{)}^2{)}^{1/2}$$

曼哈顿距离:
对于两个点则是：
$$d=|x_1-x_2|+|y_1-y_2|$$

其他比较出名的还有Minkowski明氏距离, chebyshev切比雪夫距离，cosine余弦距离等，再次不过多展开。

K-means算法

算法过程如下：
（1）初始化聚类点centroid
（2）计算距离，将每个点分配到最近的聚类
（3）取每个聚类的平均值，获得新的聚类点centroid
（4）重复（2），（3）直到不再变化
用数学公式表达就是SSE(sum of squared error) 达到最小的时候:
$$SSE={\Sigma }_{j=1}^k{\Sigma }_{x\in C_j}d(x,m_j{)}^2$$第一个求和是所有的聚类，第二个求和是每个聚类的中心点到聚类中所有点的距离平方和。

直接调用实现

基于sklearn，可以直接调用现有的kmeans算法。
首先导入包:

import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets.samples_generator import make_blobs
X, y_true = make_blobs(n_samples=300, centers=4,
                       cluster_std=0.60, random_state=0)
from sklearn.cluster import KMeans,MiniBatchKMeans
#训练模型
k=4
kmeans = KMeans(n_clusters=k)
minimeans=MiniBatchKMeans(n_clusters=k)
kmeans.fit(X)
y_kmeans = kmeans.predict(X)
y_kmeans2 = minimeans.fit_predict(X)
#绘制图像
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis')
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='black', s=200, alpha=0.5);
plt.show()
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans2, s=50, cmap='viridis')
centers2 = minimeans.cluster_centers_
plt.scatter(centers2[:, 0], centers2[:, 1], c='black', s=200, alpha=0.5);
plt.show()

查看结果：
kmeans模型的训练结果

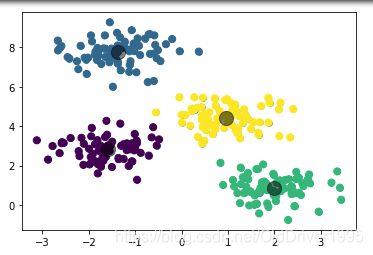
MiniBatchMeans的训练结果：

MiniBatchKmeans是另一种优化实现，它比Kmeans更快，但结果可能不同

基于EM的实现

EM算法分为E和M两个步骤，具体步骤和之前类似：
（1）随机初始化聚类中心点
（2）计算距离，分配点
（3）重新获得中心点
（4）重复（2），（3）直到停止

代码实现

from sklearn.metrics import pairwise_distances_argmin
def find_clusters(X, n_clusters, rseed=2):

	rng = np.random.RandomState(rseed)
	#随机初始化
	i = rng.permutation(X.shape[0])[:n_clusters]
	centers = X[i]
	while True:
		#计算距离
		labels = pairwise_distances_argmin(X, centers, metric='euclidean')
		#重新计算中心点
		new_centers = np.array([X[labels == i].mean(0)
                                for i in range(n_clusters)])
                #判断是否停止
                if np.all(centers == new_centers):
                	break
                centers = new_centers
        return centers, labels
#获得图像
centers, labels = find_clusters(X, 4)
plt.scatter(X[:, 0], X[:, 1], c=labels,
            s=50, cmap='viridis');
plt.scatter(centers[:,0],centers[:,1],c='red',s=100,alpha=0.5)
plt.show()

结果跟上面的图类似，不再展示。

局限性

kmeans 算法对于不同密度，不同大小的，或者非球形形状的数据，有一定限制

from sklearn.datasets import make_moons
X, y = make_moons(200, noise=.05, random_state=0)
labels = KMeans(2, random_state=0).fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=labels,s=50, cmap='viridis')
plt.show()

传统的kmeans表现非常不好：

这个时候有一种优化方式，类似SVM算法中的核函数，具体过程不展开，直接调用现有算法实现：

from sklearn.cluster import SpectralClustering
model = SpectralClustering(n_clusters=2, affinity='nearest_neighbors',assign_labels='kmeans')
labels = model.fit_predict(X)
plt.scatter(X[:, 0], X[:, 1],c=labels,s=50,cmap='viridis')
plt.show()

kmeans算法还有个缺点是，需要提前设置好k，即聚类cluster的个数，这种设置在某种程度上不太像非监督学习，接下来的有些算法则可以避免这个问题。

Hierarchical Clustering算法

Hierarchical 层次聚类这种算法不需要预设K值，它通过将距离较近的点或者聚类融入到一起，最后会实现一种树形结构的等级关系图，这也是hierarchical（层级，等级制度）这个名字的由来。

这个算法分为自顶向下（top down, Divisive)和自下而上(bottom up, Agglomerative)两种生成方式
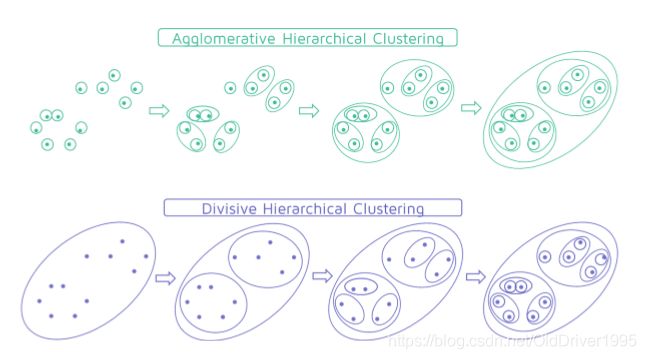由于涉及到计算聚类之间的距离，这里参考的不是距离的计算方式，而是考虑聚类的哪一个点用来计算距离（在kmeans中是每个点和平均值点计算距离），一共三种方式：

single-link: 距离最短的点
complete-link：距离最大的点
average-link：两个类中每个点的距离的平均值

代码实现

导入包

import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets.samples_generator import make_blobs
X
from scipy.cluster.hierarchy import  dendrogram, linkage

用现有的函数可以很快生成

X, y_true = make_blobs(n_samples=20, centers=3,cluster_std=0.60, random_state=0)
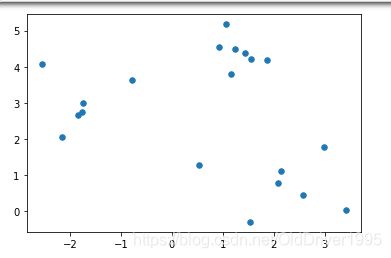
plt.scatter(X[:, 0], X[:, 1], s=30)
plt.show()
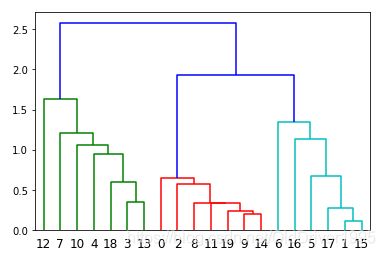
link_matrix=linkage(X,'single')
dendrogram(link_matrix)
plt.show()

局限性

对噪音敏感
对非球形数据处理效果不佳

GMM（Gaussian Mixture Model高斯混合模型）

先看这么一个例子，将数据进行一定的处理，使得它们非常紧密：

rng = np.random.RandomState(13)
X, y_true = make_blobs(n_samples=400, centers=4,cluster_std=0.60, random_state=0)
X = X[:, ::-1]
X2 = np.dot(X, rng.randn(2, 2))
kmeans=KMeans(4, random_state=0)
labels = kmeans.fit_predict(X2)
plt.scatter(X2[:, 0], X2[:, 1], c=labels,s=50, cmap='viridis')
plt.show()

因为kmeans是取均值求中心点，但有的时候均值并不是最好的方式，如上图这种形式就不适合kmeans，使用高斯混合模型可以避免这种情况，在某种程度上，kmeans是GMM的一种特例，他们本身都是基于EM算法的思想实现的。

代码实现

首先有一个画椭圆范围的函数，如果看不懂不用深入，直接调用

from matplotlib.patches import Ellipse
def draw_ellipse(position, covariance, ax=None, **kwargs):
    """Draw an ellipse with a given position and covariance"""
    ax = ax or plt.gca()
    
    # Convert covariance to principal axes
    if covariance.shape == (2, 2):
        U, s, Vt = np.linalg.svd(covariance)
        angle = np.degrees(np.arctan2(U[1, 0], U[0, 0]))
        width, height = 2 * np.sqrt(s)
    else:
        angle = 0
        width, height = 2 * np.sqrt(covariance)
    
    # Draw the Ellipse
    for nsig in range(1, 4):
        ax.add_patch(Ellipse(position, nsig * width, nsig * height,angle, **kwargs))
        

然后是gmm的实现：

from sklearn.mixture import GaussianMixture as GMM
gmm = GMM(n_components=4, random_state=42, max_iter=1, warm_start=True)
labels2 = gmm.fit_predict(X2)
plt.scatter(X2[:, 0], X2[:, 1], c=labels2, s=40, cmap='viridis', zorder=2)
w_factor = 0.2 / gmm.weights_.max()
for pos, covar, w in zip(gmm.means_, gmm.covariances_, gmm.weights_):
    draw_ellipse(pos, covar, alpha=w * w_factor)

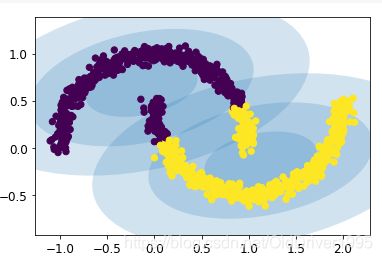
局限性

在这个例子中，gmm发挥良好，但是在他和kmeans一样，对于非球形数据的表现依旧不是很好，比如之前的月牙形数据，他就不能很好发挥。对于形状比较诡异，密度不均的数据，就要用到后面的算法。

DBSCAN

DBSCAN的全称是（Density Based Spatial Clustering of Applications with Noise) 从名字上来看就得知它是基于密度的，并且可以应付噪音。

算法详解

DBSCAN首先要直到两个参数：
Epsilon $ϵ$, 它决定了一个点的“势力范围”，如果某个点的邻居想要和他属于同一类，则需要距离小于这个半径

MinPts： Minimum Points，限定了最少在规定的$ϵ$ 半径内，有多少个点

看到这里不是很懂，没有关系，继续看规定了三种点的类型，分别是：

core point 核心点：一个点在规定半径$ϵ$ 内，含有至少MinPts这么多个点，那这个点即为核心点

border point 边界点： 在核心点旁边，但半径内个数不足MinPts

Noise/Outlier point 噪音/外部点：既不是核心点也不是边界点。

三种点如下图：

关于半径$ϵ$的选择，如果太大，则所有点都是core点，反之，所有点都是noise了。

三种点之间的关系：

图中，所有红点都是core point，黄点是border point，蓝点是noise

Directly Density Reachable：
距离小于$ϵ$，并且直接和core point相连。比如，所有红点和它旁边紧挨着的红点都是directly reachable，C点和它旁边的core红点也属于这样的关系。但需要注意的是reachable关系都不是对称的，只能说core point reaches border point（图中指向黄点的箭头是有方向的，而红点之间的箭头是双向的），而一个边界点是不能被reach的(维基解释：Reachability is not a symmetric relation: by definition, only core points can reach non-core points. The opposite is not true, so a non-core point may be reachable, but nothing can be reached from it）

Density Reachable：
两个点，没有直接相连，但他们中间存在着至少一个点，每个点相互之前都是directly reachable的，有点类似于传递。比如图中左边的红点和右边的红点就是这种关系。同样地，B点和A点也是这样地关系，但BC不是,因为reachable关系必须满足其中某一方是core point。如果一个点是和一个cluster中的某个点是reachable关系，则这个点也属于这个cluster，所以BC也属于这个cluster。

Density Connected:
存在两个点p,q，如果有另一个点o和他们依次都是reachable的，那么p和q就是connected状态，这种关系适用于B和C，他不要求其中某一方是core。更广泛的情况，一个聚类中，任意两个点都是connected的。

当清楚了这几种关系后，DBSCAN算法的执行过程就可以理解了。在遍历点的时候，对与其中一个点，它会找到所有和这个点density-connected的点，把他们全部都放到同一个cluster中，直到没有点和它connected，进而前往下一个没有遍历过的点（所有connected的点都属于遍历过的）。

代码实现

生成数据

from sklearn.datasets import make_moons
X, y = make_moons(n_samples=1000, noise=0.05, random_state=42)
plt.scatter(X[:,0], X[:,1], s=10)

当使用gmm时，会形成如下的结果：

使用DBSCAN实现：

from sklearn.cluster import DBSCAN
dbscan = DBSCAN(eps=0.05, min_samples=5)
dbscan.fit(X)
###查看一共生成了多少个cluster
np.unique(dbscan.labels_)

生成如下结果, 一共7个类+noise：

array([-1,  0,  1,  2,  3,  4,  5,  6])

如果只想看最简单的图像，可以直接这样：

plt.scatter(X[:,0], X[:,1],c=dbscan.labels_, s=40, cmap='viridis')

如果想看的更加仔细，可以像下面这样设置，把三种不同的点分别取出来：

首先弄一个全False数组，维度跟dbscan.labels一样。

由于dbscan自动记录core point，所以直接用core_sample_indices把对应的点先设成True

然后noise是所有labels==-1的点，这个方式同样可以获得一个True/False数组。

然后对于border point，用~这个操作取反。

具体代码如下：

#retrieve the index of 3 kinds of points
core_index=np.zeros_like(dbscan.labels_, dtype=bool) #创建一个跟labels长度一样，但全为T/F的数组
core_index[dbscan.core_sample_indices_]=True #dbscan自动已经存储了哪些是core，所以直接将对应index的设成True
noise_index=dbscan.labels_==-1
border_index=~(core_index | noise_index) #neither core, nor noise

#get correspond point
core=X[core_index]
border=X[border_index]
noise=X[noise_index]

#plot core point
plt.scatter(core[:,0], core[:,1],c=dbscan.labels_[core_index], s=40, cmap='viridis')
#plot border point
plt.scatter(border[:,0], border[:,1],c='grey', marker='^')
#plot noise
plt.plot(noise[:,0],noise[:,1],'rx')

结果：

灰色是border点，红x是噪音，剩余的是core点。注意所有的border其实也属于它附近的cluster，如果直接scatter所有的点，那他们border会跟对应的core是一种颜色。

可以发现，一共分出来7个cluster，效果不是很好

于epsilon设置的有点小，导致生成了很多类，现在适当修改一下参数，进行对比，将eps设置为0.08，获得如下图象，训练效果有一定提升。

eps设置为0.2：

可以看出，不同的参数，对结果的影响非常明显。所以参数的选择也应该仔细考虑

基于网格的聚类算法

这里将用到clique算法，具体实现原理暂不讲解。

代码实现

这里需要用到pyclustering包

!pip install pyclustering
from pyclustering.cluster.clique import clique,clique_visualizer
intervals = 30 #决定了网格的个数，interval越大，网格越多
threshold = 0 #每个点都会被考虑，网格中的点小于这个数值，该网格会被当成outlier
#数据还是之前的半月形数据X
clique_instance = clique(X, intervals, threshold)

clique_instance.process()
clusters = clique_instance.get_clusters()
noise = clique_instance.get_noise()
cells = clique_instance.get_cells()
clique_visualizer.show_grid(cells, X)   #show formed grid
clique_visualizer.show_clusters(X, clusters, noise)

可以得到如下结果：

注意第二个图中有个小绿点，所以实际上有三个cluster

将intervals设成20，threshold设成4，由于阈值提高，很多网格不满足要求，会产生很多cluster

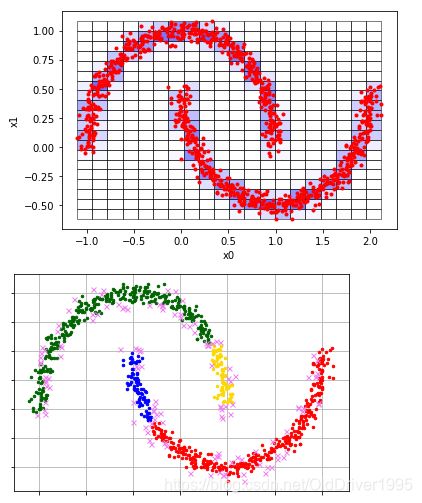
其中粉色点是噪音

局限性

不好处理高度不规则数据
受限于提前设置好的网格数量，边界，还有密度阈值（threshold）
不好处理高维数据。

模型评估evaluation

由于是非监督学习，没有y标签值判断是否分类正确，所以需要其他的方式来判断其算法模型的优劣。evaluation的方式有很多种，实际算法中并没有最，具体模型具体对待。评估方式主要说以下两种。

这里并不进行严格的数学证明，只是提供方式和思路。

elbow method

通过该算法可以选择最优的K数量（Kmeans中的K），即多少个聚类是最好的。该方法比较直观的理解就是，它可以找到一个K使得这个模型已经很好了，添加更多的聚类对结果影响不大，那么当前这个K就是一个比较合适的值.

首先对比一下两种模型

#设置数据
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
blob_centers = np.array(    
[[ 0.2,  2.3],     
[-1.5 ,  2.3],     
[-2.8,  1.8],     
[-2.8,  2.8],     
[-2.8,  1.3]])
blob_std = np.array([0.4, 0.3, 0.1, 0.1, 0.1])
X, y = make_blobs(n_samples=2000, centers=blob_centers,cluster_std=blob_std, random_state=7)

然后要写一个可以画决策边界的函数，这里还不是elbow method，只是简单对比一下不同K值的两个模型:

def plot_decision_boundary(clf , X):
    mins = X.min(axis=0) - 0.1
    maxs = X.max(axis=0) + 0.1
    xp=np.linspace(mins[0], maxs[0], 500) 
    yp=np.linspace(mins[1], maxs[1], 500) 
    x1, y1=np.meshgrid(xp, yp) 
    xy=np.c_[x1.ravel(), y1.ravel()] 
    
    labels=clf.fit_predict(X)
    
    y_pred = clf.predict(xy).reshape(x1.shape) 
    
    plt.contourf(x1, y1, y_pred, alpha=0.3, cmap=plt.cm.brg)
    #画中心点
    centers=clf.cluster_centers_
    plt.scatter(centers[:,0], centers[:,1], s=200,c='red',alpha=0.5,zorder=2)
    #zorder数值大的会显示在上面
    plt.scatter(X[:,0], X[:,1], c=labels, cmap='viridis',s=20,zorder=1)
    plt.show()

然后对比两个模型

kmeans_k3 = KMeans(n_clusters=3, random_state=42)
kmeans_k8 = KMeans(n_clusters=8, random_state=42)
plot_decision_boundary(kmeans_k3, X) 
plot_decision_boundary(kmeans_k8, X)

结果如下：

我们虽然可以调用模型的inertia参数，但随着K增大，inertia肯定会减少，但由于它是连续递减的，我们需要找到一个递减的”差不多“的位置。

代码实现

kmeans_per_k = [KMeans(n_clusters=k, random_state=42).fit(X)
                for k in range(1, 10)]
inertias = [model.inertia_ for model in kmeans_per_k]
plt.plot(range(1,10), inertias, 'bo-')
plt.xlabel("$k$", fontsize=14)
plt.ylabel("Inertia", fontsize=14)

生成图像，有点类似于梯度下降：

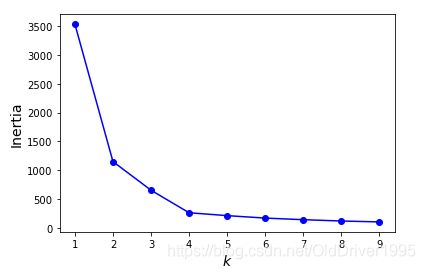
发现k=4的时候就已经下降的很缓慢了。看一下k=4的分类效果：
这里只是比较直观的选择了K，实际上选择的时候需要一定的计算，不过这里省略了这一过程。

silhouette analysis

侧影分析，他的原理是基于相似度计算实现的，计算某一个点和它同一个cluster的其他点的相似度，以及和其他cluster中每个点的相似度，然后会获得一个介于-1到1之间的silhouette score。这个数值越接近1，则说明这个点和同cluster的点越接近，和其他cluster中的点越远（距离上的远近）

然后每个点的score取平均，获得整个模型的score，越接近与1，说明模型越好。

首先plot一下图像：

from sklearn.metrics import silhouette_score
silhouette_scores = [silhouette_score(X, model.labels_)for model in kmeans_per_k[1:]]
plt.plot(range(2, 10), silhouette_scores, "bo-")
plt.xlabel("$k$", fontsize=14)
plt.ylabel("Silhouette score", fontsize=14)

import matplotlib as mpl
from sklearn.metrics import silhouette_samples
from matplotlib.ticker import FixedLocator, FixedFormatter
plt.figure(figsize=(10, 8))

for k in (3, 4, 5, 6):
    plt.subplot(2, 2, k - 2)
    plt.subplots_adjust(hspace=0.5)
    y_pred = kmeans_per_k[k - 1].labels_
    silhouette_coefficients = silhouette_samples(X, y_pred)
    padding = len(X) // 30
    pos = padding
    ticks = []
    
    for i in range(k):
        coeffs = silhouette_coefficients[y_pred == i]
        coeffs.sort()
        color = mpl.cm.Spectral(i / k)
        plt.fill_betweenx(np.arange(pos, pos + len(coeffs)), 0, coeffs, facecolor=color, edgecolor=color, alpha=0.7)
        ticks.append(pos + len(coeffs) // 2)
        pos += len(coeffs) + padding	
        
    plt.gca().yaxis.set_major_locator(FixedLocator(ticks))
    plt.gca().yaxis.set_major_formatter(FixedFormatter(range(k)))
    
    if k in (3, 5):
        plt.ylabel("Cluster")
    if k in (3, 4, 5, 6):
        plt.gca().set_xticks([-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1])
        plt.xlabel("Silhouette Coefficient")
    else:
        plt.tick_params(labelbottom=False)
        
    plt.axvline(x=silhouette_scores[k - 2], color="red", linestyle="--")
    plt.title("$k={}$".format(k), fontsize=16)
    
plt.show()

结果如下：

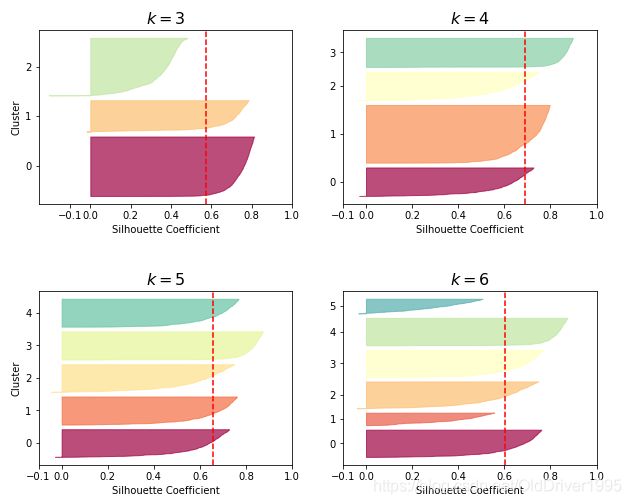
可以看出K=4的时候，silhouette score是最高的，尽管K=5中每个cluster更加均匀。和之前的elbow method的方法所得到的结果相符。