【吴恩达机器学习笔记】八、应用机器学习的建议
✍个人博客:https://blog.csdn.net/Newin2020?spm=1011.2415.3001.5343
专栏定位:为学习吴恩达机器学习视频的同学提供的随堂笔记。
专栏简介:在这个专栏,我将整理吴恩达机器学习视频的所有内容的笔记,方便大家参考学习。
专栏地址:https://blog.csdn.net/Newin2020/article/details/128125806
视频地址:吴恩达机器学习系列课程
❤️如果有收获的话,欢迎点赞收藏,您的支持就是我创作的最大动力
八、应用机器学习的建议
1. 决定下一步要做什么
假如你现在想用一个常规的线性回归算法去预测房屋的价格,但是你发现预测的结果与实际结果偏差很大,那么你可以考虑下面的这几点:
- 尝试获得更多的数据集去训练模型。
- 尝试减少的特征值,有时可能会因为过拟合导致结果不精确。
- 尝试增加的特征值,有时可能项目太大,但是特征值太少。
- 尝试增加多项式特征(x12,x22,x1x2等)。
- 尝试增加λ值。
- 尝试减小λ值。
当然,有时候你可能做完了项目才发现某些算法并不理想,所以后面的内容将介绍该如何排除一些不适合的算法,并且告诉你上面这些方法可以用来解决哪些问题。
2. 评估假设函数
这节课,我们来讲讲该如何去评估你的假设函数,因为有时候误差很小并不是一件好事,可能是过拟合了,当特征量特别多的时候,就很难通过画图去评估假设函数,所以要用到接下来要讲的方法。
首先,对于数据集的处理,我们可以分为两个部分:
一部分为训练集,一部分为测试集,而我们通常将训练集和测试集按照7:3的比例进行划分,这里要注意,所划分的数据集要是随机的。
训练和测试线性回归的步骤:
- 将70%的数据集拿去训练,然后计算出最小的训练误差,得到θ值。
- 计算测试误差。
训练和测试逻辑回归的步骤:
- 将70%的数据集拿去训练,然后计算出最小的训练误差,得到θ值。
- 计算测试误差。
还有一种度量方式是0/1错误分类度量(Misclassification error),可能更好理解一些:
- 当err为1时,说明分类错误即当hθ(x)≥0.5时,将y判断成了0。
- 当err为0时,说明此时分类正确。
3. 模型选择和训练、验证、测试集
这节课我们来看看该如何去选择一个合适的模型,首先先来回顾一下之前的模型选择步骤:
我们之前是用训练集来最小化每一个模型得到θ,然后用同一个训练集来测试哪个误差最小,选出最优的那个模型,而其中出现的d代表的是多项式的阶数。我们假设上面模型中最优的是第五个即d=5,但是这个结果可能过于乐观了,因为它只是针对于训练集训练出的结果,如果放在新样本中可能效果就不会那么好了,所以接下来就要引出验证集了。
为了更好的选择模型,我们现在不再只划分两个数据集,而是三个,分别是训练集、交叉验证集(验证集)和测试集,比例通常在6:2:2,并且选择时也是随机选择的。
接下来就可以分别计算出训练/验证/测试误差,然后进行模型选择。
这里和上面不同,虽然还是先用训练集去最小化代价得到θ,但是用于选择模型的数据集变成了验证集,这样就多了一个测试集出来,用于评估所得模型。
4. 诊断偏差和方差
在训练模型的时候,你可能会遇到两种问题,一种就是高偏差问题,一种就是高方差问题,如何判断是否遇到了这两个问题是我们这节课要学的内容,先来看看训练误差和验证误差与多项次数d的关系。
由图中可以看到,当d很小的时候,会处于欠拟合状态,所以训练和验证误差会非常的大,当d很大的时候,训练误差会非常的小因为处于过拟合状态,所以这时候验证误差会变得很大。而在中间能够找到一个合适的d,使验证误差达到最小,所以我们就可以进行总结了。
当训练误差和验证误差都很大的时候,处于欠拟合状态,那就是出现了高偏差问题。
当训练误差很小并且远小于验证误差时,处于过拟合状态,那就是出现了高方差问题。
5. 正则化和偏差、方差
这节课我们来更深入的理解一下正则化和偏差、方差的关系,我们先来看看加了正则化的模型该如何去选择。
这里选择模型需要我们尝试各个λ的值,然后通过验证集去拟合参数计算验证误差得到最优解,假设我们得到的是θ(5),那么我们就可以像上面讲的一样,用测试集来评估这个选出来的模型如何。
接下来我们来看看λ对于J(θ)的曲线的影响如何。
- Jtrain(θ)的值会随着λ的增大而增大,因为λ太小时,就几乎没有正则化,所以会导致过拟合;λ太大时,会对θ的惩罚过大,导致欠拟合。
- Jcv(θ)的值会随着λ的增大先减小后增大,同样当λ太小时,几乎没有正则化,这里就被称为高方差问题,而太大时就被称为高偏差问题,在中间就可以找到一个合适的λ值去拟合数据。
6. 学习曲线
假设我们用一个二次函数来拟合我们的数据,并且人为的控制数据量来观察h(θ)的拟合情况。
从上图右边的图像可以看出,在m很小的时候即数量集只有几个的时候,二次函数可以很好的拟合数据,但是随着m增大,拟合效果会变差。
再来看看Jtrain(θ)随m增大变化如何,从曲线看发现随着m增大Jtrain(θ)也会增大,而Jcv(θ)反而会减小。
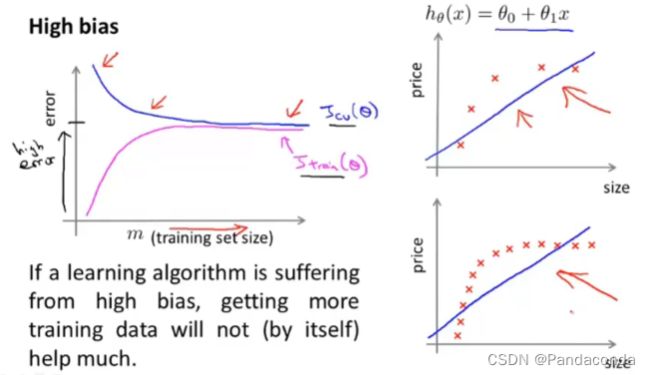
接下来再来看看分别在高偏差和高方差下,曲线的情况,先来看高偏差(High bias)。
你会发现,当m增大到一定程度时,验证误差和训练误差几乎保持不变,所以在高偏差的情况下,一般增大数据集的数量并不能减少误差值。
接下来,再来看看高方差(High variance)。
可以看到当训练集数量增大到一定程度时,训练误差和验证误差也会逐渐相近,并且会接近于比较低的一个点,所以增大训练集的数量对高方差问题是有一定改善的。
7. 决定接下来要做什么
现在,我们就可以总结一下第一节所提到的那些方法可以分别用于什么问题了:
- 尝试获得更多的数据集去训练模型:解决高方差问题。
- 尝试减少的特征值,有时可能会因为过拟合导致结果不精确:解决高方差问题
- 尝试增加的特征值,有时可能项目太大,但是特征值太少:解决高偏差问题。
- 尝试增加多项式特征(x12,x22,x1x2等):解决高偏差问题。
- 尝试增加λ值:解决高方差问题。
- 尝试减小λ值:解决高偏差问题。
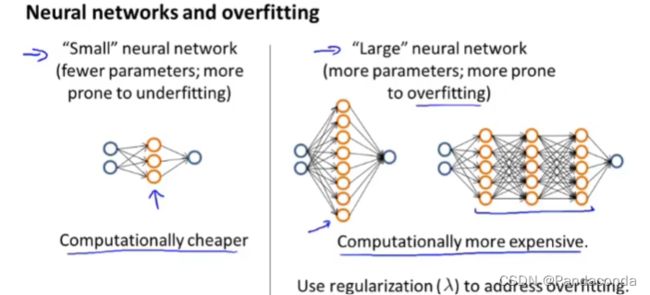
然后我们再来看看神经网络:
如果你选择一个较小的神经网络,你的计算量就会非常的小,参数也会很少,而且会更容易欠拟合。
如果你选择一个较大的神经网络,你的计算量就会非常的大,参数也会很多,而且会更容易过拟合,但是我们一般宁愿选择一个较大的神经网络而不是较小的神经网路是因为,过拟合时你可以用正则化来改善过拟合的问题。