IJCAI 2018: Globally Optimized Mutual Influence Aware Ranking in E-Commerce Search (面向搜索的互影响感知排序)

0. 摘要

在网页搜索中，从搜索结果多样化的角度研究了文档之间的相互影响。但是网页搜索中的方法因其不同而不能直接应用于电子商务搜索。而对电子商务搜索中item间的相互影响的研究很少。我们提出了一个在电子商务搜索中互影响感知排序的全局优化框架。我们的框架直接优化总商品量(GMV)进行排名，并将排名分解为两个任务。第一个任务是互影响感知购买概率估计。我们提出了一种全局特征扩展方法，将互影响融入到item的特征中。我们还使用递归神经网络(RNN)来捕捉与采购概率估计中的订单排序相关的影响。第二个任务是根据购买概率估计找到最佳排名顺序。我们将第二个任务视为序列生成问题，并使用beam search算法来解决它。我们在一个大型电商搜索引擎上进行了在线A/B测试。结果表明，我们的方法为搜索引擎带来了5%的增长，超过了强基线。

1. 动机

1. 在网络搜索中，文档之间相互影响的重要性早就被认识到了，并且已经从搜索结果多样化的角度进行了研究，因为相关性和多样性是网络搜索的主要关注点。然而电子商务搜索中相关研究却很少。
2. 电子商务搜索中项目之间的相互影响与网页搜索是非常不同的，搜索结果的多样性并不是电子商务搜索的主要关注点。
3. 互影响在电子搜索中是很重要的 。当客户在大型电子商务平台上发布查询时，通常会返回数千个高度相关的项目。客户的比较通常不是基于相关性，因为所有项目都是高度相关的，而是基于一个项目的几个细节方面，例如价格、品牌、质量等。如果一件商品被其他质量相似但价格高得多的商品包围，那么它被购买的可能性就会很高。相反，如果同一件物品周围都是价格低得多的物品，那么它被购买的可能性就会更低。

2. 贡献

1. 我们首次提出了一个电子商务搜索中互影响感知排序的框架。我们将排名表述为一个全局优化问题，目标是最大化GMV的数学期望。在我们的框架中，在购买概率估计模型中考虑了项目之间的互影响，该模型预测项目是否会被购买。我们首先提出一种全局特征扩展方法，将互影响融入到项目的特征中。我们使用DNN来估计基于扩展特征的购买概率。利用我们的DNN模型，通过简单的排序就可以找到最优的排名。此外，我们使用RNN来考虑与排名顺序相关的相互影响。
2. 我们设计了一种新的注意力机制来适应项目之间的长距离影响。通过我们的RNN模型，我们的全局优化框架变成了序列生成问题。我们使用beam search算法来生成一个好的排名。我们在全球最大的电商搜索引擎之一淘宝搜索上进行了在线A/B测试。我们将我们方法的GMV和计算成本与一个强基线进行了比较。结果表明，在可接受的计算成本下，我们的方法使GMV比基线增加了5%，这被认为是一个非常大的改进。

3. 模型

3.1 问题定式

项目集合：$S=(1,2,3,...,N)$
项目中的一种排列：$o=(o_1,o_2,...,o_N)\in O$
对于项目$i$的购买率，受到来自其他项目的影响，称为排名上下文：$c(o，i)=(o1，...O_{d_i-1}，o_{d_i+1}，...，o_N)$。
对于排列$o$的商品$i$的购买率为：$p(i|c(o,i))$
商品$i$的销售价值为：$v(i)$
那么排列$o$的预期GMV：

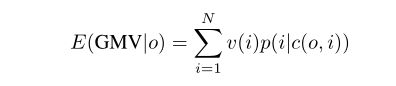
排名的目标是找到一个排列，最大化预期的GMV:

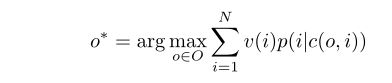
整个工作可以分为两个问题：
问题1：如何准确估计购买率$p(i|c(o，i))$。
问题2：如何高效地找到排列$o^{\ast }$。

作者给出两种解决方案。

3.2 全局特征扩展

我们只考虑排序上下文中的项目集，即$c(o，i)=S$。排序顺序在$c(o，I)$中被忽略。在排序中，项I由一个特征向量$f_l(i)$表示，我们称之为的局部特征。通常$f_l(i)$的每个维数都是一个实值数。在这种简化中，其他项对I的影响由全局特征向量$f_g(i)$表示。我们将局部和全局特征连接成$f(i)=(f_l(i)，f_g(i))$。并用$f(i)$预测$p(i|c(o，i))$。我们称$f(i)$为$i$项的全局特征扩展。

项目的全局特征生成如下。让我们以价格特征为例。我们可以将项目$i$的价格与其他人的价格进行比较，看看$i$在$S$中是否昂贵。这样将得到$i$在$S$中的相对“昂贵性”。同样，我们以这种方式将$i$的每个局部特征与其他特征进行比较，并获得全局特征向量$f_g(i)$:

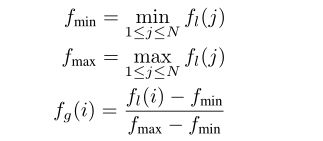
3.3 DNN

全局特征扩展$f(i)$将来自其他项目的影响合并到$i$中。因此，我们将$f(i)$馈送到DNN，以利用互影响感知对$p(i|c(o，i))$进行估计。
我们的DNN有3个隐藏的ReLU层和一个sigmoid输出层，并使用交叉熵损失进行训练。在全局特征扩展过程之后，$p(i|c(o，i))$可以为每个$i$独立计算。然而，在这个模型中没有考虑排名位置。所以位置偏差会是个问题。我们通过将位置偏差乘以我们的模型来纠正这一点，位置偏差是相对于排名位置的递减函数。所以我们不需要知道位置偏差的确切值，因为问题2可以通过用$v(i)p(i|c(o，i))$给每个项目打分，然后按降序排序来解决。
因此，我们得到了一个非常有效的排名方法。总体而言，需要$O(Nd)$时间来进行全局特征扩展，并且需要$O(N)$使得DNN向前运行来找到最优排序。

3.4 RNN

在第二种简化中，当估计$p(i|c(o，i))$时，我们不仅考虑项目集，还考虑项目I之前的排序，即$c(o，i)=(o_1，o_2，...，o_{d_i-1}，S)$。类似于第一种简化，我们使用全局特征扩展。那么我们可以写$p(i|c(o，i))=p(i|o_1，o_2，...o_{d_i-1})$，因为$S$已经被全局特性扩展考虑到了。基于订单排序在I之前估计符合客户的浏览习惯，因为客户通常以自上而下的方式进行浏览。我之后的排名顺序没有被考虑，主要是因为这将打破顺序选择过程，这支持有效的增量计算。

现在问题1变成了顺序概率估计问题。用RNN模型估计。如下计算估计概率:

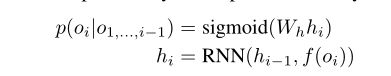
问题2现在变成了序列生成问题，类似于机器翻译中的解码过。不同的是，我们需要最大化预期的GMV，$S$中的每个项目必须在序列中恰好出现一次。尽管存在差异，有效的beam search算法仍然可以适用于解决问题2。beam search是贪婪搜索算法的推广。beam search在选择的每一步都保留前$k$个序列，并在最后一步返回最佳序列。用于排序的beam search算法在算法1中给出：

算法1的时间复杂度是$O(k{N}^2)$，虽然二次时间复杂度通常对排名来说太昂贵，但我们可以在只有前$N$个项目被重新排名的重新排名过程中使用它。详情将在第4.3节中解释。为了清楚起见，我们beam search仅用于在线排名。RNN模型的训练不需要使用波束搜索。

但在实践中，我们发现LSTM无法学习长期依赖。我们用RNN计算了很多序列中第20位的购买概率，例如排名前4位的物品对第20位物品的购买概率影响不大。这是不合理的，因为顾客通常对排名靠前的商品有强烈的印象。来自最重要项目的影响不容忽视。为了克服这个问题，我们设计了一个RNN模型的注意机制，灵感来自于神经机器翻译的工作。网络结构如图1所示。在我们的注意机制中，$p(o_i|o_{1，...i-1})$不仅取决于当前隐藏向量$h_i$，还取决于所有先前隐藏向量的加权和。

公式如下：

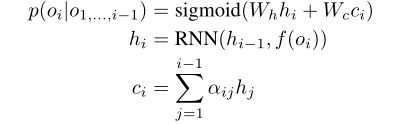
利用RNN注意模型，我们仍然使用beam search来找到一个好的排序序列。。但是注意机制需要更多的计算。算法1的时间复杂度变为$O(k{N}^3)$。

4. 实验

实验是在淘宝搜索平台上进行的，这是世界上最大的电子商务搜索服务之一，日志中的每条记录对应于一个查询，并包含呈现给客户的项目。购买的物品是阳性样品，其他是阴性样品。阳性样本比阴性样本少得多。为了平衡阳性和阴性样本的数量，我们会丢弃所有不包含购买的记录。所以在我们的培训数据中，每条记录至少包含一次购买。这样做，我们不仅减少了负样本的数量，还排除了那些用户没有购买意向，只是为了好玩而浏览的记录。在在线测试中，我们每天更新我们的模型，并使用最后一天的日志数据进行培训。

项目的本地特征包括价格、与查询的相关性、点击率(CTR)、点击购买转化率(CVR)和各种用户偏好分数，例如品牌或商店偏好等。除了价格特征之外，每个局部特征都是由较低级别的模型产生的。大多数低级模型使用大量低级特征，例如相关性模型使用查询词和项目标题作为特征。我们的排名模型建立在这些局部特征的基础上，因此不需要使用大量的低级特征。事实上，我们在购买概率模型中只使用了23个局部特征。

4.1 购买概率估计的评估

我们使用ROC曲线下面积(AUC)和相对信息增益(RIG)指标进行评估。测试数据的结果如表1所示。

注意力可视化如下图所示：排名靠前的项目也有更大的关注度。这意味着我们注意力集中的RNN学会了考虑排名靠前的项目的影响，即使是在估计一个排名远低于它的项目的概率时。因此，注意力机制确实缓解了我们提到的远距离依赖问题。

4.2 在线A/B测试

根据统计所示，用户平均浏览项目数为52。这意味着只有排名靠前的项目才是真正重要的。正如我们在第3节中所述，miRNN和MiRNN+Attention的时间复杂度是太高。出于对计算效率的实际考虑，RNN模型不应排列太多项目。因此，我们在在线测试的重新排序过程中使用我们的模型。具体来说，我们使用我们的模型对基线排名的前N项进行重新排序。并将我们的模型的gmv与基线进行了比较。

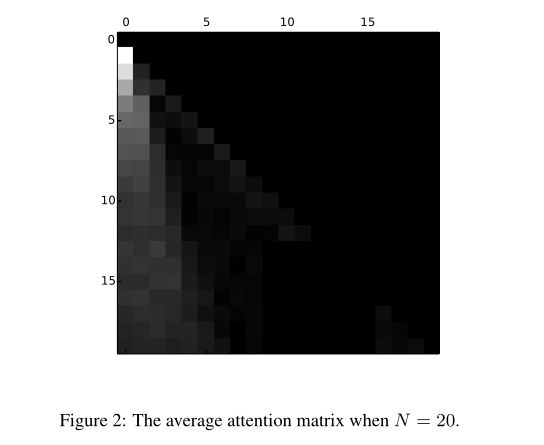
下图显示我们的模型在基线上显著增加了GMV。我们模型的GMV随着重新排序大小的增加而增加，但是随着重新排序大小变得大于50而逐渐稳定。

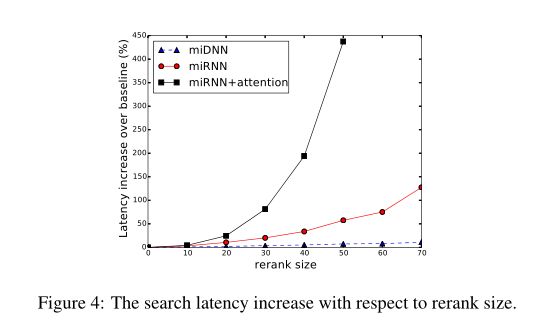
在下图中，miDNN的延迟很小，并且相对于重新排序的大小呈线性增长。但是miRNN和miRNN+Attention的延迟是多项式增长的。当重新排序大小为50时，MiRNn+注意力的延迟比基线增加了400%，从21毫秒增加到105毫秒。虽然RNN模型实现了更大的GMV，但是当重新排序大小变大时，RNN模型的计算成本是巨大的。庞大的计算成本是我们的RNN模型的主要缺点。

5. 思考

其实模型无论DNN还是RNN都是训练的一个预测购买率的情况。

DNN训练和预测购买概率都很好理解，最终预测输入是一个item随机序列，那么DNN输出每个Item的购买概率之后还要乘以位置偏重为最后的购买概率估计。
RNN的话按我理解应该在训练时，输入是一个item序列，label是对应的购买概率序列。不用beam search；在预测购买概率的时候，RNN也是输入一个item的随机拜访序列，然后来预测这个序列所对应的购买概率序列，可能也用不到beam search（我理解DNN和RNN在预测购买概率时都没有进行重排）；当然也可以理解为预测时，DNN和RNN也可以利用各自的重排方案重排以后得到最优的item序列，再得到购买概率预测。

DNN和RNN模型如果能很好的掌握购买概率估计，就能很好的进行重排来提高GMV了。DNN其实预测得到概率以后然后进行重排的，概率*单价高的在前面。RNN就是通过beam search，保存当前生成的GMV最高的那K个摆放item序列。

这篇文章中一个是互影响的加入，这里有些可以深究的点。他这个互影响并没有考虑相对位置的关系，该论文中将所有的item都当作一个set计算互影响，按理说离该item距离近的那些商品影响更大一点，或者说比较靠前的item影响比较大，所以当作set计算互影响可能不太合理，应该更好的利用相对位置关系。
当然论文中RNN+attention在评估当前物体的购买概率时，一定程度上利用到了排在前面物体的特征，并自适应的寻找对比依赖权重，弥补了互影响特征建模的不足，可能这也是为什么RNN比DNN效果优越的原因。

或许在DNN中互影响的建模更精细一点（考虑到人们购买时的上下文商品对比以及排名靠前的博人眼球），可能效果会更好，并且延时远远低于RNN。