基于粒子群优化算法的p-Hub选址优化（Matlab代码实现）

目录

1 概述

2 运行结果

2.1 算例1

2.2 算例2 

2.3 算例3

3 参考文献

4 Matlab代码及详细文章

---

1 概述

位置一分配问题起源于美国民用航空局(CAB),其航空公司航线的结构为轴辐系统(Hub-and-Spoke),以某一个主要的机场为轴(Hub),众多由此辐射而出的航线为辐(Spoke),在中枢的主要机场看成一个转运点,从而提供旅客和货物的转运.其中 P-Hub中心问题即是轴辐系统的一种,该问题已广泛应用在现实生活中,如航线问题、邮件传送问题、货物运送问题、通讯问题等.

部分代码：

function sol=ParseSolution(xhat,model)

    N=model.N;
    P=model.P;
    c=model.c;
    alpha=model.alpha;
    f=model.f;
    r=model.r;

    xii=diag(xhat)';
    
    if any(xii>=0.5)
        
        [~, so]=sort(xii,'descend');
        
        nHub=0;
        for i=so
            if xii(i)<0.5 || nHub>=P
                break;
            end
            
            xii(i)=1;
            
            nHub=nHub+1;
        end
        
        xii(xii<1)=0;
        
    else
        
        [~, imax]=max(xii);
        
        xii(:)=0;
        xii(imax)=1;
        
    end
    
    Hubs=find(xii==1);
    
    x=xhat;
    for i=1:N
        if xii(i)==0
            x(i,:)=0;
        else
            x(:,i)=0;
            x(i,i)=1;
        end
    end
    
    h=zeros(1,N);
    for i=1:N
        
        XI=x(:,i);
        XI(xii==0)=-inf;
        
        [~, h(i)]=max(XI);
        
        x(:,i)=0;
        x(h(i),i)=1;
        
    end
    
    oc=zeros(N,N);
    for i=1:N
        for j=1:N
            if i==j
                oc(i,j)=0;
            else
                k=h(i);
                l=h(j);
                oc(i,j)=c(i,k)+alpha*c(k,l)+c(l,j);
            end
        end
    end
    
    ocr=oc.*r;
    SumOCR=sum(ocr(:));
    
    xiif=xii.*f;
    SumXF=sum(xiif);
    
    TotalCost=SumOCR+SumXF;
    
    sol.x=x;
    sol.h=h;
    sol.Hubs=Hubs;
    sol.SumOCR=SumOCR;
    sol.SumXF=SumXF;
    sol.TotalCost=TotalCost;

end

function sol=ParseSolution(xhat,model)

    N=model.N;
    P=model.P;
    c=model.c;
    alpha=model.alpha;
    f=model.f;
    r=model.r;

    xii=diag(xhat)';
    
    if any(xii>=0.5)
        
        [~, so]=sort(xii,'descend');
        
        nHub=0;
        for i=so
            if xii(i)<0.5 || nHub>=P
                break;
            end
            
            xii(i)=1;
            
            nHub=nHub+1;
        end
        
        xii(xii<1)=0;
        
    else
        
        [~, imax]=max(xii);
        
        xii(:)=0;
        xii(imax)=1;
        
    end
    
    Hubs=find(xii==1);
    
    x=xhat;
    for i=1:N
        if xii(i)==0
            x(i,:)=0;
        else
            x(:,i)=0;
            x(i,i)=1;
        end
    end
    
    h=zeros(1,N);
    for i=1:N
        
        XI=x(:,i);
        XI(xii==0)=-inf;
        
        [~, h(i)]=max(XI);
        
        x(:,i)=0;
        x(h(i),i)=1;
        
    end
    
    oc=zeros(N,N);
    for i=1:N
        for j=1:N
            if i==j
                oc(i,j)=0;
            else
                k=h(i);
                l=h(j);
                oc(i,j)=c(i,k)+alpha*c(k,l)+c(l,j);
            end
        end
    end
    
    ocr=oc.*r;
    SumOCR=sum(ocr(:));
    
    xiif=xii.*f;
    SumXF=sum(xiif);
    
    TotalCost=SumOCR+SumXF;
    
    sol.x=x;
    sol.h=h;
    sol.Hubs=Hubs;
    sol.SumOCR=SumOCR;
    sol.SumXF=SumXF;
    sol.TotalCost=TotalCost;

end

function sol=ParseSolution(xhat,model)

    N=model.N;
    P=model.P;
    c=model.c;
    alpha=model.alpha;
    f=model.f;
    r=model.r;

    xii=diag(xhat)';
    
    if any(xii>=0.5)
        
        [~, so]=sort(xii,'descend');
        
        nHub=0;
        for i=so
            if xii(i)<0.5 || nHub>=P
                break;
            end
            
            xii(i)=1;
            
            nHub=nHub+1;
        end
        
        xii(xii<1)=0;
        
    else
        
        [~, imax]=max(xii);
        
        xii(:)=0;
        xii(imax)=1;
        
    end
    
    Hubs=find(xii==1);
    
    x=xhat;
    for i=1:N
        if xii(i)==0
            x(i,:)=0;
        else
            x(:,i)=0;
            x(i,i)=1;
        end
    end
    
    h=zeros(1,N);
    for i=1:N
        
        XI=x(:,i);
        XI(xii==0)=-inf;
        
        [~, h(i)]=max(XI);
        
        x(:,i)=0;
        x(h(i),i)=1;
        
    end
    
    oc=zeros(N,N);
    for i=1:N
        for j=1:N
            if i==j
                oc(i,j)=0;
            else
                k=h(i);
                l=h(j);
                oc(i,j)=c(i,k)+alpha*c(k,l)+c(l,j);
            end
        end
    end
    
    ocr=oc.*r;
    SumOCR=sum(ocr(:));
    
    xiif=xii.*f;
    SumXF=sum(xiif);
    
    TotalCost=SumOCR+SumXF;
    
    sol.x=x;
    sol.h=h;
    sol.Hubs=Hubs;
    sol.SumOCR=SumOCR;
    sol.SumXF=SumXF;
    sol.TotalCost=TotalCost;

end

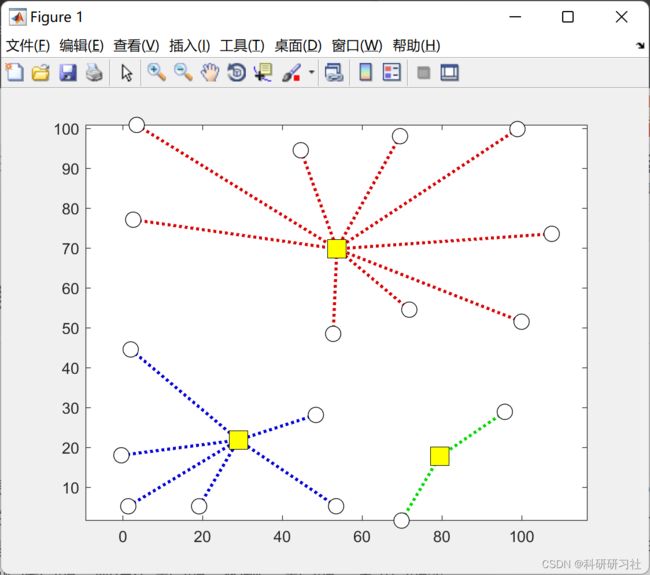
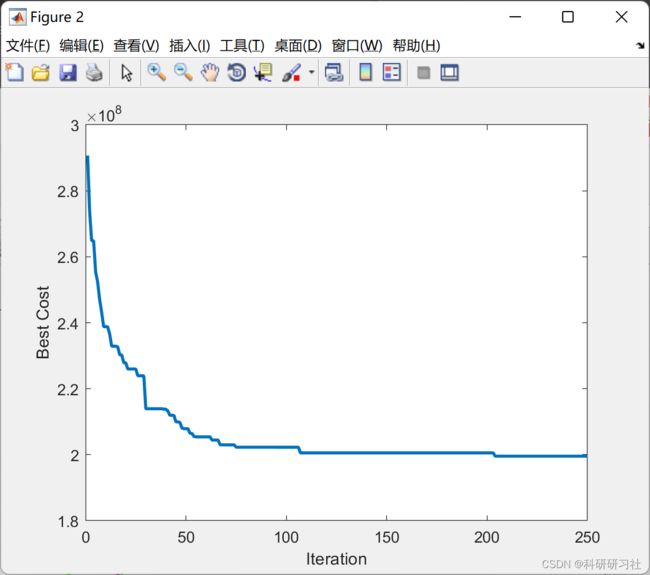
2 运行结果

2.1 算例1

2.2 算例2 

 

2.3 算例3

 

3 参考文献

部分理论引用网络文献，如有侵权请联系删除。

[1]卓月明,樊晓兵.基于SOFM的P-Hub中心问题的最优求解.吉首大学学报：自然科学版,2009(5):60-63
机构:吉首大学物理科学与信息工程学院
摘要:"位置-分配问题"是运输问题中一个重要的研究问题,其中P-Hub中心问题被广泛的应用在航空、通讯、邮件送发问题上.目前已有许多启发式的方法被广泛应用求最优解,如基因算法、模拟退火法、Hopfield network等;本研究针对顾客及服务中心数目已知的条件下,提出了基于人工神经网络的自组织特征映射网络求解方法,运用神经元的自我学习功能来找出最佳的服务中心位置.

4 Matlab代码及详细文章

博客主页：@橘柑橙柠桔柚