scipy.optimize.curve_fit-曲线拟合

Scipy是一个用于数学、科学、工程领域的常用软件包，可以处理插值、积分、优化、图像处理、常微分方程数值解的求解、信号处理等问题。它用于有效计算Numpy矩阵，使Numpy和Scipy协同工作，高效解决问题。

scipy.optimize中有curve_fit方法可以拟合自定义的曲线，如指数函数拟合，幂指函数拟合和多项式拟合，下面导入相应的包进行拟合的一个例子：

导入需要的包

from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['SimHei']
%matplotlib inline # jupyter notebook图像显示设置
%config InlineBackend.figure_format = 'svg' # jupyter notebook图像矢量图设置

自定义函数拟合

# 自定义函数，curve_fit支持自定义函数的形式进行拟合，这里定义的是指数函数的形式
# 包括自变量x和a，b，c三个参数
def func(x, a, b, c):
    return a * np.exp(-b * x) + c

# 产生数据
xdata = np.linspace(0, 4, 50) # x从0到4取50个点
y = func(xdata, 2.5, 1.3, 0.5) # 在x取xdata，a，b，c分别取2.5, 1.3, 0.5条件下，运用自定义函数计算y的值

# 在y上产生一些扰动模拟真实数据
np.random.seed(1729)
# 产生均值为0，标准差为1，维度为xdata大小的正态分布随机抽样0.2倍的扰动
y_noise = 0.2 * np.random.normal(size=xdata.size) 
ydata = y + y_noise
plt.plot(xdata, ydata, 'b-', label='data')

# 利用“真实”数据进行曲线拟合
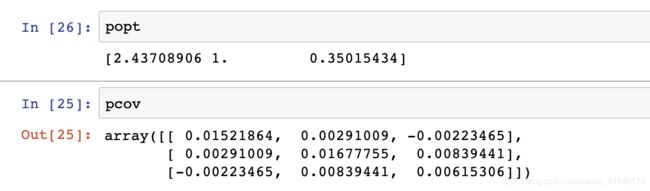
popt, pcov = curve_fit(func, xdata, ydata) # 拟合方程，参数包括func，xdata，ydata，
# 有popt和pcov两个个参数，其中popt参数为a，b，c，pcov为拟合参数的协方差

# plot出拟合曲线，其中的y使用拟合方程和xdata求出
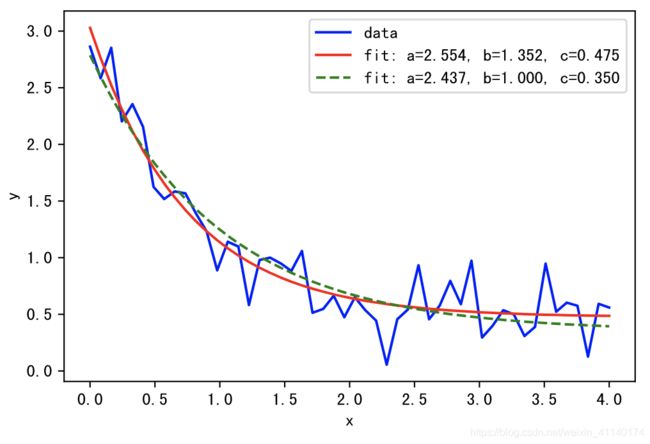
plt.plot(xdata, func(xdata, *popt), 'r-',
         label='fit: a=%5.3f, b=%5.3f, c=%5.3f' % tuple(popt))
    

#     如果参数本身有范围，则可以设置参数的范围，如 0 <= a <= 3,
#     0 <= b <= 1 and 0 <= c <= 0.5:
popt, pcov = curve_fit(func, xdata, ydata, bounds=(0, [3., 1., 0.5])) # bounds为限定a，b，c参数的范围

plt.plot(xdata, func(xdata, *popt), 'g--',
              label='fit: a=%5.3f, b=%5.3f, c=%5.3f' % tuple(popt))
    
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()

结果展示

popt为限定参数a，b，c的参数拟合值

函数参数设置

scipy.optimize.curve_fit(f, xdata, ydata, p0=None, sigma=None, absolute_sigma=False, check_finite=True, bounds=- inf, inf, method=None, jac=None, **kwargs)[source]

f: 函数形式

xdata：自变量x，一般为数组或者向量

ydata：应变量y，一般为一维数组

bounds：参数的范围设置

具体参数设置见：

https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.curve_fit.html

散点图显示拟合方程及R2

# 画散点图并标记拟合方程以及R2
from scipy.optimize import curve_fit
def curve_fitting(data, x_col,y_col):
    # 自定义函数，curve_fit支持自定义函数的形式进行拟合，这里定义的是指数函数的形式
    def func(x, a, b):
        return a * x + b
    xdata = data[x_col]
    ydata = data[y_col]

    # 利用“真实”数据进行曲线拟合
    popt, pcov = curve_fit(func, xdata, ydata) # 拟合方程，参数包括func，xdata，ydata
    # 有popt和pcov两个个参数，其中popt参数为a，b，c，pcov为拟合参数的协方差

    plt.scatter(xdata,ydata)
    plt.plot(xdata, func(xdata, *popt), 'b-',
             label='y = %5.2f * x + %5.2f' % (tuple(popt)))
    plt.plot(xdata, func(xdata, *popt), 'b-',
             label='R2:%5.2f' % (np.corrcoef(ydata,func(xdata,*popt))[0,1]**2))
    
    plt.xlabel(x_col)
    plt.ylabel(y_col)
    plt.legend()


# 调用函数
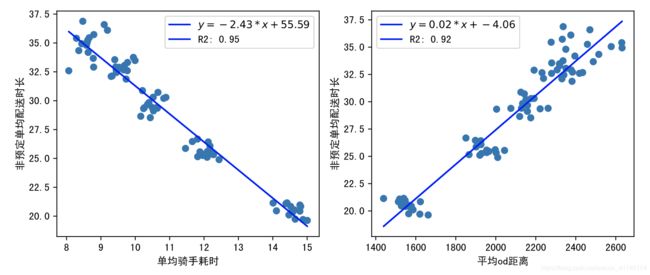
# data为画图数据的dataframe，x_col='单均骑手耗时',y_col = '非预定单均配送时长'
fig,ax = plt.subplots(1,2,figsize=(10,4))
plt.subplot(121)
curve_fitting(data,'单均骑手耗时','非预定单均配送时长')

plt.subplot(122)
curve_fitting(data,'平均od距离','非预定单均配送时长')