(NLP) Predicting trigonometric functions with RNNs

Today I want to organize what I have learned about RNNs in the form of my blog.

1. Key point

RNNs are neural networks being affected by h(t-1) and x(t).

What is h(t-1) and x(t)?

This is my vivid answer. When we were in childhood, our parents used to request us to recite the textbooks. There is a sentence below.

“Let perseverance be your engine and hope your fuel!”
“의지력이 당신의 동력이여 희망은 연료로 되어라!”
“让毅力成为你的引擎，让希望成为你的燃料！”
Let’s start! how can you recite this sentence?

1. You will only recite one word at a time, with only one individual word in your head. When your parents test you you can only memorize individual words that are divided from each other.
   Let… ??? be ??? your ??? ??? fuel. (PS: This is a purely linear layer if we think in terms of neural networks.Using linear layers for long sequences has the following drawbacks. The first is that there are too many parameters[w, b]. The second point is that contextual information cannot be preserved.)
2. You can recall a word you have memorized before you start to recite the word of the moment, and continue in this way. When you recite the word “perseverance” you need to recall the word “let” first. In other words, you need to remember what happened a moment before the current time.

To sum up, " perseverance " means x(t). When the moment t is the word “perseverance” you want to recite, the “Let” in your mind the moment before is h(t-1). The point is that the word must be in your mind and be absorbed into your cells, if not, it is simply x(t-1).

From here

2. Using RNNs to predict the sin function.

import numpy as np
import torch
from torch import nn
import torch.optim as optim
from matplotlib import pyplot as plt

import os
os.environ["KMP_DUPLICATE_LIB_OK"]="TRUE"

num_time_steps = 50
input_size = 1
hidden_size = 16
output_size = 1
lr = 0.01

class Net(nn.Module):
    def __init__(self):
        super().__init__()
        self.rnn = nn.RNN(
            input_size=input_size,
            hidden_size=hidden_size,
            num_layers=1,
            batch_first=True,
        )

        for p in self.rnn.parameters():
            nn.init.normal_(p, mean=0.0, std=0.001)

        self.linear = nn.Linear(hidden_size, output_size)

    def forward(self, x, hidden_prev):
        out, hidden_prev = self.rnn(x, hidden_prev)
        # [1, seq, h] => [seq, h]
        out = out.view(-1, hidden_size)
        out = self.linear(out) # [seq, h] => [seq, 1]
        out = out.unsqueeze(dim=0) # => [1, seq, 1]
        return out, hidden_prev


model = Net()
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr)

hidden_prev = torch.zeros(1, 1, hidden_size)

for iter in range(6000):
    start = np.random.randint(3, size=1)[0]
    time_steps = np.linspace(start, start+10, num_time_steps)
    data = np.sin(time_steps)
    data = data.reshape(num_time_steps, 1)
    x = torch.tensor(data[:-1]).float().view(1, num_time_steps -1, 1)
    y = torch.tensor(data[1:]).float().view(1, num_time_steps -1, 1)

    output, hidden_prev = model(x, hidden_prev)
    hidden_prev = hidden_prev.detach()

    loss = criterion(output, y)
    model.zero_grad()
    loss.backward()
    optimizer.step()

    if iter % 100 ==0:
        print(f"Iteration:{iter}  loss{loss.item()}")

start = np.random.randint(3, size=1)[0]
time_steps = np.linspace(start, start + 10, num_time_steps)
data = np.sin(time_steps)
data = data.reshape(num_time_steps, 1)
x = torch.tensor(data[:-1]).float().view(1, num_time_steps - 1, 1)
y = torch.tensor(data[1:]).float().view(1, num_time_steps - 1, 1)

predictions = []
input = x[:, 0, :]
for _ in range(x.shape[1]):
    input = input.view(1, 1, 1)
    (pred, hidden_prev) = model(input, hidden_prev)
    input = pred
    predictions.append(pred.detach().numpy().ravel()[0])

x = x.data.numpy().ravel()
y = y.data.numpy()
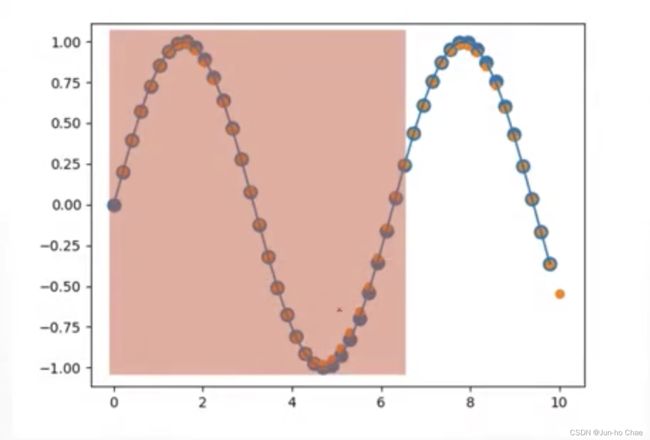
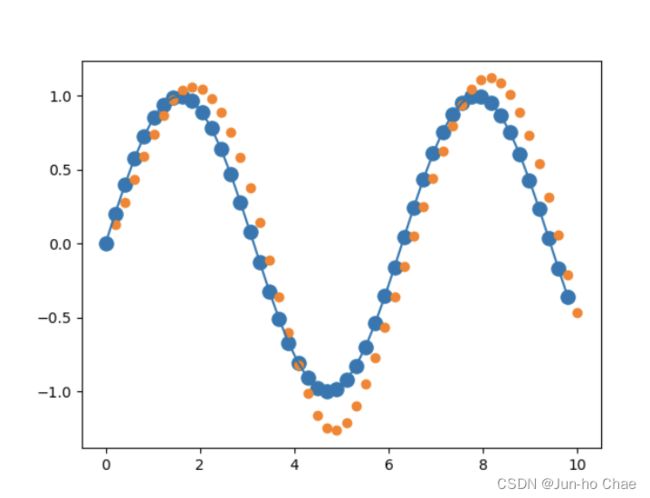
plt.scatter(time_steps[:-1], x.ravel(), s=90)
plt.plot(time_steps[:-1], x.ravel())

plt.scatter(time_steps[1:], predictions)
plt.show()

If you get this ERROR below.

You should be using the following method.

import os
os.environ['KMP_DUPLICATE_LIB_OK']='True'

Finally

Thank you for the current age of knowledge sharing and the people willing to share it, thank you! The knowledge on this blog is what I’ve learned on this site, thanks for the support!