SuperPoint Self-supervised Interest Point Detection and Description
论文地址:https://arxiv.org/abs/1712.07629
代码地址:https://github.com/magicleap/SuperPointPretrainedNetwork
Abstract
本文提出了一个自监督框架,用于训练兴趣点检测器与描述器,适用于多视几何问题。与基于图像块的神经网络不同,本文的全卷积模型使用全尺寸的图像,单次前向计算就可得到像素级的兴趣点位置和相关的描述符。作者引入了单应自适应方法,它一个多尺度、多单应的方法来提升兴趣点检测的再现性,并进行跨域自适应(合成-真实图像)。本文模型通过单应自适应方法,在 MS-COCO 数据集上进行了训练,相较于其它传统模型,可重复检测出更加丰富的兴趣点集合。和 LIFT、SIFT 和 ORB 方法相比,该系统在 HPatches 上能实现 SOTA 的单应预测结果。
1. Introduction
几何计算机视觉任务如 SLAM、SfM、摄像头校准和图像匹配都要先从图像中提取兴趣点。兴趣点就是图像中的点,你从不同的光照条件和视角看过去都稳定而重复出现的点。数学和计算机视觉中有个领域叫多视几何,它的定理和算法都基于一个假设,就是我们可以从多个图片中可靠地提取出兴趣点并匹配起来。但是在现实世界中,计算机视觉系统的输入是原始图像,而不是点的位置。
在几乎所有的图像任务上,CNN 相较于人工特征都具有一定的优越性。在各种任务上(如人体姿态估计、目标检测和空间布局预测),全卷积网络可以预测出 2D 的关键点或 landmarks,得到了广泛的研究。这些技术的核心就是人工标注的数据集,由 2D ground-truth 坐标点组成。
似乎我们也可以将兴趣点检测看作为一个监督机器学习的问题,然后训练一个最新的 CNN 来检测。语义任务如人体关键点预测,会检测出人体的一部分,如嘴角或左脚踝,但兴趣点的语义定义并不清晰。因此通过强监督的方式训练 CNN 进行兴趣点检测就没那么简单了。
作者没有使用人工标注的方式来定义图像中的兴趣点,而是通过自训练提出了一个自监督方案。作者构建了一个由图像中伪 ground-truth 兴趣点构成的大规模数据集,监督来自于兴趣点检测器自身,而非大量的人工标注。
为了生成这些伪 ground-truth 兴趣点,作者首先构建了一个合成数据集(叫做 Synthetic Shapes,如图2a所示),包含数百万个样本,然后训练出一个全卷积网络。该数据集由简单的几何形状构成,兴趣点的位置清楚。作者将这个检测器叫做 MagicPoint。在Synthetic Shapes上,MagicPoint 明显优于传统的兴趣点检测器。它在真实图像上的效果也不错,尽管有域自适应的问题。但是在纹理和花纹复杂的图像集合上,与传统的兴趣点检测器相比,MagicPoint 则会漏掉不少潜在的兴趣点。为了解决这个问题,作者设计了一个多尺度、多重变换的方法 — 单应自适应。
单应自适应会用于兴趣点检测器的自监督训练。它将图像变形多次,帮助兴趣点检测器从不同的角度、尺度来看待场景。作者使用单应自适应和 MagicPoint 检测器来提升表现,生成伪 ground-truth 兴趣点(图2b)。检测结果的再现性就更强,产生更多有用的兴趣点;因此将该检测器叫做SuperPoint。
检测出鲁棒、可再现的兴趣点后,最常见的步骤就是给每个点附上一个固定维度的描述向量,然后进行更高级的语义任务,如图像匹配。因此,作者将 SuperPoint 和一个描述器网络结合(图2c)。SuperPoint 网络包括一组深度卷积层,提取多尺度特征。作者直接将兴趣点网络和一个计算兴趣点描述器的子网络结合起来。图1展示了最终系统的结构。
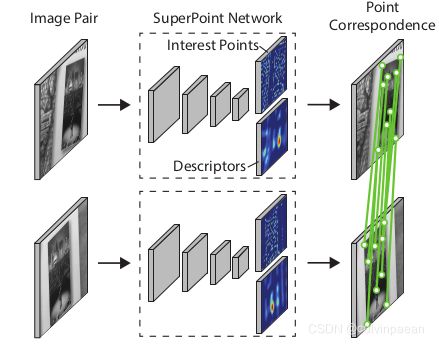
图1. 几何对应的 SuperPoint。作者提出了一个全卷积网络,在单次前向传播中,计算类似于 SIFT 的 2D 兴趣点位置和描述符。在 Titan X GPU 上对 480x640 的图像输入,推理速度是 70 FPS。
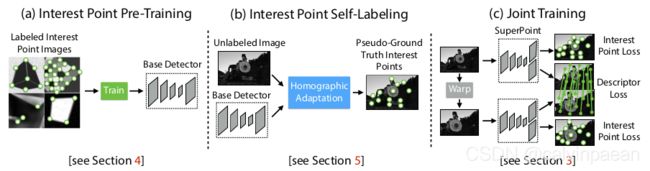
图2. 自监督训练概览。在自监督方法中,作者(a)会在合成数据上预训练一个初版兴趣点检测器,然后(b)通过单应自适应,从目标、未标注的域自动地标注图像。然后用这些生成的标签来训练一个全卷积网络,它能协同地从图像中提取出兴趣点和描述符。
2. Related Work
传统的兴趣点检测器都有了详尽的评测。FAST 角点检测器是第一个用机器学习来解决快速角点检测的系统,SIFT 可能是计算机视觉领域中最有名的、传统的局部特征描述方法。
SuperPoint 架构受到了最近一些进展的启发,将深度学习应用到兴趣点检测和描述符学习上。在匹配图像的子结构上,本文方法和 UCN 和 DeepDesc 相似;但是,这两个都不是做兴趣点检测的。另一方面,LIFT 用卷积的方式替代 SIFT,和传统的基于图像块先检测再描述的方式接近。LIFT 包括兴趣点检测、朝向预测和描述符计算,但是额外需要一个来自于经典 SfM 系统的监督。表1中列出了这些区别。
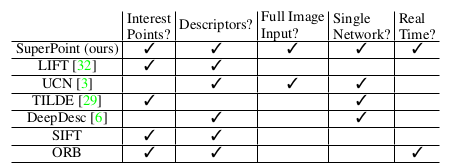
表1. 相关方法的比较。SuperPoint 方法是唯一在单个网络中能实时地计算兴趣点和描述符的方法。
另一个监督领域的极端就是 QuadNetworks,它以非监督的方式来解决兴趣点检测问题;但是该系统是基于图像块的(输入是小图像块),网络较浅,只有2层。TILDE 兴趣点检测系统使用了和单应自适应相似的原理,但是该方法没有从大型全卷积网络中得到帮助。
本文方法也可和其他自监督方法、合成-真实域自适应方法相比。等价landmark变换与单应自适应相近,由 Honari 等人提出。几何匹配网络和深度图像单应预测使用了一个相似的自监督策略,构建训练数据来预测全局变换。但是这些方法都没有用于生成兴趣点和点对应关系,而更高层级的计算机视觉任务如 SLAM 和 SfM 是需要的。协同的姿态和深度估计模型也有人提出,但是没有用到兴趣点。
3. SuperPoint 结构
作者设计了一个全卷积网络 SuperPoint,输入是全尺寸的图像,单次前向计算就可得到兴趣点检测和长度固定的描述符(如图3)。模型有一个共享的编码器来处理、降低输入图像的维度。之后,网络会分成两个解码器 heads,学习各自的权重 — 一个用于兴趣点预测,一个用于兴趣点的描述。网络大部分的参数会在这两个任务之间共享,而传统的方法是首先检出兴趣点,然后计算描述符,无法在两个任务间共享计算和表征。

图3. SuperPoint 解码器。这两个解码器的输入是共享的,其表征的空间分辨率降低了。为了让模型训练起来更迅速、简洁,解码器使用了上采样来将表征大小恢复回 R H × W \mathbb{R}^{H\times W} RH×W。
3.1 共享编码器
SuperPoint 使用了一个 VGG 风格的编码器来降低图像的维度。编码器包括卷积层、空间下采样(池化)和非线性激活。编码器使用了三个最大池化层,对于大小是 H × W H\times W H×W的图像,我们定义 H c = H / 8 H_c=H/8 Hc=H/8, W c = W / 8 W_c=W/8 Wc=W/8。作者将低维度输出的像素点称作“cells”,通过编码器中三个 2 × 2 2\times 2 2×2的非重叠最大池化操作,我们可以得到 8 × 8 8\times 8 8×8的像素cells。编码器将输入图像 I ∈ R H c × W c × F I\in \mathbb{R}^{H_c\times W_c\times F} I∈RHc×Wc×F映射为一个中间张量 B ∈ R H c × W c × F \mathcal{B}\in \mathbb{R}^{H_c\times W_c\times F} B∈RHc×Wc×F,其空间维度更小、通道深度更深(即 H c < H , W c < W , F > 1 H_c < H, W_c
3.2 兴趣点编码器
对于兴趣点检测,输出的每个像素点都对应着一个“point-ness”概率。密集预测任务的一般网络设计都会包含一对编码器-解码器,通过池化或 strided conv 降低空间分辨率,然后通过上采样恢复到原来的分辨率,SegNet 就是这么做的。然而上采样会增大计算量,因此作者设计了具备解码器功能的兴趣点检测 head,降低模型计算量,该解码器没有参数,在 TensorFlow 中叫做“subpixel conv”或“depth to space”,在 PyTorch中叫做"pixel shuffle"。
兴趣点检测 head 对 X ∈ R H c × W c × 65 \mathcal{X}\in \mathbb{R}^{H_c\times W_c\times 65} X∈RHc×Wc×65做计算,输出张量的大小是 R H × W \mathbb{R}^{H\times W} RH×W。65个通道对应着局部、非重叠的 8 × 8 8\times 8 8×8个像素网格区域,以及一个额外的“无兴趣点”的dustbin选项。通过通道 softmax,dustbin 维度会被去除,会进行 R H c × W c × 64 ⇒ R H × W \mathbb{R}^{H_c\times W_c\times 64} \Rightarrow \mathbb{R}^{H\times W} RHc×Wc×64⇒RH×W变形操作。
3.3 描述器解码器
描述器 head 计算 D ∈ R H c × W c × D \mathcal{D}\in \mathbb{R}^{H_c\times W_c\times D} D∈RHc×Wc×D,输出的张量大小是 R H × W × D \mathbb{R}^{H\times W\times D} RH×W×D。为了得到 dense map(该 map 由 L2-归一化、固定长度的描述符组成),作者使用了一个与 UCN 相似的模型,首先输出描述符的半密集的网格(即每8个像素点输出1个)。半密集地学习描述符可以降低训练内存使用,保持运行效率。然后解码器对描述符进行双三次插值,然后通过 L2-归一化将激活值变为单位长度。图3中介绍了该描述符解码器。
3.4 损失函数
损失函数是两个中间损失的和:一个用于兴趣点预测 L p \mathcal{L}_p Lp,一个用于描述符 L d \mathcal{L}_d Ld。作者使用一对合成的变形图像,它们都有 (a) 伪 ground-truth 兴趣点位置和 (b) 根据随机生成的单应矩阵 H \mathcal{H} H 得到的 ground-truth 对应位置,这就可将两张图片联系起来。这样就可同时优化这两项损失,如图2c所示。我们使用 λ \lambda λ来平衡最终的损失:
L ( X , X ′ , D , D ′ ; Y , Y ′ , S ) = L p ( X , Y ) + L p ( X ′ , Y ′ ) + λ L d ( D , D ′ , S ) (1) \mathcal{L}(\mathcal{X}, \mathcal{X'}, \mathcal{D}, \mathcal{D'}; Y, Y', S) = \mathcal{L}_p(\mathcal{X},Y) + \mathcal{L}_p(\mathcal{X'}, Y') + \lambda \mathcal{L}_d(\mathcal{D}, \mathcal{D'}, S) \tag{1} L(X,X′,D,D′;Y,Y′,S)=Lp(X,Y)+Lp(X′,Y′)+λLd(D,D′,S)(1)
兴趣点检测损失函数 L p \mathcal{L}_p Lp是一个对所有cells x h w ∈ X x_{hw}\in\mathcal{X} xhw∈X的全卷积交叉熵损失。将对应的ground-truth 兴趣点标签集合用 Y Y Y表示,单个标记为 y h w y_{hw} yhw。损失是:
L p ( X , Y ) = 1 H c W c ∑ h = 1 , w = 1 H c , W c l p ( x h w ; y h w ) (2) \mathcal{L}_p(\mathcal{X},Y)=\frac{1}{H_c W_c} \sum_{h=1,w=1}^{H_c,W_c} l_p(\mathbf{x}_{hw};y_{hw}) \tag{2} Lp(X,Y)=HcWc1h=1,w=1∑Hc,Wclp(xhw;yhw)(2)
其中,
l p ( x h w ; y ) = − log ( exp ( x h w y ) ∑ k = 1 65 exp ( x h w k ) ) (3) l_p(\mathbf{x}_{hw};y) = -\log (\frac{\exp(\mathbf{x}_{hwy})}{\sum_{k=1}^{65} \exp(\mathbf{x}_{hwk})}) \tag{3} lp(xhw;y)=−log(∑k=165exp(xhwk)exp(xhwy))(3)
描述符损失用在所有成对的描述符 cells 上, d h w ∈ D \mathbf{d}_{hw}\in \mathcal{D} dhw∈D 来自于第一张图片, d h ′ w ′ ′ ∈ D ′ \mathbf{d}'_{h'w'}\in \mathcal{D'} dh′w′′∈D′ 来自于第二张图片。 ( h , w ) (h,w) (h,w) cell 和 ( h ′ , w ′ ) (h',w') (h′,w′) cell 之间的单应性关系可以写作:
s ( h w h ′ w ′ ) = { 1 , if ∥ H p h w ^ − p h ′ w ′ ∥ ≤ 8 0 , otherwise (4) s(hwh'w')=\left\{ \begin{aligned} 1 & , & \text{if} \left \| \widehat{\mathcal{H}\textbf{p}_{hw}}-\textbf{p}_{h'w'} \right \| \leq 8\\ 0 & , & \text{otherwise} \end{aligned} \right. \tag{4} s(hwh′w′)=⎩⎨⎧10,,if∥∥∥Hphw −ph′w′∥∥∥≤8otherwise(4)
其中 p h w \textbf{p}_{hw} phw表示 ( h , w ) (h,w) (h,w) cell 中心像素点的坐标, H p h w ^ \widehat{\mathcal{H}\textbf{p}_{hw}} Hphw 表示将cell位置 p h w \textbf{p}_{hw} phw和单应矩阵 H \mathcal{H} H相乘,再除以最后一个坐标,这在欧氏距离和齐次坐标转换时经常用到。我们将一对图像中所有的对应关系集合标记为 S S S。
作者也增加了一个加权项 λ d \lambda_d λd,平衡正负对应关系的作用(负对应关系要远多于正对应关系)。作者使用了 hingle 损失,positive margin 为 m p m_p mp,negative margin 为 m n m_n mn。描述器损失的定义是:
L d ( D , D ′ , S ) = 1 ( H c W c ) 2 ∑ h = 1 , w = 1 H c , W c ∑ h ′ = 1 , w ′ = 1 H c , W c l d ( d h w , d ′ h ′ w ′ ; s h w h ′ w ′ ) (5) \mathcal{L}_d(\mathcal{D},\mathcal{D'},S)=\frac{1}{(H_cW_c)^2}\sum_{h=1,w=1}^{H_c,W_c} \sum_{h'=1,w'=1}^{H_c,W_c} l_d(\mathbf{d}_{hw}, \mathbf{d'}_{h'w'};s_{hwh'w'}) \tag{5} Ld(D,D′,S)=(HcWc)21h=1,w=1∑Hc,Wch′=1,w′=1∑Hc,Wcld(dhw,d′h′w′;shwh′w′)(5)
其中
l d ( d , d ′ ; s ) = λ d ∗ s ∗ max ( 0 , m p − d T d ′ ) + ( 1 − s ) ∗ max ( 0 , d T d ′ − m n ) (6) l_d(\mathbf{d},\mathbf{d'};s)=\lambda_d \ast s\ast \max(0, m_p-\mathbf{d}^T\mathbf{d'}) + (1-s)\ast\max(0, \mathbf{d}^T\mathbf{d'}-m_n) \tag{6} ld(d,d′;s)=λd∗s∗max(0,mp−dTd′)+(1−s)∗max(0,dTd′−mn)(6)
4. 合成数据预训练
作者介绍了训练一个基线模型的方法(如图2a),叫做 MagicPoint,以自监督的方式,使用单应自适应方法给未标注的图片生成伪ground-truth兴趣点标签。
4.1 Synthetic Shapes
目前市面上没有兴趣点标注图像数据集。所以为了训练兴趣点检测器,作者构建了一个大规模合成数据集,叫做Synthetic Shapes,它由简单的 2D 几何形状组成,如平行四边形、三角形、线条和椭圆。图4中展示了一些例子。在该数据集中,我们可以通过对 Y-连接、L-连接、T-连接、小椭圆的中心点和线段的端点建模来去除模糊的标签。
当合成图片渲染完成后,我们对每张图片使用单应性扭曲来增加训练样本。数据生成得非常快,而且不会出现重复图片。尽管Synthetic Shapes 的兴趣点种类只涉及了真实世界中潜在兴趣点的一部分,但作者发现在实际操作中,它训练出的兴趣点检测器表现是非常不错的。

图4. 合成预训练。Synthetic Shapes数据集包含了三角形、平行四边形、线条、立方体、棋盘形状和星形,每个都有ground-truth角点位置。该数据集用于训练 MagicPoint CNN,和传统检测器相比,它对噪点更加鲁棒。
4.2 MagicPoint
作者将 SuperPoint 的检测器在Synthetic Shapes上训练。将该模型称作 MagicPoint。
当作者将 MagicPoint 和其它传统的角点检测方法如 FAST、Harris 角点和 Shi-Tomasi 的 “Good Features To Track” 一起在 Synthetic Shapes 上比较时,作者发现 MagicPoint 有一定的优势。在表2中,作者报告了在 Synthetic Shapes 数据集上的 mAP。传统的检测器对于有噪声的图像是比较困难的,图4展示了一些例子。

表2. 在 Synthetic Shapes 上检测器的表现。MagicPoint 模型对简单的几何形状的角点检测,是领先于其它传统的检测器的,而且对于噪声更加鲁棒。
MagicPoint 检测器在 Synthetic Shapes 上表现不错,那是否能泛化到真实的图像上呢?作者的回答是可以,但不像我们所期待的那样。作者发现,MagicPoint 能够在真实世界的图像上表现可以,尤其是图像中包含很明显角点的形状,比如桌子、椅子和窗户。但对于自然图像,当视角发生改变时,它的表现就会不如经典的检测器。这就促使作者提出了自监督方法,它在真实世界的图像上训练模型,将之称作单应自适应方法。
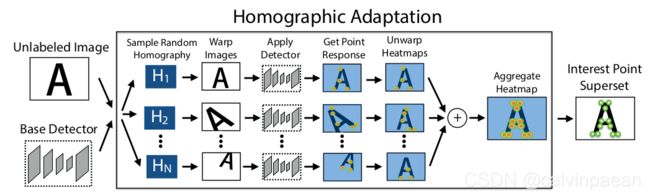
图5. 单应自适应。单应自适应是一种自监督方法,提升兴趣点检测器的几何相容性。整个流程都定义在了等式10中。
5. Homographic Adaptation
本系统开始时用到了一个基础的兴趣点检测器,以及目标空间的大规模未标注图像集(如 MS-COCO)。通过自监督的方式,首先产生目标空间中,每张图片的伪 ground-truth 兴趣点坐标集合,然后使用传统的监督学习机制。本方法的核心过程就是,对输入图像使用随机单应性变换,产生变形版本,再将结果组合起来—作者将该过程叫做单应自适应(图5)。
5.1 Formulation
对于相机运动(相机中心点旋转)、目标距离较大的场景和平面场景,单应矩阵能给出近乎准确的图像到图像的变换关系。因为大多数的世界都是平面的,我们从不同的角度看向同一个三维点时,就可以使用单应性。因为单应性不需要三维信息,它们可以随机选取,很容易就可用到二维图像上—这只涉及到一些双线性插值。因此,单应矩阵是本文自监督方法的核心。
用 f θ ( ⋅ ) f_{\theta}(\cdot) fθ(⋅)表示初始的兴趣点函数, I I I是输入图像, x \mathbf{x} x是兴趣点, H \mathcal{H} H是随机单应性。这样:
x = f θ ( I ) (7) \mathbf{x}=f_{\theta}(I)\tag{7} x=fθ(I)(7)
一个理想的兴趣点算子应该与单应矩阵是共变的。函数 f θ ( ⋅ ) f_{\theta}(\cdot) fθ(⋅)与 H \mathcal{H} H是共变的,如果输出对输入做变换。换句话说,对于所有的 H \mathcal{H} H,一个共变检测器满足:
H x = f θ ( H ( I ) ) (8) \mathcal{H}\mathbf{x}=f_\theta (\mathcal{H}(I)) \tag{8} Hx=fθ(H(I))(8)
将与单应矩阵相关的项移到右边,得到:
x = H − 1 f θ ( H ( I ) ) (9) \mathbf{x}=\mathcal{H}^{-1}f_{\theta}(\mathcal{H}(I)) \tag{9} x=H−1fθ(H(I))(9)
实际操作中,检测器不会完全共变—不同的单应矩阵会产生不同的兴趣点 x \mathbf{x} x。单应自适应背后的思想就是,对大量随机产生的 H \mathcal{H} H做试验性求和(看图5)。这些和可以带来一个全新、改进的 super-point 检测器, F ^ ( ⋅ ) \hat F(\cdot) F^(⋅):
F ^ ( I ; f θ ) = 1 N h ∑ i = 1 N h H i − 1 f θ ( H i ( I ) ) (10) \hat F(I; f_{\theta}) = \frac{1}{N_h} \sum_{i=1}^{N_h} \mathcal{H}_i^{-1} f_\theta (\mathcal{H}_i(I)) \tag{10} F^(I;fθ)=Nh1i=1∑NhHi−1fθ(Hi(I))(10)
5.2 Choosing Homographies
不是所有的 3 × 3 3\times 3 3×3矩阵都适合做单应自适应。为了找到合适的单应矩阵,适合进行相机变换,作者将一个可能的单应矩阵拆成多个简单的变换类别。在提前设好的范围内,通过截断的正态分布在平移、缩放、平面内旋转和对称透视扭曲之间做选择。进行中心点区域裁剪是为了避免边缘噪声的影响。图6展示了这个过程。
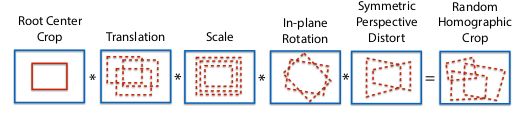
图6. 随机单应生成。作者将简单的变换组合起来,生成随机的单应矩阵。
对输入图像做单应自适应时,我们对它的多个单应变形响应值取平均。单应变形的个数 N h N_h Nh是个超参数。在实验中, N h = 1 N_h=1 Nh=1表示没有做单应自适应。作者通过实验来寻找 N h N_h Nh 最合适的值, N h N_h Nh的取值范围在10到100,1000之间。实验表明,当 N h N_h Nh超过100时,返回结果会退化。在 MS-COCO 图像上,没有用任何的单应自适应时,作者取得了0.67的再现得分,当 N h = 100 N_h=100 Nh=100时,取得了 21 % 21\% 21%的提升,当 N h = 1000 N_h=1000 Nh=1000时,再现得分提升了 22 % 22\% 22%。因此,当 N h > 100 N_h>100 Nh>100时,得到的提升是有限的。在附录C中,作者进行了详细的分析和讨论。
5.3 Iterative Homographic Adaptation
训练时,作者使用了单应自适应来提升基础模型 MagicPoint 在真实图像上的泛化性。该过程可以迭代进行,持续地自监督,从而提升兴趣点检测器的性能。在所有的实验中,作者将这个模型称作 SuperPoint,在图7中展示了这类效果。

图7. 迭代的单应自适应。上面一层:初始基线检测器(MagicPoint)尝试找到可重复的兴趣点。中间和下面一层:使用单应自适应进一步训练后的效果提升。
6. 实验细节
这一部分针对 MagicPoint 和 SuperPoint 模型的训练,作者提供了一些实现细节。编码器的结构类似于 VGG,有8个 3 × 3 3\times 3 3×3卷积层,大小分别是64-64-64-64-128-128-128-128。每两层都有一个 2 × 2 2\times 2 2×2的最大池化层。每个解码器都有一个 3 × 3 3\times 3 3×3卷积层,有256个单元,后面有一个 1 × 1 1\times 1 1×1卷积层,对于兴趣点检测有65个单元,对于描述器有256个单元。所有的卷积层后面都有 ReLU 非线性激活和 BatchNorm 归一化。
为了训练全卷积 SuperPoint 模型,作者开始时在 Synthetic Shapes 上训练 MagicPoint 模型。MagicPoint 就是不带描述器head的 SuperPoint。MagicPoint 在合成数据上训练了20万次迭代。因为渲染合成数据简单、快速,网络不会输入两个一样的样本。
作者使用 MagicPoint 基础检测器和 MS-COCO 2014 来生成伪ground-truth 标签,它大约有8万张图片。图像会被缩放到 240 × 320 240\times 320 240×320的分辨率,转为灰度图。然后用单应自适应来生成标签, N h = 100 N_h=100 Nh=100。然后使用第一轮训练的单应自适应模型,再进行一次单应自适应。
SuperPoint 的协同训练也是在 240 × 320 240\times 320 240×320分辨率的灰度图上完成的。对于每个训练样本,会随机选择一个单应矩阵。这次选择的单应矩阵集合要比单应自适应时更加严格,为了更好地建模目标之间的配对(比如,我们没有选择极端的平面内旋转情形,因为它们在 HPatches 中很少见)。图像和对应的伪ground-truth 标签会利用该单应进行变换,生成出想要的输入和标签。描述符的大小定为 D = 256 D=256 D=256。作者使用了一个加权项 λ d = 250 \lambda_d=250 λd=250,保证描述器学习是均衡的。描述器的 hinge loss 使用了一个 positive margin m p = 1 m_p=1 mp=1,negative margin 为 m n = 0.2 m_n=0.2 mn=0.2。作者使用了 λ = 0.0001 \lambda=0.0001 λ=0.0001 来平衡这两个损失。
训练都是用 PyTorch 完成的,mini-batch 大小是32,使用了ADAM solver,学习率默认为0.001, β = ( 0.9 , 0.999 ) \beta=(0.9, 0.999) β=(0.9,0.999)。作者也使用了标准的数据增广如随机高斯噪声、运动模糊、亮度层级调节,提升网络对亮度和视角变化的鲁棒性。
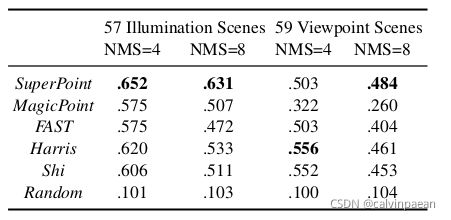
表3. HPatches 检测器的再现性。SuperPoint 对于光照变化和视角变化,是再现性最高的算法,全方面领先于 MagicPoint。
Appendix
A. Evaluation Metrics
这一部分,作者介绍了更多关于评价尺度的细节。因为本文的全卷积模型没使用局部图块,作者就没计算图块的重叠度,而是通过计算2D检测中心点的距离来比较检测距离。对于多尺度方法如SIFT和ORB,作者比较了最高分辨率层级的距离。
角点检测平均精度。作者计算了精度-召回曲线以及相应的AUC(即平均精度),正确检测结果的像素位置错误率,以及再现率。对于角点检测,本文使用了一个阈值 ϵ \epsilon ϵ,判断返回的点位置 x \mathbf{x} x是正确的,对于一组 K K K个 ground-truth 角点 { x ^ 1 , . . . , x ^ K } \{\hat \mathbf{x}_1, ..., \hat \mathbf{x}_K\} {x^1,...,x^K}来说。作者定义正确的检测结果的依据是:
Corr ( x ) = ( min j ∥ x − x ^ j ∥ ) ≤ ϵ . (11) \text{Corr}(\mathbf{x}) = (\min_j \left \| \mathbf{x} - \hat \mathbf{x}_j \right \|) \leq \epsilon. \tag{11} Corr(x)=(jmin∥x−x^j∥)≤ϵ.(11)
通过改变检测置信度,我们可以得到一个精度召回曲线,即平均精度(取值范围是0到1之间),AP越大越好。
定位错误率。为了补充AP分析,作者计算了角点检测错误率,但只针对正确的检测结果。定位错误率定义如下:
LE = 1 N ∑ i : Corr ( x i ) min j ∈ { 1 , . . . , K } ∥ x i − x ^ j ∥ (12) \text{LE} = \frac{1}{N} \sum_{i:\text{Corr}(\mathbf{x}_i)} \min_{j\in \{1,...,K\}} \left \| \mathbf{x}_i - \hat \mathbf{x}_j \right \| \tag{12} LE=N1i:Corr(xi)∑j∈{1,...,K}min∥xi−x^j∥(12)
定位错误率在0和 ϵ \epsilon ϵ之间,LE越低越好。
再现率。作者计算了两张图片的兴趣点检测器的再现率。因为 SuperPoint 结构是全卷积的,没有提取图像块,我们就无法计算图像块重叠度,但我们可以计算 2D 点中心的距离,从而计算再现率。作者使用 ϵ \epsilon ϵ表示两个点之间正确的距离阈值。我们假设第一张图片中有 N 1 N_1 N1个点,第二张图片中有 N 2 N_2 N2个点。再现率的定义如下:
Corr ( x i ) = ( min j ∈ { 1 , . . . , N 2 } ∥ x i − x ^ j ∥ ) ≤ ϵ (13) \text{Corr}(\mathbf{x}_i) = (\min_{j\in \{1,...,N_2\}} \left \| \mathbf{x}_i - \hat \mathbf{x}_j\right \|) \leq \epsilon \tag{13} Corr(xi)=(j∈{1,...,N2}min∥xi−x^j∥)≤ϵ(13)
再现率计算的是,在第二张图片中检测出某点的概率。
Rep = 1 N 1 + N 2 ( ∑ i Corr ( x i ) + ∑ j Corr ( x j ) ) (14) \text{Rep} = \frac{1}{N_1 + N_2} (\sum_i \text{Corr}(\mathbf{x}_i) + \sum_j \text{Corr}(\mathbf{x}_j)) \tag{14} Rep=N1+N21(i∑Corr(xi)+j∑Corr(xj))(14)
Nearest Neighbor mean Average Precision。该指标通过多个描述符的距离阈值来评估描述符的差异程度。它是通过精度-召回曲线来计算出AUC,使用最近邻匹配策略。对所有的图像对计算该指标,求其均值。
Matching score。该指标计算兴趣点检测器和描述符的整体表现。它计算重叠的视角区域内 ground-truth 对应关系的比率。对所有的图像对计算该指标,求其均值。
单应矩阵预测。通过比较预测的单应矩阵 H ^ \hat \mathcal{H} H^和ground-truth 单应矩阵 H \mathcal{H} H,作者计算了算法预测一对图片单应矩阵的能力。直接比较 3 × 3 3\times 3 3×3的单应矩阵 H \mathcal{H} H并不容易,因为矩阵中数字都有不同的尺度。作者比较了单应矩阵是如何将一张图片的四个角点变换为其它点的。将第一张图片的四个角点定义为 c 1 , c 2 , c 3 , c 4 \mathbf{c}_1, \mathbf{c}_2, \mathbf{c}_3, \mathbf{c}_4 c1,c2,c3,c4。然后对第二张图片使用ground-truth H \mathcal{H} H 来得到其ground-truth角点, c ′ 1 , c ′ 2 , c ′ 3 , c ′ 4 \mathbf{c'}_1, \mathbf{c'}_2, \mathbf{c'}_3, \mathbf{c'}_4 c′1,c′2,c′3,c′4,用预测的单应矩阵 H ^ \hat \mathcal{H} H^得到 c ′ ^ 1 , c ′ ^ 2 , c ′ ^ 3 , c ′ ^ 4 \hat \mathbf{c'}_1, \hat \mathbf{c'}_2, \hat \mathbf{c'}_3, \hat \mathbf{c'}_4 c′^1,c′^2,c′^3,c′^4。我们用一个阈值 ϵ \epsilon ϵ来表示正确的单应矩阵。
CorrH = 1 N ∑ i = 1 N ( ( 1 4 ∑ j = 1 4 ∥ c ′ i j − c ^ i j ∥ ) ≤ ϵ ) (15) \text{CorrH} = \frac{1}{N}\sum_{i=1}^N \left( \left( \frac{1}{4} \sum_{j=1}^4 \left \| \mathbf{c'}_{ij} - \hat \mathbf{c}_{ij} \right \| \right) \leq \epsilon \right) \tag{15} CorrH=N1i=1∑N((41j=1∑4∥c′ij−c^ij∥)≤ϵ)(15)
取值范围在0到1之间,越高越好。