基于CHNN求解TSP问题
目录
- 基于CHNN求解TSP问题
-
- CHNN
-
- CHNN的网络结构
- CHNN状态方程
- CHNN的能量函数
- TSP问题
- 基于CHNN求解TSP问题的思路
-
- 1. 分析问题,将TSP的状态用数学符号描述出来
-
- 1.1 TSP问题描述
- 1.2 TSP问题的约束条件
- 1.3 TSP问题的目标函数
- 2. 构造网络能量函数
- 3. 优化网络能量函数
- 4. CHNN的动态方程
- 5. 状态更新方程
- python代码实现
基于CHNN求解TSP问题
CHNN
CHNN是连续型Hopfield神经网络。CHNN是以模拟量作为网络的输入和输出,而且各个神经元之间的工作方式是并行的。因此相对于DHNN,CHNN更接近于生物神经网络。CHNN更适合于求解组合优化问题。
CHNN的网络结构
CHNN的神经网络结构可以等效为放大电子电路。每一个神经元可以等效为一个电路放大器元件。CHNN的等效电路拓扑图如下:
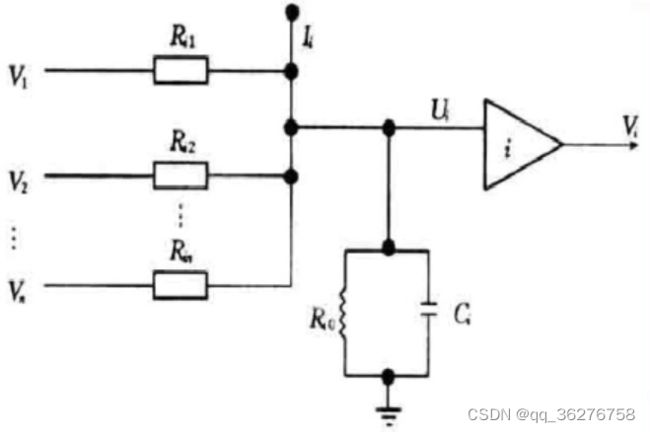
其中:
U i U_i Ui 是放大电子元件的输入电压,对应于CHNN神经网络中神经元的输入,包括恒定的外部电流和其他电子元件的反馈连接。
V i V_i Vi是放大电子元件的输出电压,对应于CHNN神经网络中神经元的输出,其输出有正负值,正值代表兴奋,负值代表抑制。
运算放大器 i i i表示第 i i i个神经元。
CHNN状态方程
设电容C的两端电压为 U c U_c Uc,存储的电荷量为Q,则有 C = Q U c C=\frac{Q}{U_c} C=UcQ
则经过电容C的电流为: i = d Q d t = C d U c d t i = \frac{dQ}{dt}=C\frac{dU_c}{dt} i=dtdQ=CdtdUc
根据基尔霍夫电流定律,CHNN等效电路的电流关系为:
C i d u i d t + u i R i 0 = ∑ j = 1 n 1 R i j ( v j − u i ) + I i C_i\frac{du_i}{dt}+\frac{u_i}{R_{i0}}=\sum_{j=1}^{n}\frac{1}{R_{ij}}(v_j-u_i)+I_i Cidtdui+Ri0ui=j=1∑nRij1(vj−ui)+Ii
令 T i j T_{ij} Tij表示神经网络中神经元之间的连接权重: T i j = 1 R i j T_{ij}=\frac{1}{R_{ij}} Tij=Rij1
则电流关系式可以化简为
C i d u i d t = ∑ j = 1 n T i j ( v j − u i ) + I i − T i 0 u i ⇒ C i d u i d t = ∑ j = 1 n T i j v j + I i − T i u i C_i\frac{du_i}{dt}=\sum_{j=1}^{n}T_{ij}(v_j-u_i)+I_i-T_{i0}u_i \\ \Rightarrow C_i\frac{du_i}{dt}=\sum_{j=1}^{n}T_{ij}v_j+I_i-T_{i}u_i Cidtdui=j=1∑nTij(vj−ui)+Ii−Ti0ui⇒Cidtdui=j=1∑nTijvj+Ii−Tiui
上式就是CHNN神经网络的状态方程,其中 v i = f i ( u i ) v_i=f_i(u_i) vi=fi(ui),即输入电压是输出电压的非线性映射。 f i f_i fi是S型激励函数
CHNN的能量函数
由于CHNN的神经网络模型中的权重是不变的,并且不需要学习,因此我们采用能量函数的方式来衡量网路的稳定性。
CHNN网络能量函数公式如下:
E = − 1 2 ∑ i = 1 n ∑ j = 1 n T i j v i v j − ∑ i = 1 n v i I i + ∑ i = 1 n 1 R i ∫ 0 u i f − 1 ( v i ) d v i E=-\frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}T_{ij}v_iv_j-\sum_{i=1}^{n}v_iI_i+\sum_{i=1}^{n}\frac{1}{R_i}\int_0^{u_i}f^{-1}(v_i)dv_i E=−21i=1∑nj=1∑nTijvivj−i=1∑nviIi+i=1∑nRi1∫0uif−1(vi)dvi
TSP问题
旅行商(TSP)问题是人工智能领域一个组合优化问题。
问题描述:有一个推销员,要到n个城市推销商品,他要找出一个包含所有n个城市的具有最短路程的环路。
基于CHNN求解TSP问题的思路
1. 分析问题,将TSP的状态用数学符号描述出来
1.1 TSP问题描述
我们假设一共有5个城市,A、B、C、D、E。我们使用一个 5 × 5 5\times5 5×5矩阵表示每一种走法(状态)。
| 城市 | 第一步 | 第二步 | 第三步 | 第四步 | 第五步 |
|---|---|---|---|---|---|
| A | 0 | 0 | 1 | 0 | 0 |
| B | 1 | 0 | 0 | 0 | 0 |
| C | 0 | 1 | 0 | 0 | 0 |
| D | 0 | 0 | 0 | 1 | 0 |
| E | 0 | 0 | 0 | 0 | 1 |
如上表所示, v x i = 1 v_{xi}=1 vxi=1 表示第i步在第x城市, v x i = 0 v_{xi}=0 vxi=0 表示第i步不在第x城市 。
故,每个元素的取值为0或1
注:x,y表示城市,i,j表示的第几步
1.2 TSP问题的约束条件
TSP问题有三个约束条件
-
一个城市只去一次 =====> 每一行只有一个‘1’
第 x 行 的 所 有 元 素 V x i 按 顺 序 两 两 相 乘 之 和 为 0 ∑ i = 1 n − 1 ∑ j = i + 1 n V x i V x j = 0 第x行的所有元素V_{xi}按顺序两两相乘之和为0 \\ \sum_{i=1}^{n-1}\sum_{j=i+1}^{n}V_{x_i}V_{x_j} = 0 第x行的所有元素Vxi按顺序两两相乘之和为0i=1∑n−1j=i+1∑nVxiVxj=0

那 么 所 有 行 的 所 有 元 素 V x i 按 顺 序 两 两 相 乘 之 和 为 0 ∑ x = 1 n ∑ i = 1 n − 1 ∑ j = i + 1 n V x i V x j = 0 那么所有行的所有元素V_{xi}按顺序两两相乘之和为0 \\ \sum_{x=1}^{n}\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}V_{x_i}V_{x_j} = 0 那么所有行的所有元素Vxi按顺序两两相乘之和为0x=1∑ni=1∑n−1j=i+1∑nVxiVxj=0 -
一次只去一个城市 =====> 每一列只有一个‘1’
第 i 列 的 所 有 元 素 V x i 按 顺 序 两 两 相 乘 之 和 为 0 ∑ x = 1 n − 1 ∑ y = x + 1 n V x i V y i = 0 第i列的所有元素V_{xi}按顺序两两相乘之和为0 \\ \sum_{x=1}^{n-1}\sum_{y=x+1}^{n}V_{x_i}V_{y_i} = 0 第i列的所有元素Vxi按顺序两两相乘之和为0x=1∑n−1y=x+1∑nVxiVyi=0
那 么 所 有 列 的 所 有 元 素 V x i 按 顺 序 两 两 相 乘 之 和 为 0 ∑ i = 1 n ∑ x = 1 n − 1 ∑ y = x + 1 n V x i V y i = 0 那么所有列的所有元素V_{xi}按顺序两两相乘之和为0 \\ \sum_{i=1}^{n}\sum_{x=1}^{n-1}\sum_{y=x+1}^{n}V_{x_i}V_{y_i} = 0 那么所有列的所有元素Vxi按顺序两两相乘之和为0i=1∑nx=1∑n−1y=x+1∑nVxiVyi=0 -
一共有n个城市 =====> 矩阵之和为n ∑ x = 1 n ∑ i = 1 n V x i = n \sum_{x=1}^{n}\sum_{i=1}^{n}V_{x_i}=n x=1∑ni=1∑nVxi=n
1.3 TSP问题的目标函数
我们想要得到的是访问n个城市的总距离最小。我们使用 d x y d_{xy} dxy表示 x x x与 y y y两个城市的距离,那么顺序访问城市 x x x和城市 y y y,有 d x y V x i V y , i + 1 和 d x y V x i V y , i − 1 d_{xy}V_{xi}V_{y, i+1}和d_{xy}V_{xi}V_{y,i-1} dxyVxiVy,i+1和dxyVxiVy,i−1至少有一个为0。
那么顺序访问 x x x和 y y y的所有可能的路径有
D x y = ∑ i = 1 n ( d x y V x i V y , i + 1 + d x y V x i V y , i − 1 ) = ∑ i = 1 n d x y V x i ( V y , i + 1 + V y , i − 1 ) D_{xy}=\sum_{i=1}^{n}(d_{xy}V_{xi}V_{y, i+1}+d_{xy}V_{xi}V_{y,i-1}) \\ =\sum_{i=1}^{n}d_{xy}V_{xi}(V_{y, i+1}+V_{y,i-1}) Dxy=i=1∑n(dxyVxiVy,i+1+dxyVxiVy,i−1)=i=1∑ndxyVxi(Vy,i+1+Vy,i−1)
那么顺序访问所有城市的可能的路径有
D = ∑ x = 1 n ∑ y = 1 n ∑ i = 1 n d x y V x i ( V y , i + 1 + V y , i − 1 ) D=\sum_{x=1}^{n}\sum_{y=1}^{n}\sum_{i=1}^{n}d_{xy}V_{xi}(V_{y, i+1}+V_{y,i-1}) D=x=1∑ny=1∑ni=1∑ndxyVxi(Vy,i+1+Vy,i−1)
我们想要得到总距离最小,即上式取最小值。
2. 构造网络能量函数
现在我们就把求解TSP问题转化为求解有三个约束条件下求解最小值的最优化问题。
我们根据三个约束条件和一个优化目标函数来构造网络能量函数
E = A 2 ∑ x = 1 n ∑ i = 1 n − 1 ∑ j = i + 1 n V x i V x i + B 2 ∑ i = 1 n ∑ x = 1 n − 1 ∑ y = x + 1 n V x i V y i + C 2 ( ∑ x = 1 n ∑ i = 1 n V x i − n ) 2 + D 2 ∑ x = 1 n ∑ y = 1 n ∑ i = 1 n d x y V x i ( V y , i + 1 + V y , i − 1 ) E=\frac{A}{2}\sum_{x=1}^{n}\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}V_{x_i}V_{x_i} \\ +\frac{B}{2} \sum_{i=1}^{n}\sum_{x=1}^{n-1}\sum_{y=x+1}^{n}V_{x_i}V_{y_i} \\ +\frac{C}{2}(\sum_{x=1}^{n}\sum_{i=1}^{n}V_{x_i}-n)^2 \\ +\frac{D}{2}\sum_{x=1}^{n}\sum_{y=1}^{n}\sum_{i=1}^{n}d_{xy}V_{xi}(V_{y, i+1}+V_{y,i-1}) E=2Ax=1∑ni=1∑n−1j=i+1∑nVxiVxi+2Bi=1∑nx=1∑n−1y=x+1∑nVxiVyi+2C(x=1∑ni=1∑nVxi−n)2+2Dx=1∑ny=1∑ni=1∑ndxyVxi(Vy,i+1+Vy,i−1)
其中A、B、C、D是常数。
当E达到最小值的时候,就选择了最优路径。
3. 优化网络能量函数
在’Theories on the Hopfield neural networks’这篇论文中对上式进行了改进,提高了收敛速度。改进后的公式如下:
E = A 2 ∑ x = 1 n ( ∑ i = 1 n V x i − 1 ) 2 + A 2 ∑ i = 1 n ( ∑ x = 1 n V x i − 1 ) 2 + D 2 ∑ x = 1 n ∑ y = 1 n ∑ i = 1 n V x i d x y V y , i + 1 E=\frac{A}{2}\sum_{x=1}^{n}(\sum_{i=1}^{n}V_{xi}-1)^2+\frac{A}{2}\sum_{i=1}^{n}(\sum_{x=1}^{n}V_{xi}-1)^2+\frac{D}{2}\sum_{x=1}^{n}\sum_{y=1}^{n}\sum_{i=1}^{n}V_{xi}d_{xy}V_{y, i+1} E=2Ax=1∑n(i=1∑nVxi−1)2+2Ai=1∑n(x=1∑nVxi−1)2+2Dx=1∑ny=1∑ni=1∑nVxidxyVy,i+1
4. CHNN的动态方程
根据优化后的能量函数可以得到动态方程如下:
d U i j d t = − ∂ E ∂ v x i = − A ( ∑ i = 1 n V x i − 1 ) − A ( ∑ x = 1 n V x i − 1 ) − D ∑ y = 1 n d x y v y , i + 1 \frac{dU_{ij}}{dt}=-\frac{\partial E}{\partial v_{xi}}=-A(\sum_{i=1}^{n}V_{xi}-1)-A(\sum_{x=1}^{n}V_{xi}-1)-D\sum_{y=1}^{n}d_{xy}v_{y,i+1} dtdUij=−∂vxi∂E=−A(i=1∑nVxi−1)−A(x=1∑nVxi−1)−Dy=1∑ndxyvy,i+1
5. 状态更新方程
输入状态的更新方程如下:
U i j ( t + 1 ) = U i j ( t ) + d U i j d t Δ t U_{ij}(t+1)=U_{ij}(t)+\frac{dU_{ij}}{dt}\Delta t Uij(t+1)=Uij(t)+dtdUijΔt
输出状态的更新方程为(激活函数使用sigmoid函数):
V i j = 1 2 ( 1 + t a n h ( U i j U 0 ) ) V_{ij}=\frac{1}{2}(1+tanh(\frac{U_{ij}}{U_0})) Vij=21(1+tanh(U0Uij))
python代码实现
下面我们就可以根据以上过程来实现代码
import numpy as np
import random
from math import sqrt, log, tanh, exp
from matplotlib import pyplot as plt
import logging
logging.basicConfig(level=logging.INFO, format='%(asctime)s - %(filename)s[line:%(lineno)d]- %(levelname)s:%(message)s')
# 动态方程中的两个系数
A = 300
D = 200
U0 = 0.1
max_iter = 120 # 最大迭代次数
step = 0.0001 # 步长
def d_u(state_v, distance, n):
""" 动态方程
:param state_v: 输出矩阵
:param distance: 城市之间的距离矩阵
:param n: 城市的个数
:return: 返回 动态方程的矩阵
"""
a = np.sum(state_v, axis=0) - 1 # 得到行向量,把每一列的元素都加到第一行 对前一个下标求和
b = np.sum(state_v, axis=1) - 1 # 得到列向量(列向量的值,行向量的形式),把每一行的元素都加到第一列 对后一个下标求和
# 把上述两个向量扩展为两个矩阵
x = np.array([[0.0 for i in range(n)] for i in range(n)]) # 用来扩展a向量
y = np.array([[0.0 for i in range(n)] for i in range(n)]) # 用来扩展b向量
# 扩展a向量为一个矩阵
for i in range(n):
for j in range(n):
x[i, j] = a[j] # x的每一行都和a向量相同,相当于x矩阵是n行a
# 扩展b向量为一个矩阵
for i in range(n):
for j in range(n):
y[j, i] = b[j] # y的每一列都和b相同,相当于y矩阵是n列b,但是b在python里的形式是行向量
# 创建C矩阵: 将V矩阵的第一列移到最后一列,并与距离矩阵相乘??? 为什么要移动第一列
c = np.array([[0.0 for i in range(n)] for i in range(n)])
c[:, 0:n-1] = state_v[:, 1:n]
c[:, n-1] = state_v[:, 0] # 将V的第一列放到最后一列
c = np.dot(distance, c) # 距离矩阵乘以V
return -A * (x + y) - D * c
def energy(state_v, distance, n):
""" 能量函数
:param state_v: 输出矩阵
:param distance: 距离矩阵
:param n: 城市的个数
:return: 能量函数的值,是一个数
"""
a = sum([x*x for x in (np.sum(state_v, axis=0)-1)])
b = sum([x*x for x in (np.sum(state_v, axis=1)-1)])
c = np.array([[0.0 for i in range(n)] for i in range(n)])
c[:, 0:n-1] = state_v[:, 1:n]
c[:, n-1] = state_v[:, 0] # 将V的第一列放到最后一列
c = np.sum(np.sum(np.multiply(state_v, np.dot(distance, c)), axis=0))
return 0.5 * (A * (a + b) + D * c)
def get_v(state_v, n):
''' 得到稳定状态下的矩阵信息
:param state_v: 稳定输出矩阵
:param n: 城市的个数
:return:
'''
(row, col) = state_v.shape
V_H = np.array([0.0 for i in range(row)]) # 用来存放每一列的最大值,共row行
V_W = np.array([0 for i in range(row)]) # 用来存放每一列最大值的行号
for i in range(n):
for j in range(n):
if V[j, i] > V_H[i]:
V_H[i] = V[j, i]
V_W[i] = j
# 创建一个数组将V中每列最大值的位置设为1,其他设为0
V_1 = np.array([[0 for i in range(row)] for i in range(col)])
for i in range(col):
V_1[V_W[i], i] = 1
return V_H, V_W, V_1
# 归一化处理用到的函数
def normalization(energy_all):
# return [float(x-energy_all.mean())/energy_all.std() for x in energy_all] #z-score
return [log(x)/log(np.max(energy_all)) for x in energy_all] #log函数转化
def draw_enegry(energy_all):
''' 画出能量函数的曲线图
:param energy_all: 能量函数数组
:return: 无返回值
'''
y = normalization(energy_all) # 对能量函数值进行归一化处理
plt.plot(y)
plt.xlabel('迭代次数', loc='right')
plt.ylabel('能量函数值', loc='top')
plt.rcParams['font.sans-serif'] = ['SimHei'] # 中文字体设置-黑体
plt.show()
def draw_rode(state_v, V_1, V_W, n):
''' 画出路线图
:param state_v: 稳定输出矩阵
:param V_1: 0-1状态矩阵
:param V_W: 每列最大值所在的行向量
:param n: 城市个数
:return:
'''
(row, col) = state_v.shape
V_1H = np.array([0.0 for i in range(n)])
V_1W = np.array([0 for i in range(n)])
for i in range(col):
V_1[V_W[i], i] = 1
for i in range(n):
for j in range(n):
if V_1[j, i] > V_1H[i]:
V_1H[i] = V_1[j, i]
V_1W[i] = j
# 随机一种路径和优化后的路径进行比较
city_i = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
V_0W = random.sample(list(city_i), 10)
# 创建两个城市矩阵,将他们按照我们所给的初始顺序和最终顺序进行排序
city_b = np.array(
[[0.0, 0.0], [0.0, 0.0], [0.0, 0.0], [0.0, 0.0], [0.0, 0.0], [0.0, 0.0], [0.0, 0.0], [0.0, 0.0], [0.0, 0.0],
[0.0, 0.0]])
city_f = np.array(
[[0.0, 0.0], [0.0, 0.0], [0.0, 0.0], [0.0, 0.0], [0.0, 0.0], [0.0, 0.0], [0.0, 0.0], [0.0, 0.0], [0.0, 0.0],
[0.0, 0.0]])
k = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
k = [city[i] for i in V_0W]
for i in range(n):
city_b[i] = k[i]
j = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
j = [city[i] for i in V_1W]
for i in range(n):
city_f[i] = j[i]
# 下面将坐标点的X,Y轴数值分别提取进行画图
X_b = []
Y_b = []
X_f = []
Y_f = []
for i in range(n):
X_b.append(city_b[i][0])
Y_b.append(city_b[i][1])
X_f.append(city_f[i][0])
Y_f.append(city_f[i][1])
# 将第一个点加入,因为要回到初始点
X_b.append(city_b[0][0])
Y_b.append(city_b[0][1])
X_f.append(city_f[0][0])
Y_f.append(city_f[0][1])
plt.plot(X_b, Y_b, 'r', X_f, Y_f, '-.b') # 红线是随机,蓝线是优化后的结果
plt.scatter(X_f, Y_f)
plt.legend(labels=['随机路线', '优化后路线'], loc='lower right', fontsize=6) # 图例
plt.rcParams['font.sans-serif'] = ['SimHei'] # 中文字体设置-黑体
plt.show()
if __name__ == '__main__':
city = np.array([
[0.7000, 0.2000], [0.4000, 0.3000], [0.5000, 0.8000],
[0.3000, 0.4000], [0.1000, 0.9000], [0.9000, 0.4000],
[0.8000, 0.6000], [0.6000, 0.9000], [0.3000, 0.6000],
[0.2000, 0.8000]]) # 10个城市的坐标
n = len(city) # 城市的个数
# 计算距离矩阵
distance = np.array([[0.0 for i in range(n)] for i in range(n)])
for i in range(n):
for j in range(n):
a = sqrt((city[i, 0]-city[j, 0]) ** 2 + (city[i, 1]-city[j, 1]) ** 2)
distance[i, j] = a
distance[j, i] = a
# 随机给定网络初始状态矩阵
delta = 2 * (np.random.random((n, n))) - 1 # 随机产生一个n*n的矩阵,用来随机初始化状态矩阵
U = U0 * log(n-1) + delta # 随机定义一个初始输入矩阵
V = np.array([[0.0 for i in range(n)] for i in range(n)])
for i in range(n):
for j in range(n):
# V[i, j] = (1+2/(1+exp(-2*(U[i, j]/U0)))-1)/2
V[i, j] = 0.5 * (1 + tanh(U[i, j] / U0)) # 输出矩阵、状态矩阵
# 创建一个向量,用来存储每一步的能量值
energy_all = np.array([0.0 for i in range(max_iter)])
# 迭代
for k in range(max_iter):
du = d_u(V, distance, n) # 动态方程、梯度
U = U + du * step # 更新输入矩阵
for i in range(n):
for j in range(n):
V[i, j] = 0.5 * (1 + tanh(U[i, j] / U0)) # 输出矩阵、状态矩阵
# V[i, j] = (1 + 2 / (1 + exp(-2 * (U[i, j] / U0))) - 1) / 2
energy_all[k] = energy(V, distance, n) # 求能量函数的值,放入向量中
Vs = get_v(V, n)
draw_enegry(energy_all) # 画出能量函数图
draw_rode(V, V_W=Vs[1], V_1=Vs[2], n=n) # 画出路线图