文献翻译1：Oriented R-CNN for Object Detection

Oriented R-CNN for Object Detection

Xingxing Xie, Gong Cheng, Jiabao Wang, Xiwen Yao, Junwei Han

西北工业大学

ICCV2021

paper: http://arxiv.org/abs/2108.05699

code: https://github.com/jbwang1997/OBBDetection

Abstract

当前的SOTA两阶段检测器生成旋转候选框很费时。本文提出Oriented RCNN(oRPN)，实现具有高效率和良好精度的旋转检测。

具体来说，第一阶段中提出了oRPN，可以几乎不费时地生成oriented proposals；第二阶段oriented RoI。

DOTA: 75.87% mAP

HRSC: 96.50% mAP

Introduction

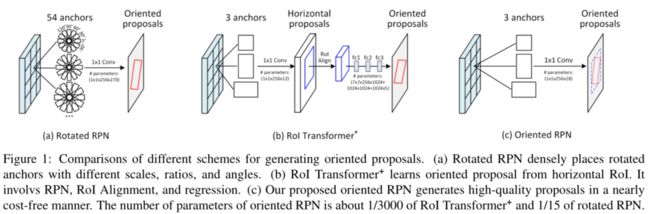
早期的rotated RPN铺3scales × 3ratios × 6 angles个anchor。anchor-based提高了召回率，在稀疏角度有较好表现，但是计算量大、内存占用高。

RoI Transformer为这一问题，从水平RoI中学习OBB，包括RRoR learner、RRoRI wrapper。RoI Transformer大大降低了oriented anchor的数量，降低了计算量和内存占用。但是其资源消耗仍然很大。

作者通过研究发现限制基于区域建议的Oriented Object Detection是第一阶段旋转候选区域提取。因此作者希望设计一个***通用的、简单的旋转候选框提取网络***，因此设计了Oriented RCNN。

1. Oriented RPN(oRPN)是一个轻量的全卷积网络，参数量比oRPN和RoI Trans都少。Oriented RPN通过将RPN的输出由4个改为6个实现。Oriented RPN得益于中点偏移(Midpoint offset)旋转框表示。

2. 第二部分是oriented RCNN detection head(ORH)：从每个oriented proposal中通过rotated RoI alignment提取特征并进行分类和回归。

RoI Align是为解决RoI Pooling中像素映射时坐标取整导致的误差而出现的。

Related Work

由于包含太多背景信息或多个目标，HBB不能紧凑地定位遥感图像中的旋转目标。基于two-stage算法，一个自然的结局方案就是引入OBB，比如oriented RPN。这种方式大大提高了摇杆目标检测的精度。但是由于引入了全连接层和RoI Alignment，这种方式十分复杂。为解决这一问题，有人提出了基于Faster RCNN的SCRDet和Gliding Vertex，用Faster RCNN预测四个顶点的offset。但这两种方法都是用HBB来进行分类，仍然存在特征和目标对不齐的问题。

此外，R3Det等探究了one-stage或者是anchor-free方式的算法。其中R3Det用特征精细化和逐步回归来解决特征对不齐问题。Pan在CenterNet的基础上，设计了一种面向目标的动态精细化网络(DRN)。

与上述方法相比，本文的工作属于proposal-based目标检测方法。作者设计了一种高效的oriented RPN，以突破面向目标的建议生成的计算瓶颈。

Oriented RCNN

Oriented RCNN是two-stage检测器，包含oriented RPN和oriented RCNN head两部分。其中oriented RPN用于生成高质量的oriented proposal，oriented rcnn head用于分类和回归。FPN采用$\{P_2,P_3,P_4,P_5,P_6\}$，

Oriented RPN

Oriented RPN对输入的任意大小的图像提取oriented proposal。整个结构是一个轻量化的全卷积网络。

具体来说，oriented RPN输入FPN的$\{P_2,P_3,P_4,P_5,P_6\}$五层特征，然后对每一层都有一个$3\times 3$的卷积层和两个sibling（兄弟）的$1\times 1$的卷积层，一个用作分类一个用作回归。在所有的特征层中，每个位置放置三个anchor分别具有三种长宽比$\{1:2,1:1,2:1\}$。每层特征上的anchor的面积分别是$\{32^2,64^2,128^2,256^2,512^2\}$。每一个anchor用中心和长宽表示。回归分支输出6维：$\delta =({\delta }_x,{\delta }_y,{\delta }_w,{\delta }_h,{\delta }_{\alpha },{\delta }_{\beta })$。如前面所述，本文中每个位置处的anchor数量$A=3$。综上，回归分支共有$6A=18$维的输出。根据输出可得oriented proposals:
$$\{\begin{array}{r}\Delta \alpha ={\delta }_a\cdot w,\Delta \beta ={\delta }_{\beta }\cdot h\\ w=a_w\cdot e^{{\delta }_w},h=a_h\cdot e^{{\delta }_h}\\ x={\delta }_x\cdot a_w+a_x,y={\delta }_y\cdot a_h+a_y\end{array}$$
其中$(x,y)$是proposal的中心坐标，$w$和$h$分别是oriented proposal外接矩形的宽和高，$\Delta \alpha$和$\Delta \beta$分别是oriented proposal相对于外接矩形中点的长和高。Oriented RPN很自然的源于RPN，但是其关键在于OBB的表示方法即Midpoint Offset Representation。

Midpoint Offset Representation

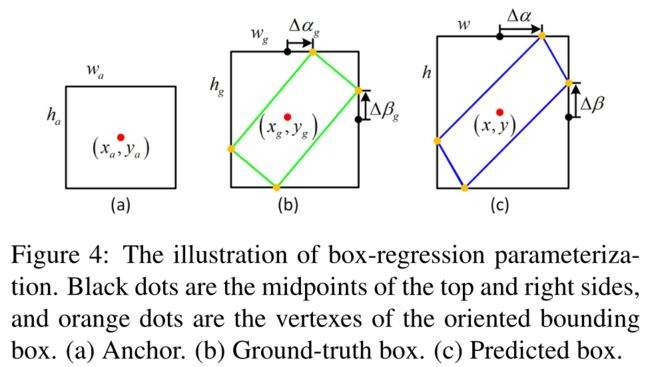
作者提出了一种新的OBB表示方式，称之为中点偏移表示法MOR。如图所示（oriented proposal简称为O），oriented proposal的外接矩形的中点为$(x,y)$，黑点为外接矩形的四条边的中点，橙色点为O的顶点。一个O可以由六个参数表示：$O=(x,y,w,h,\Delta \alpha ,\Delta \beta )$。通过这种表示方法可以得到O的四个顶点的坐标：
$$\{\begin{array}{rlrlr}{v}_1& =& (x,y-\frac{h}{2})+(\Delta \alpha ,0)& =& (x+\Delta \alpha ,y-\frac{h}{2})\\ v_2& =& (x+\frac{w}{2},y)+(0,\Delta \beta )& =& (x+\frac{w}{2},y+\Delta \beta )\\ v_3& =& (x,y+\frac{h}{2})+(-\Delta \alpha ,0)& =& (x-\Delta \alpha ,y+\frac{h}{2})\\ v_4& =& (x-\frac{w}{2},y)+(0,-\Delta \beta )& =& (x-\frac{w}{2},y-\Delta \beta )\end{array}$$
因此，在Oriented RCNN中，oriented RPN输出六个参数来确定oriented proposal。

Loss Function

在训练时，对每一个anchor给定一个binary label，0为负样本，1为正样本。以下2种情况：

1. anchor与任意ground truth的IoU大于0.7；
2. anchor与ground truth的IoU最大且大于0.3，当小于0.3时认为是负样本。

不为正或负样本的anchor训练时被忽略。上述均值的是oriented proposal的外接矩形。

因此损失函数$L_1$定义如下：
$$L_1=\frac{1}{N}\sum _{i=1}^N{F}_{cls}(p_i,p_i^{\ast })+\frac{1}{N}{p}_i^{\ast }\sum _{i=1}^N{F}_{reg}({\delta }_i,t_i^{\ast })$$
其中$i$是anchor的索引，$N$是mini-batch中的样本总数，默认为256。$p_i^{\ast }$是真值标签，$p_i$是分类分支的输出，表示anchor为前景的概率。$t_i^{\ast }$是anchor的真值偏移监督量$t_i^{\ast }=(t_x^{\ast },t_y^{\ast },t_w^{\ast },t_h^{\ast },t_{\alpha }^{\ast },t_{\beta }^{\ast })$，由下式得出：
$$\{\begin{array}{rlr}{\delta }_{\alpha }=\frac{\Delta \alpha }{w},& & {\delta }_{\beta }=\frac{\Delta \beta }{h}\\ {\delta }_w=\log \frac{w}{w_a},& & {\delta }_h=\log \frac{h}{h_a}\\ {\delta }_x=\frac{(x-x_a)}{w_a},& & {\delta }_y=\frac{(y-y_a)}{h_a}\\ t_{\alpha }^{\ast }=\frac{\Delta {\alpha }_g}{w_g},& & t_{\beta }^{\ast }=\frac{\Delta {\beta }_g}{h_g}\\ t_w^{\ast }=\log \frac{w_g}{w_a},& & t_h^{\ast }=\log \frac{h_g}{h_a}\\ t_x^{\ast }=\frac{(x_g-x_a)}{w_a},& & t_y^{\ast }=\frac{(y_g-y_a)}{h_a}\end{array}$$
其中，不带下标的量为网络输出，下标为g为真值，下标为a为anchor。$F_{cls}$是交叉熵损失，$F_{reg}$是Smooth L1损失。

网络输出 ——> 计算输出的oriented proposal ——> 根据anchor计算输出偏移量 ——> 计算损失

真值 ——> 根据anchor计算监督量 ——> 计算损失

Oriented RCNN head

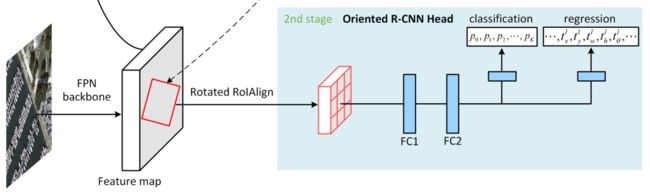
ORH的输入为$\{P_2,P_3,P_4,P_5,P_6\}$。在每个oriented proposal进行oriented RoIAlign从相应层特征中提取固定维度的特征向量，之后经过两个全连接层，在经过两个sibling的全连接层，得到分类输出和回归输出。

Rotated RoIAlign

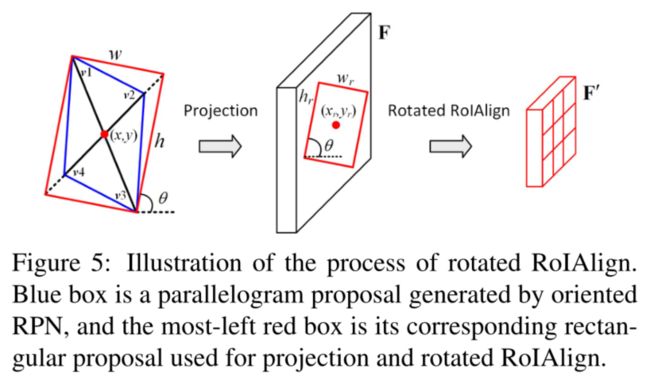
RRoI Align用于提取oriented proposal的旋转不变特征。如图所示，oRPN的输出一般是平行四边形（蓝色框）。为便于计算，需要将平行四边形调整为矩形，该步骤通过延长较短的对角线至与另一对角线相等实现。之后得到图中红色框所示的矩形$(x,y,w,h,\theta )$，其中$\theta \in [-\pi /2,\pi /2]$，是矩形长边与x轴的夹角（锐角）。

接下来将oriented rectangle映射到特征图F上，按照步长s，来获得RRoI：$(x_r,y_r,w_r,h_r,\theta )$：
$$\{\begin{array}{rlr}{w}_r=w/s,& & h_r=h/s\\ x_r=\lfloor x/s\rfloor ,& & y_r=\lfloor y/s\rfloor \end{array}$$
然后每一个RRoI被划分为$m\times m$的网格（文中m=7）来获取固定尺寸的特征$F^{\prime }=m\times m\times C$，在通道c中的个网格$(i,j)$中，其特征值为：
$$F_c^{\prime }(i,j)=\sum _{(x,y)\in area(i,j)}{F}_c(R(x,y,\theta ))/n$$
其中$F_c$是输入特征的第c个通道，$area(i,j)$是网格中的点的坐标集，$R$是旋转变换，与RoI Transformer一致。

Implentation Details

通过oRPN和oRH的联合优化进行端到端的训练。Inference阶段中oRPN的输出往往重叠较高，因此在FPN的每一层中保留最多2000个proposal，然后进行NMS。为了提高Inference的速度，NMS对HBB进行，IoU阈值取0.3。再将剩下的不同层特征中的proposal进行合并，最后根据其score排序选择前1000作为stage2的输入。

在stage2中，对每一个score大于0.05的预测结果进行类内poly NMS，阈值为0.1。

Experiment

Dateset

DOTA和HRSC2016

Parameter settings

用1张2080Ti进行训练，batch size取2。test也在一块2080Ti上。在mmdetection平台上进行实现，backbone为ResNet50和ResNet101，在ImageNet上进行了预训练。训练时采用了水平翻转和竖直反转作为数据增强策略。采用SGD对整个网络进行优化，$momentum=0.9,weigh{t}_{d}ecay=0.0001$。

针对DOTA数据集，文中将原始图像才建成$1024\times 1024$的patch，裁剪步长为824，因此相邻两个patch之间重叠200像素。多尺度训练时，首先将图像调整为原始尺寸的$\{0.5,1.0,1.5\}$，然后再以524为步长，裁剪成$1024\times 1024$的patch。一共训练12 epoch，初始的学习率设为0.005，在第8和第11个epoch中衰减为原来的0.1。合并patch时poly NMS的阈值为0.1。

针对HRSC数据集，不改变图像的长宽比。短边被缩放到800，长边小于等于1333。共训练36个epoch，初始学习率0.005，在第24和第33个epoch中衰减为原来的0.1。

Evaluation of Oriented RPN

从召回率角度评价了oRPN，采用了DOTA的validation set，backbone采用了ResNet-50-FPN。为简化流程，作者只在裁剪的patch上计算召回率，而进行合并。与ground-truth的IoU阈值为0.5。在每个patch中分别选择前300、前1000、前2000个proposal，记为$R_{300}$、$R_{1000}$和$R_{2000}$。如图所示，按$R_{2000}$计算oRPN可以达到92.80%的召回率。$R_{1000}$仅比$R_{2000}$下降了0.6%，但是$R_{300}$的召回率急剧下降。

因此，为了速度和精度，作者在两个数据集上测试时都采用1000个proposal的ORH的输入。本文提出的oRPN可以很好地定位对象，无论其大小、纵横比、方向和密度。

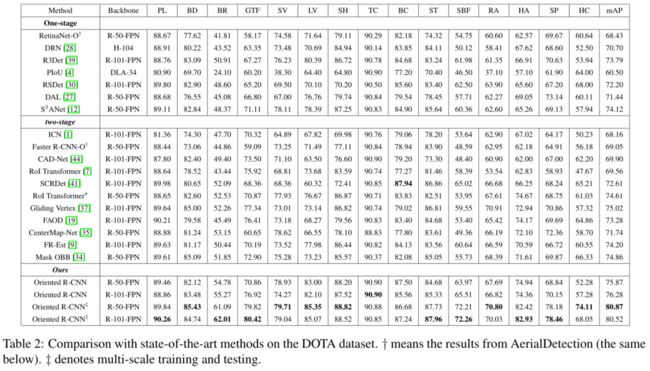
Comparison with State-of-the-Arts

Speed versus Accuracy

在相同的设定条件下，作者比较了不同方法的速度和准确度。对比结果如表4所示。所有方法均采用ResNet-50-FPN作为backbone。测试的硬件平台均为1张2080Ti，batch size为1。在测试时，输入图像的大小为$1024\times 1024$。如表所示，Oriented RCNN比其他方法有更高的检测准确率(75.87% mAP)，但运行速度相当(15.1 FPS)。Oriented RCNN的速度几乎接近于one-stage检测器，但精度远高于one-stage检测器。

Conclusions

本文提出了一种实用的two-stage检测器Oriented RCNN，用于图像中任意方向的目标检测。本文在两个具有挑战性的benchm上进行了广泛的实验。实验结果表明，该方法与目前先进的两级探测器相比具有相当的精度，同时与one-stage检测器相比具有相当的效率。