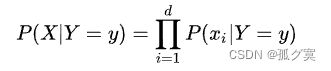机器学习-朴素贝叶斯（垃圾邮件分类）

朴素贝叶斯

朴素贝叶斯定义

        朴素贝叶斯法（Naive Bayes model）是基于贝叶斯定理与特征条件独立假设的分类方法 。朴素贝叶斯方法是在贝叶斯算法的基础上进行了相应的简化，即假定给定目标值时属性之间相互条件独立。也就是说没有哪个属性变量对于决策结果来说占有着较大的比重，也没有哪个属性变量对于决策结果占有着较小的比重。虽然这个简化方式在一定程度上降低了贝叶斯分类算法的分类效果，但是在实际的应用场景中，极大地简化了贝叶斯方法的复杂性。

算法原理

        朴素贝叶斯分类（NBC）是以贝叶斯定理为基础并且假设特征条件之间相互独立的方法，先通过已给定的训练集，以特征词之间独立作为前提假设，学习从输入到输出的联合概率分布，再基于学习到的模型，输入X 求出使得后验概率最大的输出Y。

        

        设有样本数据集D={d ,dg,… , dn}，对应样本数据的特征属性集为X= {a1 , a2, … " , aa}类变量为Y={91, 2,…,ym}，即D可以分为ym类别。其中a1, a2, … , a相互独立且随机，则Y的先验概率
Porion = P(Y)，Y的后验概率Ppost = P(Y|IX)，由朴素贝叶斯算法可得，后验概率可以由先验概率Ppriop =P(Y).证据P(X)、类条件概率P(X|Y)计算出:

                                        

 朴素贝叶斯基于各特征之间相互独立，在给定类别为y 的情况下，上式可以进一步表示为下式：

                        ​​​​​​​        ​​​​​​​        

 由以上两式可以计算出后验概率为：

 由于P(X)的大小是固定不变的，因此在比较后验概率时，只比较上式的分子部分即可。因此可以得到一个样本数据属于类别xi的朴素贝叶斯计算：

优缺点

优点

朴素贝叶斯算法假设了数据集属性之间是相互独立的，因此算法的逻辑性十分简单，并且算法较为稳定，当数据呈现不同的特点时，朴素贝叶斯的分类性能不会有太大的差异。换句话说就是朴素贝叶斯算法的健壮性比较好，对于不同类型的数据集不会呈现出太大的差异性。当数据集属性之间的关系相对比较独立时，朴素贝叶斯分类算法会有较好的效果。 [3] 

缺点

属性独立性的条件同时也是朴素贝叶斯分类器的不足之处。数据集属性的独立性在很多情况下是很难满足的，因为数据集的属性之间往往都存在着相互关联，如果在分类过程中出现这种问题，会导致分类的效果大大降低。

 算法实现

导入库

import numpy as np
import random
import re

数据导入

数据集（链接: https://pan.baidu.com/s/1OjIJTnmTmuFrQ6u1_87gcw 提取码: 1snc ）

def spamTest():
    docList = []
    classList = []
    fullText = []
    for i in range(1, 26):
        wordList = textParse(open('D:/learn/three first/machine learning/data/spam/%d.txt' % i).read())  # spam文件夹中的邮件全设为1
        docList.append(wordList)
        fullText.extend(wordList)
        classList.append(1)
        wordList = textParse(open('D:/learn/three first/machine learning/data/ham/%d.txt' % i).read())  # ham文件夹中的邮件全设为0
        docList.append(wordList)
        fullText.extend(wordList)
        classList.append(0)
    vocabList = createVocabList(docList)  # 将重复出现的单词删掉
    trainingSet = list(range(50))
    testSet = []
    # 随机选取20封邮件为测试集
    for i in range(20):
        randIndex = int(random.uniform(0, len(trainingSet)))
        testSet.append(trainingSet[randIndex])
        del (trainingSet[randIndex])  # 将测试集从训练集中删除
    trainMat = []
    trainClasses = []
    # 剩下的30封作为训练集
    for docIndex in trainingSet:
        trainMat.append(setOfWords2Vec(vocabList, docList[docIndex]))  # 将文本转换成向量
        trainClasses.append(classList[docIndex])
    p0V, p1V, pSpam = trainNB0(np.array(trainMat), np.array(trainClasses))  # 贝叶斯算法来计算概率
    rightCount = 0
    # 测试集分类精度计算
    for docIndex in testSet:
        wordVector = setOfWords2Vec(vocabList, docList[docIndex])
        print("the index %d is classified as: %d, the real class is %d" % (
        docIndex, classifyNB(np.array(wordVector), p0V, p1V, pSpam), classList[docIndex]))
        if classifyNB(np.array(wordVector), p0V, p1V, pSpam) == classList[docIndex]:
            rightCount += 1
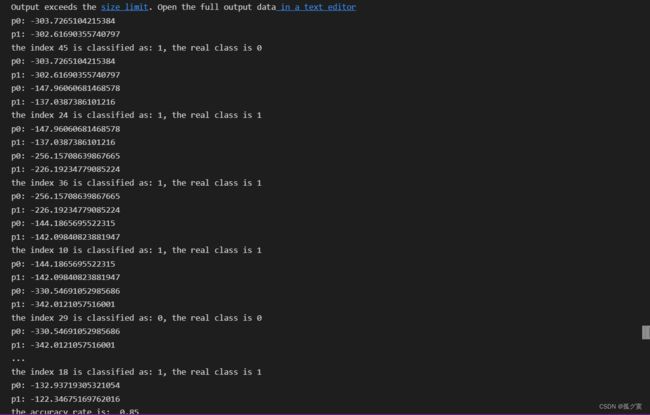
    print('the accuracy rate is: ', float(rightCount) / len(testSet))

朴素贝叶斯交叉验证 

def textParse(bigString):
    listOfTokens = re.split(r'\W+', bigString)
    return [tok.lower() for tok in listOfTokens if len(tok) > 2]

创建词汇表

def createVocabList(dataSet):
    vocabSet = set([])  # 创建空集合
    for document in dataSet:
        vocabSet = vocabSet | set(document)  # 返回不重复的单词集合
        # print(vocabSet)
    return list(vocabSet)

 构建词袋

def setOfWords2Vec(vocabList, inputSet):
    returnVec = [0] * len(vocabList)
    for word in inputSet:
        if word in vocabList:
            returnVec[vocabList.index(word)] = 1
        else:
            print("the word: %s is not in my Vocabulary!" % word)
    return returnVec

 构造分类器训练函数 

# trainMatrix为输入的词条集合,trainCategory为词条类别
def trainNB0(trainMatrix, trainCategory):
    numTrainDocs = len(trainMatrix)  # 获取词条长度,即分母变量
    numWords = len(trainMatrix[0])  # 第一段词条中单词个数,即分子变量
    pAbusive = sum(trainCategory) / float(numTrainDocs)
    p0Num = np.ones(numWords)
    p1Num = np.ones(numWords)
    p0Denom = 2.0
    p1Denom = 2.0
    for i in range(numTrainDocs):
        if trainCategory[i] == 1:
            p1Num += trainMatrix[i]
            p1Denom += sum(trainMatrix[i])
        else:
            p0Num += trainMatrix[i]
            p0Denom += sum(trainMatrix[i])
    p1Vect = np.log(p1Num / p1Denom)
    p0Vect = np.log(p0Num / p0Denom)
    return p0Vect, p1Vect, pAbusive

 实现分类器 

# 分类,取概率高的值
# 1是垃圾邮件 0是非垃圾邮件
def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
    p1 = sum(vec2Classify * p1Vec) + np.log(pClass1)
    p0 = sum(vec2Classify * p0Vec) + np.log(1.0 - pClass1)
    print('p0:', p0)
    print('p1:', p1)
    if p1 > p0:
        return 1
    else:
        return 0

测试 

if __name__ == '__main__':
    spamTest()

 结果分析

        结果准确率为0.85 ，可以看出错误率并不高，朴素贝叶斯分类算法对文本分类是学习效率和分类效果较好的分类器之一。

参考文献

《机器学习实战》