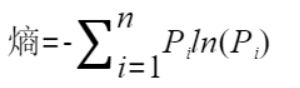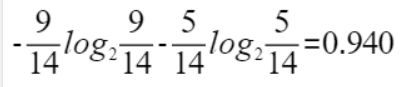决策树原理及代码实现

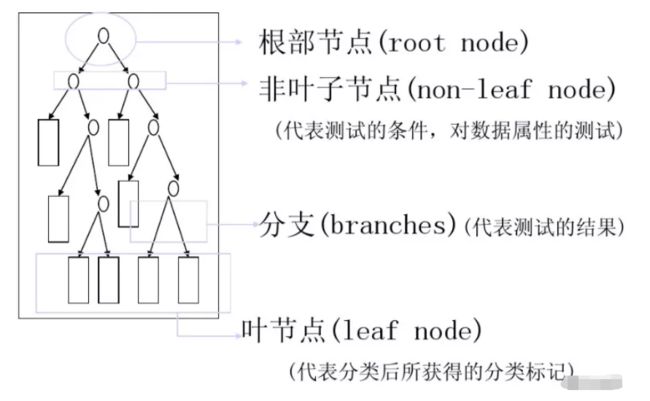
决策树(Decision Tree,又称为判定树)算法是机器学习中常见的一类算法，是一种以树结构(包括二叉树和多叉树)形式表达的预测分析模型。每个决策点实现一个具有离散输出的测试函数，记为分支。决策树由结点和有向边组成。结点有两种类型: 内部结点和叶节点。内部节点表示一个特征或属性，叶节点表示一个类。

一、决策树的结构

决策树通常有三个步骤：特征选择、决策树生成、决策树的修建。
特征选择是建立决策树之前十分重要的一步。如果是随机地选择特征，那么所建立决策树的学习效率将会大打折扣。通常我们在选择特征时，会考虑到两种不同的指标，分别为：信息增益和信息增益比。要想弄清楚这两个概念，我们就不得不提到信息论中的另一个十分常见的名词 —— 熵。熵（Entropy）是表示随机变量不确定性的度量。简单来讲，熵越大，随机变量的不确定性就越大。而特征 A 对于某一训练集 D 的信息增益 g(D, A) 定义为集合 D 的熵 H(D) 与特征 A 在给定条件下 D 的熵 H(D/A) 之差。

二、决策树分两个阶段

1、训练阶段
从给定的训练数据集DB，构造出一颗决策树
class=DecisionTree(DB)
2、分类阶段
从根开始，按照决策树的分类属性逐层往下划分，直到叶节点，获得概念（决策、分类）结果。
y=DecisionTree(x)

三、决策树熵原理

熵：代表的是一个混乱程度
假设X和Y两个事件相互独立，则P(X,Y)=P(X)*P(Y)，Log(XY)=Log(X)+Log(Y)
H(X),H(Y)：事件发生的不确定性
P(几率越大)->H(X)值越小->熵值越小

P(几率越小)->H(X)值越大->熵值越大

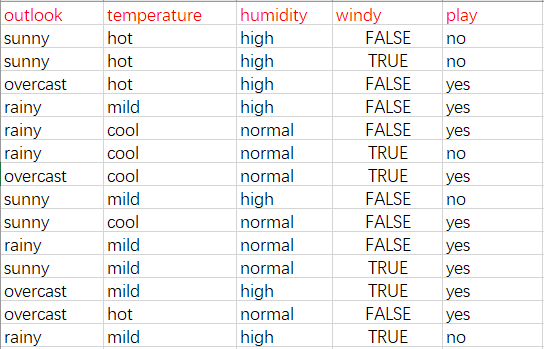
0

尼基系数和熵值的定义类似，尼基系数越大，熵值也越大，说明越混乱。

四、构造决策树根节点

决策树的基本思想是随着树深度的增加，节点的熵迅速地降低。熵降低的速度越快越好，这样我们构造的决策树是一颗高度最矮的决策树（分支过多容易出现过拟合的现象），我们举一个实例来看一下：

这是根据天气状况决定是否出去打球的数据

14行数据，每行数据4个特征

在没有给定任何天气信息时，根据历史数据，我们只知道新的一天打球的概率是9/14，不打的概率是5/14，此时的熵为：

接下来我们分别求出四个特征条件下的信息熵：
以outlook为例：
当outlook=sunny时，2/5的概率打球，3/5的概率不打球，entropy=0.971
当outlook=overcast时，entropy=0
当outlook=rainy时，entropy=0.971
而根据历史统计数据，outlook取值为sunny、overcast、rainy的概率分别是5/14、4/14、5/14，所以当已知变量outlook的值时，信息熵为：
5/14 x 0.971 + 4/14 x 0 + 5/14 x 0.971 = 0.693
这样的话系统熵就从0.940下降到了0.693，信息增益gain(outlook)为0.940-0.693=0.247
同样可以计算出gain(temperture)=0.029，gain(humidity)=0.152，gain(windy)=0.048。gain(outlook)最大（即outlook在第一步使系统的信息熵下降的最快），所以决策树的根节点就去outlook。其余子节点的求法和根节点类似，所以决策树算法是一个递归算法。
我们使用代码实现一下：

from math import log
def createDataSet():
    #outlook:sunny:1,overcast:2,rainy:3
    #temperature:hot:1,mild:2,cool:3
    #humidity:high:1,normal:2
    #windy:false:1,true:2
    #play:no,yes
    dataSet=[
        [1,1,1,1,'no'],
        [1,1,1,2,'no'],
        [2,1,1,1,'yes'],
        [3,2,1,1,'yes'],
        [3,3,2,1,'yes'],
        [3,3,2,2,'no'],
        [2,3,2,2,'yes'],
        [1,2,1,1,'no'],
        [1,3,2,1,'yes'],
        [3,2,2,1,'yes'],
        [1,2,2,2,'yes'],
        [2,2,1,2,'yes'],
        [2,1,2,1,'yes'],
        [3,2,1,2,'no']
    ]
    labels=['outlook','temperature','humidity','windy','play']
    return dataSet,labels
def calcShannonEnt(dataSet):
    #返回数据集行数
    numEntries=len(dataSet)
    #保存每个标签（label）出现次数的字典
    labelCounts={}
    #对每组特征向量进行统计
    for featVec in dataSet:
        currentLabel=featVec[-1]#提取标签信息
        if currentLabel not in labelCounts.keys():#如果标签没有放入统计次数
            labelCounts[currentLabel]=0
        labelCounts[currentLabel]+=1#label计数
    shannonEnt=0.0
    #计算经验熵
    for key in labelCounts:
        prob=float(labelCounts[key])/numEntries #选择该标签的概率
        shannonEnt-=prob*log(prob,2)            #利用公式计算
    return shannonEnt
def chooseBestFeatureToSplit(dataSet):
    #特征数量
    numFeatures = len(dataSet[0]) - 1
    #计数数据集的香农熵
    baseEntropy = calcShannonEnt(dataSet)
    #信息增益
    bestInfoGain = 0.0
    #最优特征的索引值
    bestFeature = -1
    #遍历所有特征
    for i in range(numFeatures):
        # 获取dataSet的第i个所有特征
        featList = [example[i] for example in dataSet]
        #创建set集合{}，元素不可重复
        uniqueVals = set(featList)
        #经验条件熵
        newEntropy = 0.0
        #计算信息增益
        for value in uniqueVals:
            #subDataSet划分后的子集
            subDataSet = splitDataSet(dataSet, i, value)
            #计算子集的概率
            prob = len(subDataSet) / float(len(dataSet))
            #根据公式计算经验条件熵
            newEntropy += prob * calcShannonEnt((subDataSet))
        #信息增益
        infoGain = baseEntropy - newEntropy
        #打印每个特征的信息增益
        print("第%d个特征的增益为%.3f" % (i, infoGain))
        #计算信息增益
        if (infoGain > bestInfoGain):
            #更新信息增益，找到最大的信息增益
            bestInfoGain = infoGain
            #记录信息增益最大的特征的索引值
            bestFeature = i
            #返回信息增益最大特征的索引值
    return bestFeature
def splitDataSet(dataSet,axis,value):
    retDataSet=[]
    for featVec in dataSet:
        if featVec[axis]==value:
            reducedFeatVec=featVec[:axis]
            reducedFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reducedFeatVec)
    return retDataSet
if __name__=='__main__':
    dataSet,features=createDataSet()
    print(dataSet)
    print(calcShannonEnt(dataSet))
    print("最优索引值："+str(chooseBestFeatureToSplit(dataSet)))

实验结果

五、决策树算法

ID3:信息增益
C4.5:信息增益率
CART：Gini系数

评价函数：

其中t是叶子节点
ID3 算法通过递归的方式建立决策树。建立时，从根节点开始，对节点计算每个独立特征的信息增益，选择信息增益最大的特征作为节点特征。接下来，对该特征施加判断条件，建立子节点。然后针对子节点再此使用信息增益进行判断，直到所有特征的信息增益很小或者没有特征时结束，这样就逐步建立一颗完整的决策树。除了从信息增益演化而来的 ID3 算法，还有一种常见的算法叫 C4.5。C4.5 算法同样由 John Ross Quinlan 发明，但它使用了信息增益比来选择特征，这被看成是 ID3 算法的一种改进。C4.5算法能够处理连续型的属性。首先将连续型属性离散化，把连续型属性的值分成不同的区间，依据是比较各个分裂点Gian值得大小，关于缺失数据在构建决策树时，可以简单地忽略缺失数据，即在计算增益时，仅考虑具有属性值的记录。
ID3 和 C4.5 算法简单高效，但是他俩均存在一个缺点，那就是用“完美去造就了另一个不完美”。这两个算法从信息增益和信息增益比开始，对整个训练集进行的分类，拟合出来的模型针对该训练集的确是非常完美的。但是，这种完美就使得整体模型的复杂度较高，而对其他数据集的预测能力就降低了，也就是我们常说的过拟合而使得模型的泛化能力变弱。

CART 算法本身就包含了决策树的生成和修剪，并且可以同时被运用到分类树和回归树。这就是和 ID3 及 C4.5 之间的最大区别。
当然，过拟合的问题也是可以解决的，那就是对决策树进行修剪。

六、决策树的剪枝策略

决策树的修剪，其实就是通过优化损失函数来去掉不必要的一些分类特征，降低模型的整体复杂度。修剪的方式，就是从树的叶节点出发，向上回缩，逐步判断。如果去掉某一特征后，整棵决策树所对应的损失函数更小，那就将该特征及带有的分支剪掉。
剪枝策略分为两种：
预剪枝：在构建决策树的过程时，提前停止
后剪枝：决策树构建好后，然后才开始裁剪

七、鸢尾花分类实验

数据集的介绍

鸢尾花数据集是机器学习领域一个非常经典的分类数据集。数据集名称的准确名称为 Iris DataSet,总共包含 150 行数据。每一行数据由 4 个特征值及一个目标值组成。其中 4 个特征值分别为：萼片长度、萼片宽度、花瓣长度、花瓣宽度。该数据集可以直接从网上下载，网上有很多关于该数据集的介绍，如果找不到可以在下方留言或者私信我。

#导入数据集
import pandas as pd
iris_data = pd.read_csv('F:\\BaiduNetdiskDownload\\决策树\\决策树鸢尾花\\iris.data')
#指定列名
iris_data.columns = ['sepal_length_cm', 'sepal_width_cm', 'petal_length_cm', 'petal_width_cm', 'class']
iris_data.head()

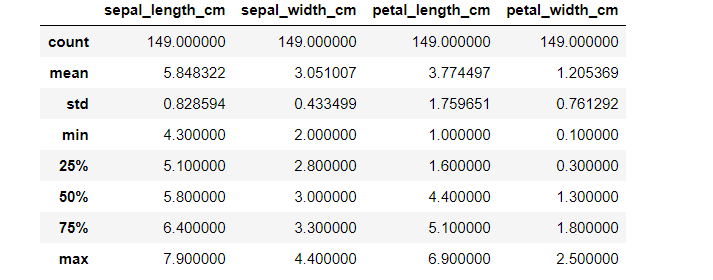
#查看一下数据集的信息
iris_data.describe()#特征之间数据的分布

这里我们使用seaborn来进行绘图操作，它比matplotlib更方便直观一点：

%matplotlib inline
import matplotlib.pyplot as plt
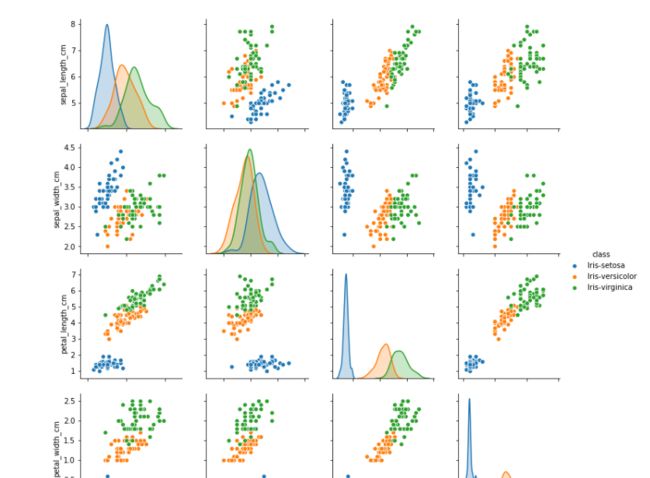
import seaborn as sb
sb.pairplot(iris_data.dropna(), hue='class')#不能有缺失值

plt.figure(figsize=(10, 10))
for column_index, column in enumerate(iris_data.columns):
    if column == 'class':
        continue
    plt.subplot(2, 2, column_index + 1)
    sb.violinplot(x='class', y=column, data=iris_data)#小提琴图

接下来我们进行数据集的划分：

from sklearn.cross_validation import train_test_split
all_inputs = iris_data[['sepal_length_cm', 'sepal_width_cm',
                             'petal_length_cm', 'petal_width_cm']].values

all_classes = iris_data['class'].values

(training_inputs,
 testing_inputs,
 training_classes,
 testing_classes) = train_test_split(all_inputs, all_classes, train_size=0.75, random_state=1)

然后我们使用Scikit-learn包引入决策树算法，Scikit-learn(sklearn)是机器学习中常用的第三方模块，对常用的机器学习方法进行了封装。但是DecisionTreeClassifier() 模型方法中也包含非常多的参数值，这里列举一下：

#使用决策树算法进行分析
from sklearn.tree import DecisionTreeClassifier
#  1.criterion  gini  or  entropy 基尼系数和熵值的选择

#  2.splitter  best or random 前者是在所有特征中找最好的切分点 后者是在部分特征中（数据量大的时候）

#  3.max_features  None（所有），log2，sqrt，N  特征小于50的时候一般使用所有的
#剪枝操作
#  4.max_depth  数据少或者特征少的时候可以不管这个值，如果模型样本量多，特征也多的情况下，可以尝试限制下
#要不要停止操作
#  5.min_samples_split  如果某节点的样本数少于min_samples_split，则不会继续再尝试选择最优特征来进行划分
#                       如果样本量不大，不需要管这个值。如果样本量数量级非常大，则推荐增大这个值。

#  6.min_samples_leaf  这个值限制了叶子节点最少的样本数，如果某叶子节点数目小于样本数，则会和兄弟节点一起被
#                      剪枝，如果样本量不大，不需要管这个值，大些如10W可是尝试下5

#  7.min_weight_fraction_leaf 这个值限制了叶子节点所有样本权重和的最小值，如果小于这个值，则会和兄弟节点一起
#                          被剪枝默认是0，就是不考虑权重问题。一般来说，如果我们有较多样本有缺失值，
#                          或者分类树样本的分布类别偏差很大，就会引入样本权重，这时我们就要注意这个值了。

#  8.max_leaf_nodes 通过限制最大叶子节点数，可以防止过拟合，默认是"None”，即不限制最大的叶子节点数。
#                   如果加了限制，算法会建立在最大叶子节点数内最优的决策树。
#                   如果特征不多，可以不考虑这个值，但是如果特征分成多的话，可以加以限制
#                   具体的值可以通过交叉验证得到。

#  9.class_weight 指定样本各类别的的权重，主要是为了防止训练集某些类别的样本过多
#                 导致训练的决策树过于偏向这些类别。这里可以自己指定各个样本的权重
#                 如果使用“balanced”，则算法会自己计算权重，样本量少的类别所对应的样本权重会高。

#  10.min_impurity_split 这个值限制了决策树的增长，如果某节点的不纯度
#                       (基尼系数，信息增益，均方差，绝对差)小于这个阈值
#                       则该节点不再生成子节点。即为叶子节点 。
#定义一个决策树的对象
decision_tree_classifier = DecisionTreeClassifier()
#训练模型
# Train the classifier on the training set
decision_tree_classifier.fit(training_inputs, training_classes)
#所得模型的准确性
# Validate the classifier on the testing set using classification accuracy
decision_tree_classifier.score(testing_inputs, testing_classes)

准确性

from sklearn.cross_validation import cross_val_score#交叉验证交叉验证用于评估模型的预测性能，尤其是训练好的模型在新数据上的表现，可以在一定程度上减小过拟合。还可以从有限的数据中获取尽可能多的有效信息。
import numpy as np
decision_tree_classifier = DecisionTreeClassifier()

# cross_val_score returns a list of the scores, which we can visualize
# to get a reasonable estimate of our classifier's performance
cv_scores = cross_val_score(decision_tree_classifier, all_inputs, all_classes, cv=10)#cv：选择每次测试折数 
print (cv_scores)
#kde=False
sb.distplot(cv_scores)
plt.title('Average score: {}'.format(np.mean(cv_scores)))

我们设置一下参数，查看运行结果：

decision_tree_classifier = DecisionTreeClassifier(max_depth=1)

cv_scores = cross_val_score(decision_tree_classifier, all_inputs, all_classes, cv=10)
print (cv_scores)
sb.distplot(cv_scores, kde=False)
plt.title('Average score: {}'.format(np.mean(cv_scores)))

我们使用GridSearchCV网格搜索进行自动调参，把参数输进去，能给出最优化的结果和参数：

from sklearn.grid_search import GridSearchCV
from sklearn.cross_validation import StratifiedKFold

decision_tree_classifier = DecisionTreeClassifier()

parameter_grid = {'max_depth': [1, 2, 3, 4, 5],
                  'max_features': [1, 2, 3, 4]}

cross_validation = StratifiedKFold(all_classes, n_folds=10)

grid_search = GridSearchCV(decision_tree_classifier,
                           param_grid=parameter_grid,
                           cv=cross_validation)

grid_search.fit(all_inputs, all_classes)
print('Best score: {}'.format(grid_search.best_score_))
print('Best parameters: {}'.format(grid_search.best_params_))

运行结果

八、决策树的优缺点以及改进

• 优点：
  1、简单易理解和解释，树木可视化
  2、需要很少的数据准备，其他技术通常需要数据归一化
• 缺点：
  决策树学习者可以创建不能很好的推广数据的过于复杂的树，这被称为过拟合
• 改进：
  1、剪枝cart算法（决策树API当中已经实现，随机森林参数调优有相关介绍）
  2、随机森林

九、集成学习方法——随机森林

1、集成学习

集成学习童工建立几个模型组合来解决单一预测问题。它的工作原理是生成多个分类器/模型，各自独立的学习和做出预测，这些预测最后结合成单预测，因此优于任何一个单分类做出来的预测。

2、随机森林

在机器学习中，随机森林是一个包含多个决策树的分类器，并且其输出的类别是由个别树输出的类别的众数而定。

• 随机森林建立多个决策树的过程(N个样本，M个特征)
  1、随机在N个样本当中选择一个样本，重复N次，样本有可能重复
  2、随机在M个特征当中选出m个特征（m< 3、采用bootstrap抽样（随机有放回的抽样）
  为什么要随机抽样训练集：
  如果不随机抽样，每棵树的训练集都一样，那么最终训练出的树分类结果也是完全一样的
  为什么要有放回的抽样：
  如果不是有放回的抽样，那么每棵树的训练样本都是不同的，都是没有交集的，这样每棵树都是"有偏的"，都是绝对"片面的"（当然这样说可能不对），也就是说每棵树训练出来都是有很大差异的，而随机森林最后分类取决于多棵树（弱分类器）的投票表决。

3、随机森林分类器的API

由于随机森林API的参数众多，这里我们就选择部分常用的进行介绍：
sklearn.ensemble.RandomForestClassifier(n_estimators=10,criterion='gini',max_depth=None,bootstrap=True,random_state=None)

参数	说明
n_estimators	integer,optional(default=10)森林里的树木数量120，200，300，500，800，1200
criteria	string,可选（default="gini"）分割特征的测量方法
max_depth	integer或None,可选（默认=无）树的最大深度5，8，15，25，30
max_features	每个决策树的最大特征数量,若max_features="auto"或者"sqrt"，则'max_features=sqrt(n_features),若max_features="log2"则'max_features=log2(n_features)'，若max_features="None"则'max_features=n_features'
bootstrap	boolean,optional(default = True)是否在构建树时使用放回抽样

4、案例分析

这里补充一点，决策树可视化问题，通过sklearn.tree.export_graphviz()可以将树导出成DOT格式，然后使用graphviz工具可以将dot格式转换成png或者jpg格式进行查看dot -Tpng tree.dot -o tree.png

import pandas as pd
from sklearn.feature_extraction import DictVectorizer
from sklearn.model_selection import train_test_split,GridSearchCV
from sklearn.tree import DecisionTreeClassifier,export_graphviz
def Decision():
    """
    决策树预测泰坦尼克生死
    :return:
    """
    #读取数据
    data = pd.read_csv('../../数据集/机器学习/分类算法/Titanic/titanic.csv')
    # print(data.columns.values)
    #处理数据，找出特征值和目标值
    x = data.loc[:,['sex','age','pclass']]
    y = data.loc[:,['survived']]

    #有缺失值，处理缺失值，平均值填充
    x['age'].fillna(x['age'].mean(),inplace = True)

    #划分训练集和测试集
    x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.25)

    #进行字典特征的抽取,特征->类别->one_hot编码（特征里面是类别，值的类型都不同，要进行one_hot编码）
    dict = DictVectorizer(sparse=False)

    x_train = dict.fit_transform(x_train.to_dict(orient="records"))

    x_test = dict.transform(x_test.to_dict(orient="records"))

    # 利用决策树进行分类
    dec = DecisionTreeClassifier(max_depth=5)

    dec.fit(x_train,y_train)

    #预测准确率
    print("准确率为：",dec.score(x_test,y_test))
    print(dict.get_feature_names())

    #导出树的结构
    export_graphviz(dec,out_file='../../数据集/机器学习/分类算法/Titanic/tree.dot',feature_names=['年龄','pclass','女性','男性'])
    return None


if __name__ == "__main__":
    Decision()

我们运行一下之后，会在对应的目录下生成tree.dot

接下来我们安装graphviz，我这里是在windows系统运行的，先讲一下windows的安装方法，首先在官网上下载
graphvizhttps://graphviz.gitlab.io/_pages/Download/Download_windows.html这种格式都可以，安装完后添加到系统变量，windows添加系统变脸我就不说了，直接把目录加载到bin目录下，能看到dot.exe那个文件路径。

添加到系统变量中后，打开dos命令行，输入

看到输出版本号说明安装成功！

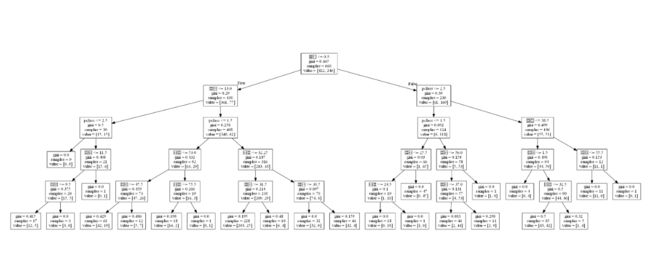
最后我们进入tree.dot的文件中，打开dos命令行输入，

这时文件下就会多出一个tree.png的图片，我们打开就可以看到了。

这就是我们生成的决策树。
接下来我们进行决策树的演练，

import pandas as pd
from sklearn.feature_extraction import DictVectorizer
from sklearn.model_selection import train_test_split,GridSearchCV
from sklearn.tree import DecisionTreeClassifier,export_graphviz
from sklearn.ensemble import RandomForestClassifier
def Decision():
    """
    决策树预测泰坦尼克生死
    :return:
    """
    #读取数据
    data = pd.read_csv('../../数据集/机器学习/分类算法/Titanic/titanic.csv')
    # print(data.columns.values)
    #处理数据，找出特征值和目标值
    x = data.loc[:,['sex','age','pclass']]
    y = data.loc[:,['survived']]

    #有缺失值，处理缺失值，平均值填充
    x['age'].fillna(x['age'].mean(),inplace = True)

    #划分训练集和测试集
    x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.25)

    #进行字典特征的抽取,特征->类别->one_hot编码（特征里面是类别，值的类型都不同，要进行one_hot编码）
    dict = DictVectorizer(sparse=False)

    x_train = dict.fit_transform(x_train.to_dict(orient="records"))

    x_test = dict.transform(x_test.to_dict(orient="records"))

    # 利用决策树进行分类
    # dec = DecisionTreeClassifier(max_depth=5)
    # 
    # dec.fit(x_train,y_train)
    # 
    # #预测准确率
    # print("准确率为：",dec.score(x_test,y_test))
    # print(dict.get_feature_names())
    # 
    # #导出树的结构
    # export_graphviz(dec,out_file='../../数据集/机器学习/分类算法/Titanic/tree.dot',feature_names=['年龄','pclass','女性','男性'])

    #随机森林预测分类（超参数调优）
    rf = RandomForestClassifier()

    param = {"n_estimators":[120,200,300,500,800],"max_depth":[5,8,15,25,30]}

    #网格搜索与交叉验证
    gc = GridSearchCV(rf,param_grid=param,cv=5)

    gc.fit(x_train,y_train)

    #输出准确率
    print("准确率为：",gc.score(x_test,y_test))

    print("选择最好的模型是：",gc.best_estimator_)

    print("每次交叉验证的结果",gc.cv_results_)

    return None


if __name__ == "__main__":
    Decision()

最后得出当 n_estimators=500,max_depth=25模型最好。

十、随机森林算法的优点

这里提一下，随机森林算法几乎没有缺点，唯一的缺点是参数的选取

• 在当前所有算法中，具有极好的准确率
• 能够有效地运行在大数据集上
• 能够处理具有高维特征的输入样本，而且不需要降维
• 能够评估各个特征在分类问题上的重要性

随机森林的用法到这里就结束，有不明白的地方可以私信我。欢迎一起学习，一起进步。

参考链接

1.《统计学习方法》，李航，清华大学出版社
2.https://blog.csdn.net/oxuzhenyi/article/details/76427704
3.鸢尾花(iris)数据集分析 - 简书
4.https://blog.csdn.net/qq_36523839/article/details/80707678
5.b站视频讲解（up主：蓝亚之舟）

文章来源：机器学习(二):决策树原理及代码实现 - 简书