脑电信号功率谱估计

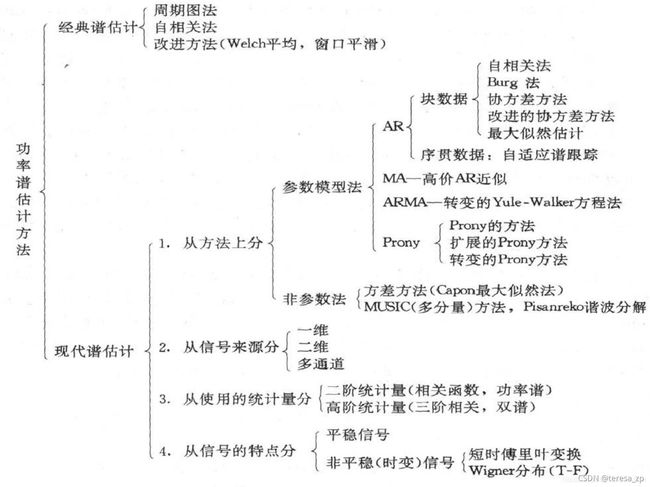
1功率谱估计

功率谱估计是频域分析的主要手段。它的意义在于把幅度随时间变化的脑电波变换为脑电功率随频率变化的谱图，从而可直观地观察到脑电节律的分布与变换情况。

经典功率谱估计采用的是传统傅里叶变换分析方法(又称线性谱估计)，主要包括直接法(又称周期图法)和间接法(又称自相关法)两种。

 

周期图法直接对观测数据进行快速傅里叶变换，得到功率谱。

自相关法先估计自相关函数，再计算功率谱。

由于周期图法直接使用FFT快速计算，所以应用比较广泛。

经典谱估计优点是计算效率高，缺点是频率分辨率低，常用于频率分辨率要求不高的场合。当样本数据很大时经典谱估计的效果是可以接受的，但是样本少时，此估计方法的效果往往不是很好，这是由于经典谱估计的天然缺陷造成的：经典谱估计认为除了样本数据以外的其他信号值全为零，这是不符合实际的，经典谱估计的分辨率低，不可避免的受到加窗的影响，而且它也不是真实的一致估计。

2直接法原理 

直接法又称周期图法，这种功率谱也具有周期性，常称为周期图。

周期图是信号功率谱的一个有偏估值，而且当信号序列的长度增大到无穷时，估值的方差不趋于零。

把随机序列的个观测数据看做能量有限的序列，直接计算的离散傅里叶变换，得，然后再取其幅值的平方，除以，作为序列真实功率谱的估计。

其定义如下： 长度为的实平稳随机信号序列的周期图为:

上式子中,,由于的DFT有周期性，所以也有周期性，是有偏估计。

第一步：计算个数据的傅里叶变换(即频谱)

第二步：取频谱和其共轭的乘积，得到功率谱

[说明：随着所取的信号序列长度的不同，所得到的周期图也不同，这种现象称为随机起伏。由于随机起伏大，使用周期图不能得到比较稳定的估值]

由周期图法得到的功率谱，其估计方差并不随样本长度的增加而趋于零，出人意料的是，不管数据记录有多长，周期图和自相关法得到的估计都不是功率谱的良好估计。事实上，随着记录长度增加，这两种估计的随机起伏反而会更加严重！此外，它们存在着以下两个难以克服的固有缺点。

（1）频率分辨率（区分两个邻近频率分量的能力）不高。因为它们的频率分辨率（赫兹）反比于数据记录长度（秒）（即Δf=k/Tp=k/NT，k为常数，Tp=NT为数据的记录长度，T为采样周期），而实际应用中一般不可能获得很长的数据记录，即观察到的数据只能是有限个，而观察不到的数据被认为是0。这样，如果只有N个观测数据，而对于N以外的数据，信号仍有较强的相关性，那么估计出的功率谱就会出现很大的偏差。

（2）对于有限的观测数据，相当于将信号在时域内乘以矩形窗函数，因而在频域内则相当于使真正的功率谱与sinc函数进行卷积，由于sinc函数不同于δ 函数，它有主瓣和旁瓣，这样使卷积后的功率谱不同于真正的功率谱。sinc函数的主瓣不是无限窄的，引起功率谱向附近频域扩展，造成谱的模糊，降低谱的分辨率；同时，由于sinc函数的旁瓣存在，导致能量向旁瓣中“泄漏”（称之为旁瓣泄漏），即引起频谱间的干扰，信号强的功率谱旁瓣影响信号弱的功率谱检测，严重时，会使主瓣产生很大失真，检测不出弱信号，或者把旁瓣误认为是信号，造成假信号。为了对经典功率谱估计进行改进，可以采用各种不同的窗函数，但其结果都是以增加主瓣宽度来换取旁瓣的压低，因此功率谱分辨率低是经典功率谱估计的致命缺点。

为了克服以上缺点，人们曾做过长期努力，提出了平均、加窗平滑等办法，在一定程度上改善了经典功率谱估计的性能。实践证明，对于长数据记录来说，以傅氏变换为基础的经典功率谱估计方法，的确是比较实用的。但是，经典方法始终无法根本解决频率分辨率和功率谱估计稳定性之间的矛盾，特别是在数据记录很短的情况下，这一矛盾显得尤为突出。这就促进了现代功率谱估计方法研究的展开。

2.1案例说明 

clear;%采样频率

Fs=1000;

n=0:1/Fs:1;%生成含有噪声的信号序列

xn=cos(2*pi*40*n)+3*cos(2*pi*100*n)+randn(size(n));

%设置矩形窗

window=boxcar(length(xn));

nfft=1024;%直接法[Pxx,f]=periodogram(xn,window,nfft,Fs);plot(f,10*log10(Pxx));xlabel('频率/Hz');ylabel('功率/dB')

3现代谱估计

现代谱估计以模型为基础，利用采样数据建立模型，对数据进行外推，进而提高了谱估计的分辨率。但是现代谱估计外推的数据不能完全重构数据，只能用来估计功率谱。

现代功率谱估计方法主要是以随机过程（Stochastic Process）的参数模型（Parameter Model）为基础的，称之为参数模型方法。虽然说现代功率谱估计技术的研究和应用主要起始于60年代，但实际上，时间序列模型在非工程领域早已被采用，如Yule在1927年、Walker在1931年都曾使用过自回归模型预测描述经济的时间序列的发展趋势，而Prony则早在1795年就曾采用指数模型去拟合在气体化学实验中获得的数据。在统计学和数值分析领域中，人们也曾采用过模型方法。

现代功率谱估计的提出主要是针对经典功率谱估计（周期图和自相关法）的分辨率和方差性能不好的问题而提出的。1967年Burg在地震学研究中受到线性预测滤波的启发，提出了最大熵谱估计方法，在提高分辨率方面作了最有意义的探索。1968年Parzen正式提出了自回归谱估计方法。1971年Van der Bos证明了一维最大熵谱估计与自回归谱估计等效。1972年出现的谱估计的Prony方法在数学上与自回归方法有某些类似。目前以自回归滑动平均模型为基础的谱估计已经比自回归模型谱估计具有更高的频率分辨率和更好的性能。1973年Pisarenko提出的谐波分解方法提供了可靠的频率估计方法。1981年Schmidt提出了谱估计的多信号分类（MUSIC）算法等。因此，现代功率谱分析主要有ARMA谱分析、最大似然、熵谱估计和特征分解四种方法。ARMA谱分析是一种建模方法，即通过平稳线性信号过程建立模型来估计功率谱密度；熵谱估计包括最大熵谱和最小交叉法；特征分解也叫特征构造法和子空间法，包括Pisarenko谐波分解法、Prony法、MUSIC法和ESPRIT法（用旋转不变技术估计参数方法）。

4时域分析与频域分析

EEG信号特征提取就是以脑电信号作为源信号，确定各种参数并以此为向量组成表征信号特征的特征向量。

特征參数主要包括时域信号(如幅值)和频域信号(如频率)两大类，相应的特征提取方法也分为时域法、频域法 和时-频域方法。

频域分析方法主要是基于EEG信号各频段功率、相干等。

这类方法是建立在假设EEG信号具有平稳特性的基础上，同时只是考虑信号的频域信息，忽略信号在时间上的分辨率。在EEG信号研究中，常用的频域分析方法包括功率谱估计(直接发和间接法)。

时域分析方法则主要分析EEG波形的几何性质，如幅度、均值、方差、偏歪度、峭度等。

这类方法主要是利用EEG波形的性质，如波幅、均值、方差、偏歪度和峭度等对临床EEG记录进行观察分析。在EEG信号研究中，常用的时域分析方法有：过零点分析、直方图分析、方差分析、相关分析、峰值检测、波形参数分析和波形识别等。

常使用的特征提取方法：

自回归(auto regressive, AR)、傅里叶变换(Fourier transform,FT)、表面拉普拉斯(surface-Laplacian)变换和小波变换(Wavelet transform,WT)

5不同特征提取方法特点

5.1快速傅里叶变换(Fast Fourier transform, FFT)

经典的FFT在分析确定信号和平稳信号时很有效，但在分析突变信号的频谱时具有一定的局限性。

对于alpha波、beta波等脑电基本节律，功率谱分析或FFT等方法可以从频域中直接提取出特征。

5.2稀疏傅里叶变换(Sparse Fourier transform, SFT)

SFT是时间窗内信号特征的平均，时间窗里信号越短，获得的时间分辨率就越高。该方法在一定程度上克服了FFT不具有的局部分析能力的缺陷，在某些信号处理中有一定的作用。

5.3自适应自回归(Adaptive Auto Regressive ,AAR)

AAR模型参数方法随每一样本点的输入而改变，能够很好地反映大脑的状态。不过，该方法更适合分析平稳的脑电信号，对包含高度非平稳信号的运动想象EEG，该模型是有局限性的。

5.4小波变换(Wavelettransform, WT)

小波变换在低频时的时间分辨率较低，而频率分辨率较高；在高频时的时间分辨率较高，而频率分辨率较低，正符合低频信号变化緩慢而高频信号变化较快的特点。因此小波分析比傅里叶变换和短时傅里叶变换更适合分析非平稳的脑电信号。

参考：

从经典谱估计到现代谱估计_百度知道

信号频域分析方法的理解（频谱、能量谱、功率谱、倒频谱、小波分析） - 知乎

采样频率、采样点数、频率分辨率

科学网—傅里叶变换的波形分辨率与频率分辨率 - 彭真明的博文

FFT补零可以提高频率分辨率吗？_不积跬步，无以至千里-CSDN博客_补零可以提高频率分辨率吗

快速傅里叶变换(FFT)中为什么要“补零”？ - 知乎

FFT Zero Padding - BitWeenie | BitWeenie

Zero Padding Theorem (Spectral Interpolation)

AR模型在信号处理中的应用_傅斯年的写字台-CSDN博客