AI算法工程师 | 07机器学习-无监督学习(一)聚类系列算法
文章目录
- 前言
- 导图 - 文章框架
- 机器学习 - 无监督学习 之 聚类系列算法
-
- 一、聚类的基本介绍
-
- 1. 了解聚类任务
- 2. 聚类算法
- 3. 相似度 与 数据间的相似度
- 4. 欧氏距离测度 与 余弦距离测度
- 二、K-Means 聚类
-
- 1. K-Means 算法具体流程
- 2. K-Means 的特点
- 3. K-Means 的损失函数
- 4. K-Means 算法 K 的选择
- 三、K-Means 的变形
-
- 1. K-Medoids
- 2. 二分 K-Means
- 3. K-Means++
- 4. Mini Batch K-Means
- 5. Canopy 聚类
- 6. K-Means 代码测试不同情况下的聚类效果
- 四、层次聚类
-
- 1. 分裂法
- 2. 凝聚法
- 五、密度聚类
-
- 1. DBSCAN 密度聚类算法
- 2. 基于 sklearn 的密度聚类代码
- 六、谱聚类(了解即可)
-
- 1. 构图
- 2. 切图
- 3. 基于 sklearn 的谱聚类代码
前言
本阶段将开启 无监督机器学习 的旅程。对于无监督机器学习问题,主要有两种:聚类、降维
聚类 Clustering
- 本质:根据样本和样本之间的相似度归堆
- 目标:将一批数据划分到多个组
- 应用:用户分组、异常检测、前景背景分离
降维 Dimensionality Reduction
- 本质:去掉冗余信息量或噪声
- 目标:将数据的维度减少
- 应用:数据的预处理、可视化、提高模型计算速度
小贴士:
① 聚类就是分组(归堆);降维类似于换个角度去审视原来的数据。
② 由于维度越多,速度越慢。所以,为提高模型运行速度,通常会做降维的任务。
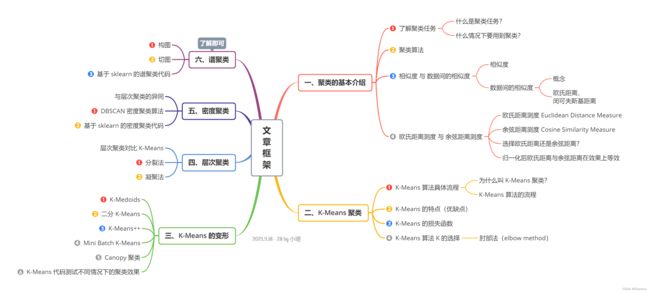
导图 - 文章框架
机器学习 - 无监督学习 之 聚类系列算法
一、聚类的基本介绍
1. 了解聚类任务
- 属于:无监督机器学习的一种
- 目标:将已有数据根据相似度划分到不同的簇(组) custer
- 待达到的效果:簇内样本彼此之间越相似,不同簇的样本之间越不相似,就越好(即:尽可能让组内的相似程度大,组与组之间的相似程度小)
什么情况下要用到聚类?
- 希望把已知的无标签的数据,划分到不同组中时,可用聚类任务去做
- 聚类不仅仅可以把已知的数据划分到组中,对未来数据也可进行预测
- 通过聚类,做异常检测(如:设置一个阈值 Threshold,若某样本点到所有中心点的距离都比阈值大,则该样本点为异常点)
2. 聚类算法
从图中可以看出,不同的聚类算法,对于不同的数据分布场景,其聚类效果有所不同。
本文将针对 K-Means 聚类、层次聚类、密度聚类以及谱聚类展开介绍。
小贴士
- scikit-learn:是针对 Python 编程语言的免费软件机器学习库
- 关于 scikit-learn 的社区地址:外语:scikit-learn.org; 中文:scikit-learn.org.cn
3. 相似度 与 数据间的相似度
3.1 相似度
对于相似度的判断,站在不同的角度会有不同的结果:
- 不同测量相似度的方式,会得到不同的结果
- 不同提特征的方式(即:注意力不同),结果不同
- 计算方式不同,相似度也不同
举例:
- 看图说话 image caption
3.2 数据间的相似度
概念:
- 每一条数据都可以理解为多维空间中的一个点
- 可以根据点和点之间的距离来评价数据间的相似度
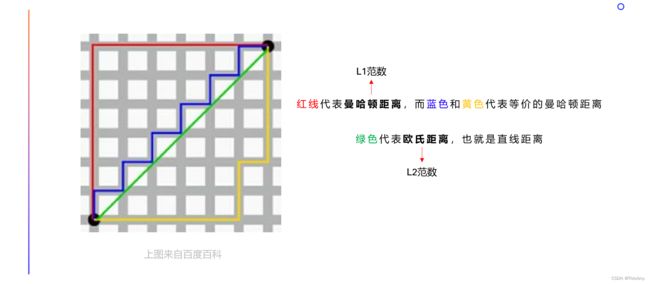
欧氏距离、闵mǐn可夫斯基距离:
小贴士
- 这些距离可用 “向量的范数” 进行表示,感兴趣的伙伴可阅读:04人工智能基础-高等数学知识强化(三)线性代数基础之向量 —— 文中的 “向量到原点的范式” 部分
4. 欧氏距离测度 与 余弦距离测度
如何计算样本到中心点的距离?通常有两种方式:① 欧氏距离测度、② 余弦距离测度
4.1 欧氏距离测度 Euclidean Distance Measure
公式:(也就是上文中的欧式距离)
e u c l i d e a n ( A , B ) = ∑ i = 1 n ( A i − B i ) 2 euclidean(A,B)=\sqrt{\sum_{i=1}^{n}(A_i -B_i)^{2}} euclidean(A,B)=i=1∑n(Ai−Bi)2
说明:欧氏距离越大,相似度越低
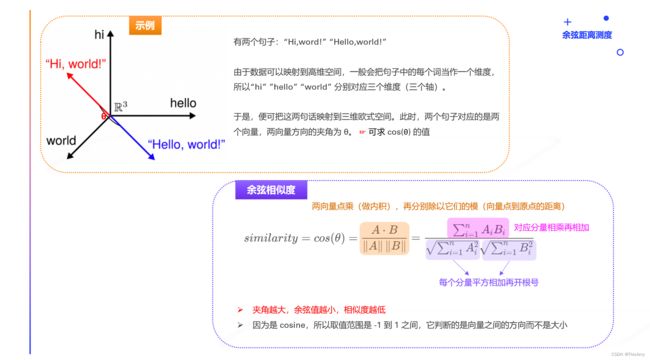
4.2 余弦距离测度 Cosine Similarity Measure
步骤:
- 将数据映射为高维空间中的点(向量)
- 计算向量间的余弦值
- 余弦相似度的取值范围 [-1,+ 1],它判断的是向量之间的方向而不是大小
- 越趋近于 1 代表越相似(两向量方向相同),越趋近于 -1 代表方向相反,0 代表正交(两向量方向相对成90°)
公式:(余弦相似度)
s i m i l a r i t y = c o s ( θ ) = A ⋅ B ∥ A ∥ ∥ B ∥ = ∑ i = 1 n A i B i ∑ i = 1 n A i 2 ∑ i = 1 n B i 2 similarity = cos(\theta) = \frac{A\cdot B}{\left \| A \right \|\left \| B \right \|} = \frac{\sum_{i=1}^{n}A_iB_i}{\sqrt{\sum_{i=1}^{n}A_i^{2}}\sqrt{\sum_{i=1}^{n}B_i^{2}}} similarity=cos(θ)=∥A∥∥B∥A⋅B=∑i=1nAi2∑i=1nBi2∑i=1nAiBi
说明:夹角越大,余弦值越小,相似度越低
小贴士
- 余弦距离 = 1 - 余弦相似度
- ∴ 余弦距离的取值范围:[0, 2]
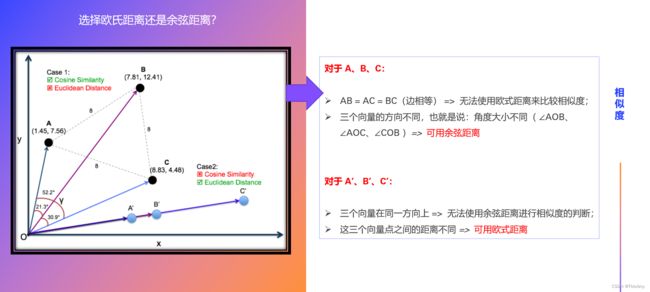
4.3 选择欧氏距离还是余弦距离?
总结:
- 欧氏距离:体现数值上的绝对差异;
- 余弦距离:体现方向上的相对差异。
举例:
- 示例1:统计两部剧的用户观看行为
- 假设用户 A 的观看向量为(0,1),用户 B 为(1,0);
- 此时二者的余弦距离很大,而欧氏距离很小;
- 我们分析两个用户对于不同视频的偏好,更关注相对差异,显然应当使用余弦距离。
- 示例2:分析用户活跃度
- 当以登陆次数(单位:次)和平均观看时长(单位:分钟)作为特征时,
- 余弦距离会认为(1,10)、(10,100)两个用户距离很近;
- 但显然这两个用户活跃度是有着极大差异的,此时我们更关注数值绝对差异,应当使用欧氏距离。
小贴士
- 欧氏距离测度是常用的距离测度
- 余弦距离测度更适用于文本:余弦相似度可以评价文章的相似度,从而实现对文章,进行分类
4.4 归一化后欧氏距离与余弦距离在效果上等效
概述:
- 如果向量的模长是经过归一化的,可以理解为此时向量被投影到了一个长度为 1 的球面上
- 这时欧氏距离和余弦距离有着单调的关系,即
∣ ∣ A ∥ A ∥ − B ∥ B ∥ ∣ ∣ 2 = 2 ∗ ( 1 − c o s ( A , B ) ) ||\frac{A}{\begin{Vmatrix}A\end{Vmatrix}}-\frac{B}{\begin{Vmatrix}B\end{Vmatrix}}||_2=\sqrt{2∗(1-cos(A,B))} ∣∣∥ ∥A∥ ∥A−∥ ∥B∥ ∥B∣∣2=2∗(1−cos(A,B))
推导:
说明:
- 在向量的模长归一化的场景下,谁距离最小(相似度最大)就是近邻,那么使用余弦相似度和欧氏距离的查找近邻结果是相同的。
小贴士
- 参考:余弦相似度和余弦距离的推导与理解
二、K-Means 聚类
❥ K-Means 聚类属于聚类任务的算法之一
1. K-Means 算法具体流程
为什么叫 K-Means 聚类?
- 也叫:K均值聚类
- K:是最终簇数量(即:K 往往代表类别的个数),它是超参数,需要预先设定
- 在算法计算中会涉及到求均值
- 随机选择 K 个簇中心点(可以选已有的数据作为中心点,也可直接选高维空间中的位置)
- 样本被分配到离其最近的中心点
- K 个簇中心点根据所在簇样本,以求平均值的方式重新计算
- 开始迭代,重复第2步和第3步直到所有样本的分配不再改变
K-Means 必须首先知道要分为几个组(即:K 需要预先设定)
假设 K = 3,这三个类别的位置,开始是不知道的:
- 随机选择三个样本点,作为三个类别的初始中心点
- 通过机器学习算法,不断的迭代,逼近最优结果
- 迭代:求样本点分别距离这三个中心点的距离,把各样本归入距离中心点最近的那组
问:K-Means 要干的事情是什么?
答:求平均
- 每个样本点相加 除以 组中样本个数 → 得到中心位置
- 当中心点位置变了时,各样本点到中心点的距离便会变,需再次求平均
- 以此往复,直到中心点位置不变 → 即:收敛了
问:迭代终止条件是什么?
答:没有新的样本点被划分进某组(即:所有样本的分配不再改变;也可以理解为:中心点的位置不再变化)
2. K-Means 的特点
优点:
- 简单,效果不错(对于大部分数据集而言)
缺点:
- 对异常值敏感(若有异常值,无论划分到哪个组,均会影响该组内的平均值计算)
- 对初始值敏感(若随机的中心点距离较近,多次得到的结果极可能不同,可能是局部最优解)
- K-Means 算法不保证找到最好的解(即:不保证收敛全局最优)
- 通常的做法:运行 K-Means 很多次,每次随机初始化不同的初始中心点,然后从多次运行结果中选择最好的局部最优解
- 对某些分布聚类效果不好(如:当样本的方差不相等时聚类效果不好)
3. K-Means 的损失函数
目标函数
- 聚类问题的损失函数:求各个样本点到对应簇的中心点的误差平方和
小贴士
- 参考1:K-Means算法详细介绍(SSE、轮廓分析)
- 参考2:参数误差统计:SSE、SSR、SST、R_square、MSE、RMSE
4. K-Means 算法 K 的选择
对于聚类数 K 的选择,其中一种方式便是肘部法(elbow method)
肘部法
目标:(找到最合适的点——拐点)
- 找到一个 K,使得高于该值之后的收益会发生递减;
- 这个 K 值,称为肘部点(elbow point),因为它看起来像一个人的肘部。
如何判断拐点?
- 求幅度差(收益 gain),找收益最大的点(如上图所示),也就是一开始下降最快的点
动图-演示:
小贴士
- 没有所谓最好的选择聚类数的方法,通常是需要根据不同的问题,人工进行选择的。
三、K-Means 的变形
下面介绍一些由 K-Means 所衍生出来的算法,它们针对 K-Means 所暴露出来的不足进行了优化,如:① K-Medoids、② 二分 K-Means、③ K-Means++、④ Mini-batch Kmeans 算法等
| 算法 | 针对 K-Means 中的不足点 | 优化内容 |
|---|---|---|
| K-Medoids | K-Means 算法对异常值很敏感 | 从求平均切换为求中位数 |
| 二分 K-Means | K-Means 算法的初始中心点位置,很大程度上会影响聚类的效果 | 再次划分,重新改变中心点位置 |
| K-Means++ | K-Means 选择一个好的初始中心非常重要,初始中心点分布不够均匀往往会导致聚类效果不好 | 改进了 K-Means 算法初始中心点的方式 |
| Mini Batch K-Means | K-Means 算法中需要计算所有样本点到所有质心的距离,计算复杂度较高 | 随机选择一部分的数据求均值 |
本节还会介绍一个 Canopy 聚类算法,虽然不是 K-Means 所衍生出来的算法,但它很少单独使用,会结合 K-Means 一起使用。
1. K-Medoids
- 计算新的簇中心的时候不再选择均值,而是选择中位数
- 抗噪能力得到加强
说明:
- 若为中位数,每次得到的点一定是某个样本
- K-Medoids 主要针对解决噪音和异常点比较敏感问题
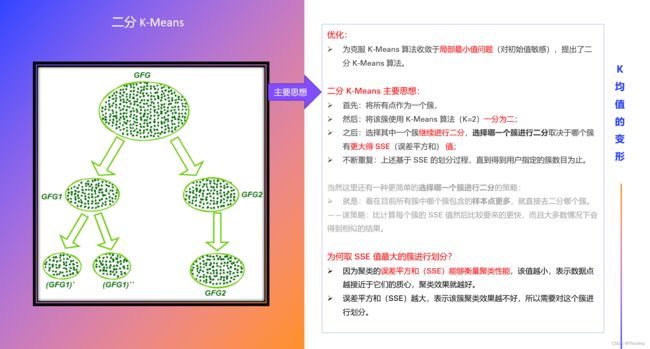
2. 二分 K-Means
步骤:
- ① 将所有点作为一个簇;
- ② 将该簇使用 K-Means 算法(K=2)一分为二;
- ③ 选择其中一个簇继续进行二分,选择哪一个簇进行二分取决于哪个簇有更大得 SSE(误差平方和) 值;
- ④ 不断重复第③步,直到得到用户指定的簇数目 K 为止。
小贴士
- 参考:机器学习 K-Means 方面的算法
3. K-Means++
优化:
- 若 K-Means 的初始中心点分布不够均匀,往往会导致聚类效果不好;
- 为了克服上面的缺点,K-Means++ 通过一个更聪明的初始化中心点方法(通过概率化选择初始中心点)确保改进聚类的质量。
- 除了初始化,该算法其它和标准的 K-Means 算法一样
- 所以,K-Means++ 相当于 => 标准的 K-Means 算法 + 一个更好的初始化中心点的方法
目标:
- 初始化簇中心点稍微远一些
初始化中心点的步骤:
- ① 从数据集中随机选择第一个中心点
- ② 对于每个数据点(样本)计算到它最近邻的已知中心点的距离
- ③ 将距离转化为概率,进行概率化选择:从数据集中选择下一个中心点,是一个概率化选择,被选择的概率和上一步计算出来的距离成正比
- 例如:某个点到最近邻的已知中心点距离最远,它有最大的可能性被选为下一个中心点
- ④ 重复第②步和第③步直到 K 个中心点被采样
K-Means++ 用到的范围比较广,如:
- sklean(全称 Scikit-Learn)中默认使用的便是 K-Means++;
- Spark(分布式计算框架)中 MLlib 模块 默认的 K-Means 也是 K-Means++。
小贴士:K-Means++ 的初始化中心点
- K-Means++ 是一个一个中心点依次选取出来的
- 概率化选择时,其概率为均匀分布,在(0,1)间随机取值,由于将距离转化为概率,而距离远的其在数轴中的长度间隔会更大,所以更有可能被选中
4. Mini Batch K-Means
该算法的迭代步骤有两步:
- ① 从数据集中随机抽取一些数据形成小批量,把他们分配给最近的质心
- ② 更新质心
区别:
- 与 K 均值算法相比,Mini Batch K-Means 数据的更新是在每一个小的样本集上。
- 对于每一个小批量,通过计算平均值得到更新质心,并把小批量里的数据分配给该质心,
- 随着迭代次数的增加,这些质心的变化是逐渐减小的,
- 直到质心稳定或达到指定的迭代次数,停止计算。
5. Canopy 聚类
特点:一次迭代,出 k 个中心点的结果
Canopy 聚类的步骤:
- 设置两个距离 T1 T2,作为超参数;其中 T1>T2
- WHILE D 非空∶( D 为所有点的集合,不断遍历 D,直至所有点都被划分到某簇的 T2 内或成为某簇中心,也就是 D 为空 )
- 随机产生 d 属于 D,作为中心点
- 计算所有点到 d 的距离
- 所有距离
- 从 D 中删除 d 及距离小于 T2 的点(删除的这些点不能作为其他簇的中心,D 中剩余的点进行重复前面的操作)
Canopy 聚类的说明:
- Canopy 聚类很少单独使用,会结合 K-Means 一起使用
- Canopy 聚类 可以作为 K-Means 中第一步初始中心点的选择
- 即:K-Means 中的随机中心值 → 变为使用 Canopy 聚类获得中心值
- 该聚类一定会把样本划分到某个簇中,且很可能一个样本属于多个类别
- 与 K-Means++ 类似,其中心点是一个一个找出来的,处理第一个中心点是随机的
K-Means 在初始中心点时,使用 Canopy 聚类的好处:
- 可以帮助我们得出 k 为多少
- 能让中心点尽可能远离些
小贴士
- 参考1:Canopy 聚类、层次聚类、密度聚类-DBSCAN
- 参考2:Canopy 聚类算法分析
6. K-Means 代码测试不同情况下的聚类效果
下面是基于 sklearn 库做的聚类,使用的算法为 K-Means++
代码:( 工具:PyCharm,基于:python3)
各步骤说明:
- 导入模块
import numpy as np
import matplotlib.pyplot as plt
import sklearn.datasets as ds # 通过datasets,帮我们创建一些数据集
import matplotlib.colors # 关于颜色的
from sklearn.cluster import KMeans # k-means 聚类
- 数据准备
N = 400 # 一共想创建400个数据(样本)
centers = 4 # 告诉函数,要创建4个组(共4个中心点)
# -----下面创建了三组不同的数据,1、第一组:根据高斯分布,创建同方差的数据(400样本,4个组,每组100个);2、第二组:高斯分布的方差不同;3、第三组:同方差,但只选择了175条数据(且各组数据个数不同) ------
# make_blobs 创建数据,括号中的参数:① 创建多少样本,② 每条样本的维度(这里:400行2列),③ 样本分到多少个组中,④ 创建随机种子
data, y = ds.make_blobs(N, n_features=2, centers=centers, random_state=2) # 得到每组中的数据data 及 label标签y(每个样本在哪个组)
# 此处多了个 cluster_std —— 每组对应的方差(此处设置成了不同的),上面那条代码默认同方差的
data2, y2 = ds.make_blobs(N, n_features=2, centers=centers, cluster_std=(1, 2.5, 0.5, 2), random_state=2)
# vstack:竖的堆叠,括号中个参数含义:① 将标签y为0的该组中,所有数据取出(100条);② 组别为1的样本,只取50条;③ 组别为2的样本,只取20条;④ 3的:5条
data3 = np.vstack((data[y == 0][:], data[y == 1][:50], data[y == 2][:20], data[y == 3][:5]))
# 这里的 标签y 需要自己写。说明:[0] * 100 这种 —— 是原生的python - 将列表扩展,得:一个列表中有100个0; 加号代表:将列表元素拼在一起
# 下列代码结果:用列表装数据,前100个为0,50个1,20个2,最后5个为3
y3 = np.array([0] * 100 + [1] * 50 + [2] * 20 + [3] * 5)
- K-Means++ 聚类(核心代码)
# ----- K-means++ 算法 (核心代码:调用 k-means++ 训练和预测,得到相应的 ŷ 结果)-----
cls = KMeans(n_clusters=4, init='k-means++') # 创建k-means对象,括号中参数:① n_clusters:指定K的个数;② init:初始化 k-means 算法的超参数=
y_hat = cls.fit_predict(data) # 对对象进行聚类,得到聚类的结果(fit_predict 返回的是:数据的类别号)
y2_hat = cls.fit_predict(data2)
y3_hat = cls.fit_predict(data3)
# 下面:通过矩阵,将原来的数据做了高维空间的线性变换,将其映射到新的维度中(相当于 做了旋转)
m = np.array(((1, 1), (1, 3))) # 把元组变为了2行2列的矩阵。矩阵能干的事情:高维空间的线性变换
data_r = data.dot(m) # 点乘:用 原始数据data 点乘 矩阵m → 相当于 把数据中的每个向量点,全部进行相对于的旋转,投影到另外一个轴中
y_r_hat = cls.fit_predict(data_r)
- 可视化展示
def expand(a, b): # 后续画图时会用到的自定义函数
d = (b - a) * 0.1
return a - d, b + d
# ----- 以下是画图的内容,共画了8个子图 ------------------------------
matplotlib.rcParams['font.sans-serif'] = [u'SimHei'] # 可展示中文(黑体)
matplotlib.rcParams['axes.unicode_minus'] = False # 让负号可以正常显示
cm = matplotlib.colors.ListedColormap(list('rgbm'))
plt.figure(figsize=(9, 10), facecolor='w')
plt.subplot(421) # 8个子图中的:第一个子图
plt.title(u'原始数据') # u:表示unicode字符串
plt.scatter(data[:, 0], data[:, 1], c=y, s=30, cmap=cm, edgecolors='none') # 散点图,传真实结果 y
x1_min, x2_min = np.min(data, axis=0)
x1_max, x2_max = np.max(data, axis=0)
x1_min, x1_max = expand(x1_min, x1_max)
x2_min, x2_max = expand(x2_min, x2_max)
plt.xlim((x1_min, x1_max)) # x 轴
plt.ylim((x2_min, x2_max)) # y 轴
plt.grid(True) # 网格
plt.subplot(422)
plt.title(u'KMeans++聚类')
plt.scatter(data[:, 0], data[:, 1], c=y_hat, s=30, cmap=cm, edgecolors='none') # 散点图,传预测结果 ŷ
plt.xlim((x1_min, x1_max))
plt.ylim((x2_min, x2_max))
plt.grid(True)
plt.subplot(423)
plt.title(u'旋转后数据')
plt.scatter(data_r[:, 0], data_r[:, 1], c=y, s=30, cmap=cm, edgecolors='none')
x1_min, x2_min = np.min(data_r, axis=0)
x1_max, x2_max = np.max(data_r, axis=0)
x1_min, x1_max = expand(x1_min, x1_max)
x2_min, x2_max = expand(x2_min, x2_max)
plt.xlim((x1_min, x1_max))
plt.ylim((x2_min, x2_max))
plt.grid(True)
plt.subplot(424)
plt.title(u'旋转后KMeans++聚类')
plt.scatter(data_r[:, 0], data_r[:, 1], c=y_r_hat, s=30, cmap=cm, edgecolors='none')
plt.xlim((x1_min, x1_max))
plt.ylim((x2_min, x2_max))
plt.grid(True)
plt.subplot(425)
plt.title(u'方差不相等数据')
plt.scatter(data2[:, 0], data2[:, 1], c=y2, s=30, cmap=cm, edgecolors='none')
x1_min, x2_min = np.min(data2, axis=0)
x1_max, x2_max = np.max(data2, axis=0)
x1_min, x1_max = expand(x1_min, x1_max)
x2_min, x2_max = expand(x2_min, x2_max)
plt.xlim((x1_min, x1_max))
plt.ylim((x2_min, x2_max))
plt.grid(True)
plt.subplot(426)
plt.title(u'方差不相等KMeans++聚类')
plt.scatter(data2[:, 0], data2[:, 1], c=y2_hat, s=30, cmap=cm, edgecolors='none')
plt.xlim((x1_min, x1_max))
plt.ylim((x2_min, x2_max))
plt.grid(True)
plt.subplot(427)
plt.title(u'数量不相等数据')
plt.scatter(data3[:, 0], data3[:, 1], s=30, c=y3, cmap=cm, edgecolors='none')
x1_min, x2_min = np.min(data3, axis=0)
x1_max, x2_max = np.max(data3, axis=0)
x1_min, x1_max = expand(x1_min, x1_max)
x2_min, x2_max = expand(x2_min, x2_max)
plt.xlim((x1_min, x1_max))
plt.ylim((x2_min, x2_max))
plt.grid(True)
plt.subplot(428)
plt.title(u'数量不相等KMeans++聚类')
plt.scatter(data3[:, 0], data3[:, 1], c=y3_hat, s=30, cmap=cm, edgecolors='none')
plt.xlim((x1_min, x1_max))
plt.ylim((x2_min, x2_max))
plt.grid(True)
plt.suptitle(u'数据分布对KMeans聚类的影响', fontsize=18) # 总标题
plt.tight_layout() # 会自动调整子图参数,使之填充整个图像区域(防止重叠)
plt.savefig('cluster_kmeans') # 将绘图结果保存为png图片
plt.show() # 展示
小贴士
- 若对于 python 中 matplotlib 绘图不太了解的伙伴,可参考文章:AI算法工程师 | 03人工智能基础-Python科学计算和可视化(二)Matplotlib
整体代码:
# !/usr/bin/python
# -*- coding:utf-8 -*-
"""
基于 sklearn 库做聚类:K-Means++
"""
# 导入包
import numpy as np
import matplotlib.pyplot as plt
import sklearn.datasets as ds # 通过datasets,帮我们创建一些数据集
import matplotlib.colors # 关于颜色的
from sklearn.cluster import KMeans # k-means 聚类
def expand(a, b):
d = (b - a) * 0.1
return a - d, b + d
if __name__ == "__main__":
N = 400 # 一共想创建400个数据(样本)
centers = 4 # 告诉函数,要创建4个组(共4个中心点)
# -----下面创建了三组不同的数据,1、第一组:根据高斯分布,创建同方差的数据(400样本,4个组,每组100个);2、第二组:高斯分布的方差不同;3、第三组:同方差,但只选择了175条数据(且各组数据个数不同) ------
# make_blobs 创建数据,括号中的参数:① 创建多少样本,② 每条样本的维度(这里:400行2列),③ 样本分到多少个组中,④ 创建随机种子
data, y = ds.make_blobs(N, n_features=2, centers=centers, random_state=2) # 得到每组中的数据data 及 label标签y(每个样本在哪个组)
# 此处多了个 cluster_std —— 每组对应的方差(此处设置成了不同的),上面那条代码默认同方差的
data2, y2 = ds.make_blobs(N, n_features=2, centers=centers, cluster_std=(1, 2.5, 0.5, 2), random_state=2)
# vstack:竖的堆叠,括号中个参数含义:① 将标签y为0的该组中,所有数据取出(100条);② 组别为1的样本,只取50条;③ 组别为2的样本,只取20条;④ 3的:5条
data3 = np.vstack((data[y == 0][:], data[y == 1][:50], data[y == 2][:20], data[y == 3][:5]))
# 这里的 标签y 需要自己写。说明:[0] * 100 这种 —— 是原生的python - 将列表扩展,得:一个列表中有100个0; 加号代表:将列表元素拼在一起
# 下列代码结果:用列表装数据,前100个为0,50个1,20个2,最后5个为3
y3 = np.array([0] * 100 + [1] * 50 + [2] * 20 + [3] * 5)
# ----- K-means 算法 (核心代码:调用 k-means 训练和预测,得到相应的 ŷ 结果)-----
cls = KMeans(n_clusters=4, init='k-means++') # 创建k-means对象,括号中参数:① n_clusters:指定K的个数;② init:初始化 k-means 算法的超参数
y_hat = cls.fit_predict(data) # 对对象进行聚类,得到聚类的结果(fit_predict 返回的是:数据的类别号)
y2_hat = cls.fit_predict(data2)
y3_hat = cls.fit_predict(data3)
# 下面:通过矩阵,将原来的数据做了高维空间的线性变换,将其映射到新的维度中(相当于 做了旋转)
m = np.array(((1, 1), (1, 3))) # 把元组变为了2行2列的矩阵。矩阵能干的事情:高维空间的线性变换
data_r = data.dot(m) # 点乘:用 原始数据data 点乘 矩阵m → 相当于 把数据中的每个向量点,全部进行相对于的旋转,投影到另外一个轴中
y_r_hat = cls.fit_predict(data_r)
# ----- 以下是画图的内容,共画了8个子图 ------------------------------
matplotlib.rcParams['font.sans-serif'] = [u'SimHei'] # 可展示中文(黑体)
matplotlib.rcParams['axes.unicode_minus'] = False # 让负号可以正常显示
cm = matplotlib.colors.ListedColormap(list('rgbm'))
plt.figure(figsize=(9, 10), facecolor='w')
plt.subplot(421) # 8个子图中的:第一个子图
plt.title(u'原始数据') # u:表示unicode字符串
plt.scatter(data[:, 0], data[:, 1], c=y, s=30, cmap=cm, edgecolors='none') # 散点图,传真实结果 y
x1_min, x2_min = np.min(data, axis=0)
x1_max, x2_max = np.max(data, axis=0)
x1_min, x1_max = expand(x1_min, x1_max)
x2_min, x2_max = expand(x2_min, x2_max)
plt.xlim((x1_min, x1_max)) # x 轴
plt.ylim((x2_min, x2_max)) # y 轴
plt.grid(True) # 网格
plt.subplot(422)
plt.title(u'KMeans++聚类')
plt.scatter(data[:, 0], data[:, 1], c=y_hat, s=30, cmap=cm, edgecolors='none') # 散点图,传预测结果 ŷ
plt.xlim((x1_min, x1_max))
plt.ylim((x2_min, x2_max))
plt.grid(True)
plt.subplot(423)
plt.title(u'旋转后数据')
plt.scatter(data_r[:, 0], data_r[:, 1], c=y, s=30, cmap=cm, edgecolors='none')
x1_min, x2_min = np.min(data_r, axis=0)
x1_max, x2_max = np.max(data_r, axis=0)
x1_min, x1_max = expand(x1_min, x1_max)
x2_min, x2_max = expand(x2_min, x2_max)
plt.xlim((x1_min, x1_max))
plt.ylim((x2_min, x2_max))
plt.grid(True)
plt.subplot(424)
plt.title(u'旋转后KMeans++聚类')
plt.scatter(data_r[:, 0], data_r[:, 1], c=y_r_hat, s=30, cmap=cm, edgecolors='none')
plt.xlim((x1_min, x1_max))
plt.ylim((x2_min, x2_max))
plt.grid(True)
plt.subplot(425)
plt.title(u'方差不相等数据')
plt.scatter(data2[:, 0], data2[:, 1], c=y2, s=30, cmap=cm, edgecolors='none')
x1_min, x2_min = np.min(data2, axis=0)
x1_max, x2_max = np.max(data2, axis=0)
x1_min, x1_max = expand(x1_min, x1_max)
x2_min, x2_max = expand(x2_min, x2_max)
plt.xlim((x1_min, x1_max))
plt.ylim((x2_min, x2_max))
plt.grid(True)
plt.subplot(426)
plt.title(u'方差不相等KMeans++聚类')
plt.scatter(data2[:, 0], data2[:, 1], c=y2_hat, s=30, cmap=cm, edgecolors='none')
plt.xlim((x1_min, x1_max))
plt.ylim((x2_min, x2_max))
plt.grid(True)
plt.subplot(427)
plt.title(u'数量不相等数据')
plt.scatter(data3[:, 0], data3[:, 1], s=30, c=y3, cmap=cm, edgecolors='none')
x1_min, x2_min = np.min(data3, axis=0)
x1_max, x2_max = np.max(data3, axis=0)
x1_min, x1_max = expand(x1_min, x1_max)
x2_min, x2_max = expand(x2_min, x2_max)
plt.xlim((x1_min, x1_max))
plt.ylim((x2_min, x2_max))
plt.grid(True)
plt.subplot(428)
plt.title(u'数量不相等KMeans++聚类')
plt.scatter(data3[:, 0], data3[:, 1], c=y3_hat, s=30, cmap=cm, edgecolors='none')
plt.xlim((x1_min, x1_max))
plt.ylim((x2_min, x2_max))
plt.grid(True)
plt.suptitle(u'数据分布对KMeans聚类的影响', fontsize=18) # 总标题
plt.tight_layout() # 会自动调整子图参数,使之填充整个图像区域(防止重叠)
plt.savefig('cluster_kmeans') # 将绘图结果保存为png图片
plt.show() # 展示
结果展示:
四、层次聚类
层次聚类解决了 K-Means 中 K 值选择和初始中心点选择的问题。
其聚类方式分为:① 分裂法、② 凝聚法
层次聚类对比 K-Means:
- K-Means 这种扁平聚类产出一个聚类结果(都是独立的)
- 层次聚类能够根据你的聚类程度不同,有不同的结果
- K-Means 需要指定聚类个数 K,层次聚类不用(可以根据距离的远近设置阈值,达到该阈值时不再分裂/合并)
- K-Means 比层次聚类要快一些(通常说来)
- K-Means(K-均值聚类)用的多,有些时候可以用 K-Median(K-中值聚类)
1. 分裂法
像一棵树一样,不断的分裂
算法步骤:
- 将所有样本归为一个簇
- While 不足 k 个簇或距离阈值(距离阈值作用:表示相似度):
- 在同一个簇 C 中计算样本间距离,选最远的距离的两个样本 a、b(终止条件检测)
- 将样本 a, b 划入 C1、C2(终止条件检测)
- 计算原簇 C 中样本离谁近,划入谁
说明:二分 K-Means 本质上是层次聚类中的分裂法,它通过不断分裂直到达到预设的簇类个数。
2. 凝聚法
原理:
- 最初将每个对象看成一个簇,
- 然后将这些簇根据某种规则被一步步合并,
- 就这样不断合并直到达到预设的簇类个数。
算法步骤:
- 将所有点看做一个独立的簇
- While 多于 k 个簇或距离阈值︰
- 计算两两簇之间的距离(关键:如何计算聚类簇之间的距离?),找到最小距离的簇 C1 和 C2(多种计算方式,如:欧式距离与余弦距离算出来的不一样)
- 合并 C1、C2
合并 C1、C2 的方式可以有所差别︰(两个簇之间距离的度量)
- 两个簇间距离最小的样本距离
- 两个簇间最远的两个点的距离
- 两个簇之间两两求距离的平均值
- 两个簇之间两两求距离的中位数
- 求每个集合的中心点,用中心点的距离代表簇的距离
五、密度聚类
与层次聚类的异同:
-
同:与层次聚类一样无需设置 K 值
-
异:
- 层次聚类:有包含关系;算的是距离;
- 密度聚类:无包含关系;算的是密度。
密度聚类最参见的算法为:DBSCAN 算法
1. DBSCAN 密度聚类算法
概述:
- DBSCAN ( Density-Based Spatial Clustering of Applications
with Noise) - 一个基于密度聚类的算法。它将簇定义为密度相连的点的最大集合,能够把具有高密度的区域划分为簇,并可有效地对抗噪声
什么叫密度相连?
先来了解几个概念:
- 对象的 ε ε ε 邻域: 给定对象(某个点)在半径 ε ε ε 内的区域;
- 核心对象: 给定一个数目 m m m, 如果对象(某个点)的 ε ε ε 领域内, 至少含有 m m m个对象(点), 该对象就是核心对象;
- 白话:在样本点中间被包围的点,比较具有代表性,是核心对象
- 直接密度可达: 给定一个对象集合 D D D, 如果 p p p 在 q q q 的 ε ε ε 邻域内,而 q q q 是一个核心对象, p p p 从 q q q 出发是直接密度可达的;
- 白话: 直接密度可达就是他俩直接够得着
- 密度可达:它是在直接密度可达的基础上的。如果存在一个对象链 p 1 p 2 . . . p n p_1p_2... p_n p1p2...pn ,令 p 1 = p , p n = q , p i + 1 p_1=p,p_n=q,p_{i+1} p1=p,pn=q,pi+1 是关于 ε 、 m ε、m ε、m是直接密度可达的, 那么对象 p p p 是从对象 q q q 关于 ε 、 m ε 、m ε、m 密度可达的;
- 即:密度可达满足传递性(对于核心对象而言),但不满足对称性
- 密度相连:它是在密度可达的基础之上的。如果集合 D D D 中存在一个对象 o o o,使 o → p o→p o→p 密度可达, o → q o→q o→q 密度可达,那么 p p p 和 q q q 就是关于 ε 、 m ε 、m ε、m 密度相连的。
- 即:密度相连满足对称性
从上述可知,密度聚类有两个超参数: ε ε ε 、 m m m
密度可达 和 密度相连有什么用?
- 密度可达:相关对象(点)划分到同一个簇
- 密度相连:也划分到同一个簇
算法步骤:
DBSCAN 通过检查数据集中每个对象的 ε ε ε 邻域来寻找聚类
步骤:(下面是更新一个簇的思路)
- 如果一个点 p p p 的 ε ε ε 邻域中多余 m m m 个对象,则创建一个 p p p 为核心对象的新簇;
- 依据 p p p 来反复寻找密度相连的集合(有可能合并原有已经生成的簇);
- 当没有任何新的点可以被添加到簇中的时候,寻找结束。
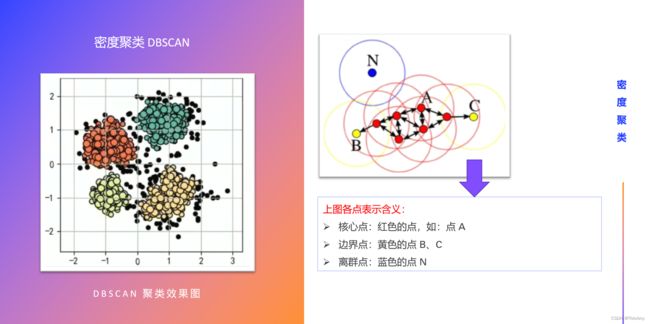
根据半径( ε ε ε 邻域)、最少点数( m m m )区分核心点、边界点、噪声点:
- 核心点:核心点的半径范围( ε ε ε 邻域))内的样本个数 ≥ m ≥m ≥m ;
- 每个簇至少包含一个核心点(核心对象)
- 边界点:边界点的半径范围内的样本个数 < m <m <m ,但 > 0 >0 >0;
- 非核心对象可以是簇的一部分,构成簇的边缘
- 噪声点:噪声点的半径范围的样本个数为 = 0 =0 =0。
- 包含过少对象的簇被认为是噪声
小贴士
- List item
- 参考1:密度聚类(DBSCAN / MDCA) by loveliuzz
- 参考2:六种常见聚类算法(参考的文中密度聚类部分) by TingXiao-Ul
2. 基于 sklearn 的密度聚类代码
下面是基于 sklearn 库做的聚类,感受超参数 ε ε ε 、 m m m 不同的情况 DBSCAN 聚类的效果
代码:( 工具:PyCharm,基于:python3)
# ----- 导入模块 -----
import numpy as np
import matplotlib.pyplot as plt
import sklearn.datasets as ds # 通过datasets,帮我们创建一些数据集
import matplotlib.colors # 关于颜色的
from sklearn.cluster import DBSCAN # 密度聚类
from sklearn.preprocessing import StandardScaler
def expand(a, b):
d = (b - a) * 0.1
return a - d, b + d
if __name__ == "__main__":
# ----- 数据准备 ----------------------
N = 1000
centers = [[1, 2], [-1, -1], [1, -1], [-1, 1]] # 指明簇中心的位置
# make_blobs 函数:生成数据集。—— 创建1000个样本点,每个样本点有2个特征,指定了4个簇中心,默认使用正态分布-随机初始化数据,random_state:为了保证程序每次运行都分割一样的训练集和测试集
data, y = ds.make_blobs(N, n_features=2, centers=centers, cluster_std=[0.5, 0.25, 0.7, 0.5], random_state=0)
data = StandardScaler().fit_transform(data) # 进行归一化
# 数据的参数:(epsilon, min_sample) —— 半径,最少的样本的个数。下面创建了六组超参数
params = ((0.2, 5), (0.2, 10), (0.2, 15), (0.3, 5), (0.3, 10), (0.3, 15))
# ----- 以下是画图的内容,画了6个子图(因为设置了 6 组超参数,每次循环取出一组进行密度聚类) ------------------------------
matplotlib.rcParams['font.sans-serif'] = [u'SimHei'] # 可展示中文(黑体)
matplotlib.rcParams['axes.unicode_minus'] = False # 让负号可以正常显示
plt.figure(figsize=(12, 8), facecolor='w') # 设置画布大小和颜色
plt.suptitle(u'DBSCAN聚类', fontsize=20) # 主标题
for i in range(6):
# ----- 下面进行密度聚类(核心代码)--------------
eps, min_samples = params[i] # 取出每组超参数
""" 调用 DBSCAN 密度聚类算法
参数含义:
· eps: 半径,表示以给定点 p 为中心的圆形部域的范围
· min_samples: 以点 p 为中心的邻域内最少点的数量
如果满足 以点 p 为中心,半径为 eps 的领域内,点的个数不少 min_samples ,则称点 p 为【核心点】
"""
model = DBSCAN(eps=eps, min_samples=min_samples) # DBSCAN 密度聚类算法
model.fit(data) # 训练 DBSCAN 模型
y_hat = model.labels_ # 拿到每个样本对应的类别聚类的结果。无论核心点还是边界点,只要是同一个簇的都被赋予同样的label,噪声点为-1.
core_indices = np.zeros_like(y_hat, dtype=bool) # 生成数据类型和形状和 y_hat 一致的初始化为0的数组。dtype=bool:会覆盖原数据类型,∴是一个布尔数组
core_indices[model.core_sample_indices_] = True # model.core_ sample_ 核心点的索引。由于labels_无法区分核心点与边界点,所以要用该索引确定核心点。
y_unique = np.unique(y_hat) # 统计总共有几类,其中为 -1 的:表示未分类样本。unique 函数:去除其中重复的元素
n_clusters = y_unique.size - (1 if -1 in y_hat else 0) # 得到聚类簇的个数
print(y_unique, '聚类簇的个数为:', n_clusters)
plt.subplot(2, 3, i + 1) # 共6张子图(2行3列),绘制第 i+1 张
clrs = plt.cm.Spectral(np.linspace(0, 0.8, y_unique.size)) # plt.cm.Spectral 作用:在画图时为不同类别的样本分别分配不同的颜色
print(clrs)
for k, clr in zip(y_unique, clrs): # zip() 函数:将可迭代的对象作为参数,把对象中对应的元素打包成一个个元组,并返回由这些元组组成的对象
cur = (y_hat == k)
cur = (y_hat == k)
if k == -1:
plt.scatter(data[cur, 0], data[cur, 1], s=20, c='k') # 散点图,用于绘制未分类样本。c='k':黑色
continue
plt.scatter(data[cur, 0], data[cur, 1], s=30, c=clr, edgecolors='k') # 散点图,绘制正常节点
plt.scatter(data[cur & core_indices][:, 0], data[cur & core_indices][:, 1], s=60, c=clr, marker='o',
edgecolors='k') # 绘制边界点
x1_min, x2_min = np.min(data, axis=0) # 分别找到数据的两列中的最小值
x1_max, x2_max = np.max(data, axis=0) # 分别找到数据的两列中的最大值
x1_min, x1_max = expand(x1_min, x1_max)
x2_min, x2_max = expand(x2_min, x2_max)
plt.xlim((x1_min, x1_max)) # 设置 x 轴的数值显示范围
plt.ylim((x2_min, x2_max)) # 设置 y 轴的数值显示范围
plt.grid(True) # 网格
plt.title(u'epsilon = %.1f m = %d,聚类数目:%d' % (eps, min_samples, n_clusters), fontsize=16) # 子图的标题
plt.tight_layout() # 会自动调整子图参数,使之填充整个图像区域(防止重叠)
plt.subplots_adjust(top=0.9)
plt.savefig('cluster_DBSCAN') # 将绘图结果保存为png图片
plt.show() # 展示
结果展示:
从图中可看出,密度聚类存在的一个问题:
- 有些点无法聚到任何簇中,即:离群点(噪声点)
离群点为什么聚不进来?
- 半径够不到、或者 m(最少样本个数)设置的比较大——密度不可达
六、谱聚类(了解即可)
谱聚类的本质:先做降维,再用 K-Means
谱聚类的特点
优点:
- 对数据的结构没有假设(适应性广)
- 经过特殊的构图处理后计算很快
- 不会像 K-Means 一样将一些离散的小簇聚在一起
缺点:
- 对于不同的构图方式比较敏感
- 对于超参数设置比较敏感
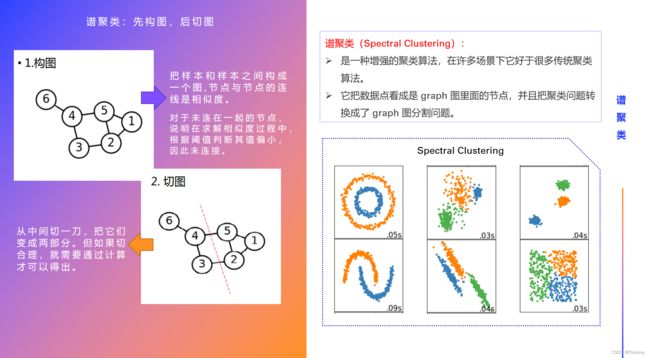
谱聚类整体思路
- 先构图,后切图
1. 构图
一个典型的实现由三个基本步骤组成:
- 根据训练集,计算相似度矩阵 S S S
- 根据相似度矩阵,采用某种构图方法计算 W W W 权重矩阵
- 根据 W W W 权重矩阵,计算 D D D 矩阵和拉普拉斯矩阵
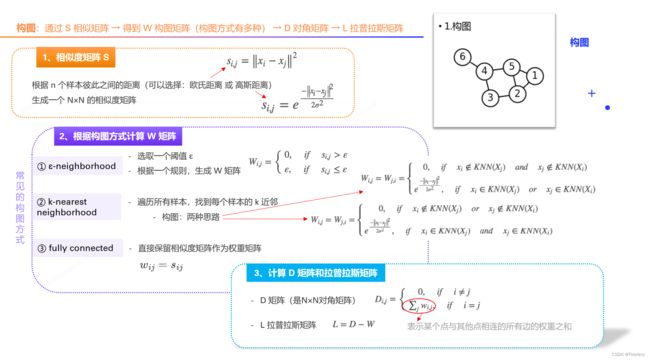
∴ 构图:通过 S S S 相似矩阵 → 得到 W W W 构图矩阵(构图方式有多种) → D D D 对角矩阵 → L L L 拉普拉斯矩阵
步骤一:相似度矩阵 S S S
- 根据 n n n 个样本彼此之间的距离(可以选择:欧氏距离 或 高斯距离)生成一个 N × N N×N N×N 的相似度矩阵
- 欧式距离: s i , j = ∥ x i − x j ∥ 2 s_{i,j}=\left \| x_i -x_j\right \|^{2} si,j=∥xi−xj∥2
- 高斯距离: s i , j = e − ∥ x i − x j ∥ 2 2 σ 2 s_{i,j}=e^{\frac{-\left \| x_i -x_j\right \|^{2}}{2\sigma ^{2}}} si,j=e2σ2−∥xi−xj∥2
- 得到了 S S S 矩阵
- S S S 矩阵:样本与样本间,两两求相似度,把所有数据都填起来的矩阵
步骤二:根据构图方式计算 W W W 矩阵(邻接矩阵)
W W W 矩阵:想表达的是——如何构建的
常见构图方式:
-
① ε-neighborhood( ε ε ε-邻近法)
- 选取一个阈值 ε ε ε
- 根据一个规则,生成 W W W 矩阵
- 每一个点连接到与其 ε ε ε 半径内的所有点;
- 如果在半径内,权重就是 ε ε ε ,否则就是0,没有其他的信息了。
- 说明: 距离远近度量很不精确,因此在实际应用中,我们很少使用
-
② k-nearest neighborhood(K 近邻法)
- 一个参数 k 首先固定下来
- 利用 KNN 算法(K 近邻)遍历所有的样本点,取每个样本最近的 k 个点作为邻近,只有和样本距离最近的 k 个点之间的 w i j > 0 w_{ij}\gt0 wij>0
- 但是这种方法会造成邻接矩阵 W W W 非对称,后面的算法需要对称邻接矩阵。
- 为了解决上述问题,一般采取下面两种方法其一:
- a)K 近邻法是只要一个点在另一个点的 K 近邻中,则保留 s i , j s_{i,j} si,j;
- b)K 近邻法是必须两个点互为 K 近邻,才能保留 s i , j s_{i,j} si,j。
-
③ fully connected(全连接法)
- 直接保留相似度矩阵作为权重矩阵
- 说明:实际应用中,建立邻接矩阵中最普遍的使用全连接法来建立
步骤三:计算 D D D 矩阵和拉普拉斯矩阵
2. 切图
切图的过程,就是聚类的过程
内容:
- 对于原始图的任意两个子图 A 、 B A、B A、B 满足 A ∩ B = ∅ A∩B=∅ A∩B=∅(即:两图无相交部分)
- 定义切图权重为: W ( A , B ) = ∑ w i j , i ∈ A , j ∈ B W(A,B)= \sum w_{ij},i\in A,j\in B W(A,B)=∑wij,i∈A,j∈B
- 衡量最终切图结果:
- 假设原始图 V V V 切为了 k k k 个子图( A 1 , A 2 , . . . , A K A_1,A_2,...,A_K A1,A2,...,AK),有 A 1 ∪ A 2 ∪ . . . ∪ A K = V A_1\cup A_2\cup ...\cup A_K = V A1∪A2∪...∪AK=V 且 A 1 ∩ A 2 ∩ . . . ∩ A K = ∅ A_1\cap A_2\cap ...\cap A_K = ∅ A1∩A2∩...∩AK=∅ ,
- 定义 c u t ( A 1 , A 2 , . . . , A K ) = 1 2 ∑ i k W ( A i , A i ˉ ) cut(A_1,A_2,...,A_K)=\frac{1}{2}\sum_{i}^{k}W(A_i,\bar{A_i}) cut(A1,A2,...,AK)=21∑ikW(Ai,Aiˉ) (其中, A i ˉ \bar{A_i} Aiˉ 为 A i A_i Ai 的补集),为该种切法的切边权重和
切图的目的:
- 每个子图内部:连边的权重平均都较大
- 每个子图之间:尽量没有边相连,或者连边的权重很低
思考:
- 如何切图可以让子图内的点权重之和高,子图间的点权重之和低呢?
- 一个自然的想法就是最小化 c u t ( A 1 , A 2 , … , A k ) cut(A_1,A_2,\ldots,A_k) cut(A1,A2,…,Ak),但是可以发现,这种极小化的切图存在问题
切图的问题:
切图方法 ☞ RatioCut:
- 对于 L L L 矩阵(拉普拉斯矩阵)取最小的 k 1 k_1 k1 个特征值对应的特征向量(每个向量的形状是是 1 ∗ n 1*n 1∗n )
- 说明:求特征值、特征向量:相当于 降维
- 特征向量:相当于方向
- 特征值:方向上的信息量
- 说明:求特征值、特征向量:相当于 降维
- 将 k 1 k_1 k1 个列向量拼成一个 N N N 行 k 1 k_1 k1 列的矩阵 H H H
- 对这个 H H H 矩阵按行做标准化
- 设定超参数 k 2 k_2 k2,对标准化后的 H H H 矩阵进行 K-Means 聚类,得到的结果便是按照 RatioCut 标准划分出来的子集
- 白话:把原来的点,在不同的坐标系上进行相对应的投影,把投影完后的结果,通过 K-means 进行聚类
3. 基于 sklearn 的谱聚类代码
下面是基于 sklearn 库做的聚类,感受不同超参数下的谱聚类效果
代码:( 工具:PyCharm,基于:python3)
# 导入模块
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.colors
from sklearn.cluster import spectral_clustering # 谱聚类
from sklearn.metrics import euclidean_distances # 欧式距离
def expand(a, b):
d = (b - a) * 0.1
return a-d, b+d
if __name__ == "__main__":
# -----创建数据-----
t = np.arange(0, 2*np.pi, 0.1)
data1 = np.vstack((np.cos(t), np.sin(t))).T
data2 = np.vstack((2*np.cos(t), 2*np.sin(t))).T
data3 = np.vstack((3*np.cos(t), 3*np.sin(t))).T
data = np.vstack((data1, data2, data3))
n_clusters = 3
m = euclidean_distances(data, squared=True) # 欧式距离的开根号(矩阵)
sigma = np.median(m) # 中位数
# ------------- 绘图 --------------
matplotlib.rcParams['font.sans-serif'] = [u'SimHei'] # 可展示中文(黑体)
matplotlib.rcParams['axes.unicode_minus'] = False # 让负号可以正常显示
plt.figure(figsize=(12, 8), facecolor='w')
plt.suptitle(u'谱聚类', fontsize=20)
clrs = plt.cm.Spectral(np.linspace(0, 0.8, n_clusters))
for i, s in enumerate(np.logspace(-2, 0, 6)):
print(s)
af = np.exp(-m ** 2 / (s ** 2)) + 1e-6 # 此处 s 用来判断高斯距离;‘+ 1e-6’:是为了防止值为0
y_hat = spectral_clustering(af, n_clusters=n_clusters, assign_labels='kmeans', random_state=1)
plt.subplot(2, 3, i+1)
for k, clr in enumerate(clrs):
cur = (y_hat == k)
plt.scatter(data[cur, 0], data[cur, 1], s=40, c=clr, edgecolors='k')
x1_min, x2_min = np.min(data, axis=0)
x1_max, x2_max = np.max(data, axis=0)
x1_min, x1_max = expand(x1_min, x1_max)
x2_min, x2_max = expand(x2_min, x2_max)
plt.xlim((x1_min, x1_max))
plt.ylim((x2_min, x2_max))
plt.grid(True) # 网格
plt.title(u'sigma = %.2f' % s, fontsize=16) # 子图的标题
plt.tight_layout() # 会自动调整子图参数,使之填充整个图像区域(防止重叠)
plt.subplots_adjust(top=0.9)
plt.savefig('cluster_spectral') # 将绘图结果保存为png图片
plt.show() # 展示
结果展示:
—— 说明:本文写于 2022.9.2 和 9.18~9.28 ,文中内容基于 python3,使用工具 PyCharm 编写的代码