解析NLP竞赛中的提分点-对抗训练
欢迎大家访问个人博客:https://jmxgodlz.xyz
前言
在NLP比赛中,对抗训练是常见的提分手段。本文将详细介绍对抗训练的场景、作用、类型、具体实现以及未来的展望。
对抗训练应用场景
Szegedy在14年的ICLR中提出了对抗样本的概念。对抗样本可以用来攻击和防御,而对抗训练其实是“对抗”家族中防御的一种方式,其基本原理为:通过添加扰动构建对抗样本,喂入模型一同训练,提高模型遇到对抗样本时的鲁棒性,同时一定程度也能提高模型的表现和泛化能力。
对抗样本一般需要具有两个特点:
- 相对于原始输入,所添加的扰动是微小的;
- 能使模型犯错。
对抗训练的公式如下:
min θ E ( x , y ) ∼ D [ max r a d v ∈ S L ( θ , x + r a d v , y ) ] \min _{\theta} \mathbb{E}_{(x, y) \sim \mathcal{D}}\left[\max _{r_{a d v} \in \mathcal{S}} L\left(\theta, x+r_{a d v}, y\right)\right] θminE(x,y)∼D[radv∈SmaxL(θ,x+radv,y)]
该过程可以分为两步:
- 内部的max过程:寻找让模型犯错最大的扰动
- 外部的min过程:寻找整体损失最小的参数
在图像领域,扰动可以为图像上的噪点,但是在NLP中,如果直接在词编码上加上扰动,输入会偏离原先的语义。由于向量空间中语义相近的词语相互接近,在向量空间中添加微小的扰动的方式并不会对语义带来较大的破坏,因此当前NLP中的对抗训练均针对embedding做扰动。
对抗训练的作用
- 提高模型应对恶意对抗样本时的鲁棒性。
- 作为一种正则化方式(regularization),减少过拟合(overfitting),提高泛化能力。
在NLP任务中,对抗训练的角色不再是为了防御基于梯度的恶意攻击,更多的是作为一种正则化方式(regularization),提高模型的泛化能力。
对抗训练具体方式FGM/PGD/FreeLB
API介绍
在介绍对抗训练的具体实现之前,本文先介绍下面Pytorch代码中常见的函数:
一般优化流程:
# zero the parameter gradients
optimizer.zero_grad()
# forward + backward + optimize
outputs = net(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
具体展开流程:
# gradient descent
weights = [0] * n
alpha = 0.0001
max_Iter = 50000
for i in range(max_Iter):
loss = 0
d_weights = [0] * n
for k in range(m):
h = dot(input[k], weights)
d_weights = [d_weights[j] + (label[k] - h) * input[k][j] for j in range(n)] # 梯度下降优化
loss += (label[k] - h) * (label[k] - h) / 2 # 梯度下降优化
d_weights = [d_weights[k]/m for k in range(n)]
weights = [weights[k] + alpha * d_weights[k] for k in range(n)]
if i%10000 == 0:
print "Iteration %d loss: %f"%(i, loss/m)
print weights
可以发现它们实际上是一一对应的:
- optimizer.zero_grad()对应d_weights = [0] * n
该步骤将梯度初始化为零(因为一个batch的loss关于weight的导数是所有sample的loss关于weight的导数的累加和)
- outputs = net(inputs)对应h = dot(input[k], weights)
该步骤即前向传播求出预测的值
- loss = criterion(outputs, labels)对应loss += (label[k] - h) * (label[k] - h) / 2
该步骤为求当前具体loss值
- loss.backward()对应d_weights = [d_weights[j] + (label[k] - h) * input[k][j] for j in range(n)]
该步骤即反向传播求梯度
- optimizer.step()对应weights = [weights[k] + alpha * d_weights[k] for k in range(n)]
该步骤即更新所有参数
FGSM/FGM
该方式的思想为沿着梯度上升方向对扰动可以对模型带来最大的破坏。
FGSM:采用Sign函数对梯度采取max归一化,max归一化是是说如果梯度某个维度上的值为正,则设为1;如果为负,则设为-1;如果为0,则设为0
FGM:采用L2归一化,L2归一化则将梯度的每个维度的值除以梯度的L2范数。 理论上L2归一化更严格的保留了梯度的方向,但是max归一化则不一定和原始梯度的方向相同。
F G S M : δ = ϵ S i g n ( g ) FGSM:\delta=\epsilon Sign(g) FGSM:δ=ϵSign(g)
F G M : δ = ϵ ( g / ∣ ∣ g 2 ∣ ∣ ) FGM: \delta = \epsilon (g/||g_2||) FGM:δ=ϵ(g/∣∣g2∣∣)
其 中 g 为 梯 度 g = ∇ x ( L ( f θ ( X ) , y ) ) 其中g为梯度g=\nabla x(L(f_{\theta}(X), y)) 其中g为梯度g=∇x(L(fθ(X),y))
import torch
class FGM():
def __init__(self, model):
self.model = model
self.backup = {}
def attack(self, epsilon=1., emb_name='emb.'):
# emb_name这个参数要换成你模型中embedding的参数名
for name, param in self.model.named_parameters():
if param.requires_grad and emb_name in name:
self.backup[name] = param.data.clone()
norm = torch.norm(param.grad)
if norm != 0 and not torch.isnan(norm):
r_at = epsilon * param.grad / norm
param.data.add_(r_at)
def restore(self, emb_name='emb.'):
# emb_name这个参数要换成你模型中embedding的参数名
for name, param in self.model.named_parameters():
if param.requires_grad and emb_name in name:
assert name in self.backup
param.data = self.backup[name]
self.backup = {}
# 初始化
fgm = FGM(model)
for batch_input, batch_label in data:
# 正常训练
loss = model(batch_input, batch_label)
loss.backward() # 反向传播,得到正常的grad
# 对抗训练
fgm.attack() # 在embedding上添加对抗扰动
loss_adv = model(batch_input, batch_label)
loss_adv.backward() # 反向传播,并在正常的grad基础上,累加对抗训练的梯度
fgm.restore() # 恢复embedding参数
# 梯度下降,更新参数
optimizer.step()
model.zero_grad()
FGM/FGSM 流程总结
- 正常的前向传播-得到梯度与loss值
- 执行对抗训练-根据当前梯度对参数值添加扰动;前向传播得到损失与最终梯度
- 恢复embedding参数
- 更新本次迭代的参数
根据min-max公式可以看出,对抗训练主要完成内部max的过程。FGM/FGSM思想就是沿着梯度上升的方向,找寻最优解。但是FGM/FGSM 有假设:损失函数是线性或者局部线性。如果不是线性,那梯度提升方向不一定是最优方向。
PGD
为了解决FGM中线性假设问题,PGD分多次迭代,若扰动超出范围将扰动映射到规定范围内。
X t + 1 = ∏ X + S ( X t + ϵ ( g t / ∣ ∣ g t ∣ ∣ ) ) X_{t + 1}=\prod _{X+S}(X_t + \epsilon(g_t/||g_t||)) Xt+1=X+S∏(Xt+ϵ(gt/∣∣gt∣∣))
其 中 g 为 梯 度 g t = ∇ x t ( L ( f θ ( X t ) , y ) ) 其中g为梯度g_t=\nabla x_t(L(f_{\theta}(X_t), y)) 其中g为梯度gt=∇xt(L(fθ(Xt),y))
虽然PGD很有效,但效率并不高,若经过m次迭代,PGD需要迭代m*(K + 1)次。其代码展示如下:
import torch
class PGD():
def __init__(self, model):
self.model = model
self.emb_backup = {}
self.grad_backup = {}
def attack(self, epsilon=1., alpha=0.3, emb_name='emb.', is_first_attack=False):
# emb_name这个参数要换成你模型中embedding的参数名
for name, param in self.model.named_parameters():
if param.requires_grad and emb_name in name:
if is_first_attack:
self.emb_backup[name] = param.data.clone()
norm = torch.norm(param.grad)
if norm != 0 and not torch.isnan(norm):
r_at = alpha * param.grad / norm
param.data.add_(r_at)
param.data = self.project(name, param.data, epsilon)
def restore(self, emb_name='emb.'):
# emb_name这个参数要换成你模型中embedding的参数名
for name, param in self.model.named_parameters():
if param.requires_grad and emb_name in name:
assert name in self.emb_backup
param.data = self.emb_backup[name]
self.emb_backup = {}
def project(self, param_name, param_data, epsilon):
r = param_data - self.emb_backup[param_name]
if torch.norm(r) > epsilon:
r = epsilon * r / torch.norm(r)
return self.emb_backup[param_name] + r
def backup_grad(self):
for name, param in self.model.named_parameters():
if param.requires_grad:
self.grad_backup[name] = param.grad.clone()
def restore_grad(self):
for name, param in self.model.named_parameters():
if param.requires_grad:
param.grad = self.grad_backup[name]
pgd = PGD(model)
K = 3
for batch_input, batch_label in data:
# 正常训练
loss = model(batch_input, batch_label)
loss.backward() # 反向传播,得到正常的grad
pgd.backup_grad()
# 对抗训练
for t in range(K):
pgd.attack(is_first_attack=(t==0)) # 在embedding上添加对抗扰动, first attack时备份param.data
if t != K-1:
model.zero_grad()
else:
pgd.restore_grad()
loss_adv = model(batch_input, batch_label)
loss_adv.backward() # 反向传播,并在正常的grad基础上,累加对抗训练的梯度
pgd.restore() # 恢复embedding参数
# 梯度下降,更新参数
optimizer.step()
model.zero_grad()
PGD流程总结
- 正常的前向传播-得到梯度与loss值
- 备份正常的梯度
- 执行K次对抗训练
- 若t=0,备份参数;梯度清零;前向传播,计算梯度与loss值
- 若t=K-1;恢复第1步的梯度;前向传播,计算梯度与loss值
- 恢复3.1中的embedding参数
- 更新本次迭代的参数
PGD执行K次目的为分多步获取内部max的扰动-扰动表现在参数上,每一步梯度归零,但是参数值得到了累加: x ′ = x + ∑ t = 0 K r t x^{'}=x+\sum_{t=0}^{K} r_t x′=x+∑t=0Krt,最后根据参数 x ′ x^{'} x′以及初始梯度前向传播计算loss和最终梯度,最后,恢复初始参数,根据最终梯度完成参数更新。
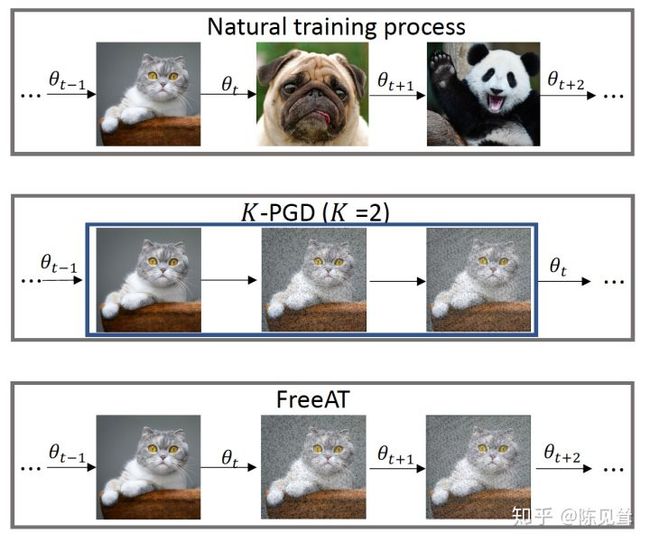
FreeAT
PGD中进行m次反向传播,m *(K + 1) 次前向传播效率不高
FreeAT把前向传播计算出的梯度也进行回传
对比图为:
进行(m/k)*k=m 次反向传播,(m/k)* k = m次前向传播
初始化r=0
对于epoch=1...N/m:
对于每个x:
对于每步m:
1.利用上一步的r,计算x+r的前后向,得到梯度
2.根据梯度更新参数
3.根据梯度更新r
FreeAT流程总结
- 正常的前向传播-得到梯度与loss值
- 备份正常的梯度
- 执行K次对抗训练
- 前向传播得到梯度与loss值
- 根据梯度更新参数
- 根据梯度更新扰动
缺点:FreeLB指出,FreeAT的问题在于每次的r对于当前的参数都是次优的(无法最大化loss),因为当前r是由$ r_{t-1} 和 和 和\theta_{t-1} 计 算 出 来 的 , 是 对 于 计算出来的,是对于 计算出来的,是对于\theta_{ t-1 }$的最优。
FreeLB
FreeLB认为,FreeAT和YOPO对于获得最优r (inner max)的计算都存在问题,因此提出了一种类似PGD的方法。只不过PGD只使用了最后一步x+r输出的梯度,而FreeLB取了每次迭代r输出梯度的平均值,相当于把输入看作一个K倍大的虚拟batch,由[X+r1, X+r2, …, X+rk]拼接而成。具体的公式为:
m i n θ E ( Z , y ) − D ( 1 K ∑ t = 0 K − 1 m a x r t ∈ L t L ( f θ ( X + r t ) , y ) ) min_{\theta} E(Z,y) - D(\frac{1}{K} \sum_{t=0}^{K-1}max_{r_t \in L_t} L(f_{\theta}(X+r_t),y)) minθE(Z,y)−D(K1t=0∑K−1maxrt∈LtL(fθ(X+rt),y))
PGD公式为:
m i n θ E ( Z , y ) − D ( m a x ∣ ∣ r ∣ ∣ ≤ ϵ L ( f θ ( X + r t ) , y ) ) min_{\theta} E(Z,y) - D(max_{||r|| \le\epsilon} L(f_{\theta}(X+r_t),y)) minθE(Z,y)−D(max∣∣r∣∣≤ϵL(fθ(X+rt),y))
FreeLB与PGD区别如下:
- PGD是迭代K次r后取最后一次扰动的梯度更新参数,FreeLB是取K次迭代中的平均梯度
- PGD的扰动范围都在epsilon内,因为流程第3步将梯度归0了,每次投影都会回到以第1步x为圆心,半径是epsilon的圆内,而FreeLB每次的x都会迭代,所以r的范围更加灵活,更可能接近局部最优
伪代码为:
对于每个x:
1.通过均匀分布初始化r,梯度g为0
对于每步t=1...K:
2.根据x+r计算前后向,累计梯度g
3.更新r
4.根据g/K更新梯度
class FreeLB(object):
def __init__(self, adv_K, adv_lr, adv_init_mag, adv_max_norm=0., adv_norm_type='l2', base_model='bert'):
self.adv_K = adv_K
self.adv_lr = adv_lr
self.adv_max_norm = adv_max_norm
self.adv_init_mag = adv_init_mag # adv-training initialize with what magnitude, 即我们用多大的数值初始化delta
self.adv_norm_type = adv_norm_type
self.base_model = base_model
def attack(self, model, inputs, gradient_accumulation_steps=1):
input_ids = inputs['input_ids']
if isinstance(model, torch.nn.DataParallel):
embeds_init = getattr(model.module, self.base_model).embeddings.word_embeddings(input_ids)
else:
embeds_init = getattr(model, self.base_model).embeddings.word_embeddings(input_ids)
if self.adv_init_mag > 0: # 影响attack首步是基于原始梯度(delta=0),还是对抗梯度(delta!=0)
input_mask = inputs['attention_mask'].to(embeds_init)
input_lengths = torch.sum(input_mask, 1)
if self.adv_norm_type == "l2":
delta = torch.zeros_like(embeds_init).uniform_(-1, 1) * input_mask.unsqueeze(2)
dims = input_lengths * embeds_init.size(-1)
mag = self.adv_init_mag / torch.sqrt(dims)
delta = (delta * mag.view(-1, 1, 1)).detach()
elif self.adv_norm_type == "linf":
delta = torch.zeros_like(embeds_init).uniform_(-self.adv_init_mag, self.adv_init_mag)
delta = delta * input_mask.unsqueeze(2)
else:
delta = torch.zeros_like(embeds_init) # 扰动初始化
loss, logits = None, None
for astep in range(self.adv_K):
delta.requires_grad_()
inputs['inputs_embeds'] = delta + embeds_init # 累积一次扰动delta
inputs['input_ids'] = None
outputs = model(**inputs)
loss, logits = outputs[:2] # model outputs are always tuple in transformers (see doc)
loss = loss.mean() # mean() to average on multi-gpu parallel training
loss = loss / gradient_accumulation_steps
loss.backward()
delta_grad = delta.grad.clone().detach() # 备份扰动的grad
if self.adv_norm_type == "l2":
denorm = torch.norm(delta_grad.view(delta_grad.size(0), -1), dim=1).view(-1, 1, 1)
denorm = torch.clamp(denorm, min=1e-8)
delta = (delta + self.adv_lr * delta_grad / denorm).detach()
if self.adv_max_norm > 0:
delta_norm = torch.norm(delta.view(delta.size(0), -1).float(), p=2, dim=1).detach()
exceed_mask = (delta_norm > self.adv_max_norm).to(embeds_init)
reweights = (self.adv_max_norm / delta_norm * exceed_mask + (1 - exceed_mask)).view(-1, 1, 1)
delta = (delta * reweights).detach()
elif self.adv_norm_type == "linf":
denorm = torch.norm(delta_grad.view(delta_grad.size(0), -1), dim=1, p=float("inf")).view(-1, 1, 1) # p='inf',无穷范数,获取绝对值最大者
denorm = torch.clamp(denorm, min=1e-8) # 类似np.clip,将数值夹逼到(min, max)之间
delta = (delta + self.adv_lr * delta_grad / denorm).detach() # 计算该步的delta,然后累加到原delta值上(梯度上升)
if self.adv_max_norm > 0:
delta = torch.clamp(delta, -self.adv_max_norm, self.adv_max_norm).detach()
else:
raise ValueError("Norm type {} not specified.".format(self.adv_norm_type))
if isinstance(model, torch.nn.DataParallel):
embeds_init = getattr(model.module, self.base_model).embeddings.word_embeddings(input_ids)
else:
embeds_init = getattr(model, self.base_model).embeddings.word_embeddings(input_ids)
return loss, logits
if args.do_adv:
inputs = {
"input_ids": input_ids,
"bbox": layout,
"token_type_ids": segment_ids,
"attention_mask": input_mask,
"masked_lm_labels": lm_label_ids
}
loss, prediction_scores = freelb.attack(model, inputs)
loss.backward()
optimizer.step()
scheduler.step()
model.zero_grad()
class FreeLB():
def __init__(self, model, args, optimizer, base_model='xlm-roberta'):
self.args = args
self.model = model
self.adv_K = self.args.adv_K
self.adv_lr = self.args.adv_lr
self.adv_max_norm = self.args.adv_max_norm
self.adv_init_mag = self.args.adv_init_mag # adv-training initialize with what magnitude, 即我们用多大的数值初始化delta
self.adv_norm_type = self.args.adv_norm_type
self.base_model = base_model
self.optimizer = optimizer
def attack(self, model, inputs):
args = self.args
input_ids = inputs['input_ids']
#获取初始化时的embedding
embeds_init = getattr(model, self.base_model).embeddings.word_embeddings(input_ids.to(args.device))
if self.adv_init_mag > 0: # 影响attack首步是基于原始梯度(delta=0),还是对抗梯度(delta!=0)
input_mask = inputs['attention_mask'].to(embeds_init)
input_lengths = torch.sum(input_mask, 1)
if self.adv_norm_type == "l2":
delta = torch.zeros_like(embeds_init).uniform_(-1, 1) * input_mask.unsqueeze(2)
dims = input_lengths * embeds_init.size(-1)
mag = self.adv_init_mag / torch.sqrt(dims)
delta = (delta * mag.view(-1, 1, 1)).detach()
else:
delta = torch.zeros_like(embeds_init) # 扰动初始化
# loss, logits = None, None
for astep in range(self.adv_K):
delta.requires_grad_()
inputs['inputs_embeds'] = delta + embeds_init # 累积一次扰动delta
# inputs['input_ids'] = None
loss, _ = model(input_ids=None,
attention_mask=inputs["attention_mask"].to(args.device),
token_type_ids=inputs["token_type_ids"].to(args.device),
labels=inputs["sl_labels"].to(args.device),
inputs_embeds=inputs["inputs_embeds"].to(args.device))
loss = loss / self.adv_K # 求平均的梯度
loss.backward()
if astep == self.adv_K - 1:
# further updates on delta
break
delta_grad = delta.grad.clone().detach() # 备份扰动的grad
if self.adv_norm_type == "l2":
denorm = torch.norm(delta_grad.view(delta_grad.size(0), -1), dim=1).view(-1, 1, 1)
denorm = torch.clamp(denorm, min=1e-8)
delta = (delta + self.adv_lr * delta_grad / denorm).detach()
if self.adv_max_norm > 0:
delta_norm = torch.norm(delta.view(delta.size(0), -1).float(), p=2, dim=1).detach()
exceed_mask = (delta_norm > self.adv_max_norm).to(embeds_init)
reweights = (self.adv_max_norm / delta_norm * exceed_mask + (1 - exceed_mask)).view(-1, 1, 1)
delta = (delta * reweights).detach()
else:
raise ValueError("Norm type {} not specified.".format(self.adv_norm_type))
embeds_init = getattr(model, self.base_model).embeddings.word_embeddings(input_ids.to(args.device))
return loss
for batch_input, batch_label in data:
# 正常训练
loss = model(batch_input, batch_label)
loss.backward() # 反向传播,得到正常的grad
# 对抗训练
freelb = FreeLB( model, args, optimizer, base_model)
loss_adv = freelb.attack(model, batch_input)
loss_adv.backward() # 反向传播,并在正常的grad基础上,累加对抗训练的梯度
# 梯度下降,更新参数
optimizer.step()
model.zero_grad()
FreeLB流程总结
- 正常的前向传播-得到梯度与loss值
- 备份正常的梯度
- 执行K次对抗训练
- 前向传播,计算梯度与loss值
- 梯度累加
- 根据梯度计算扰动
- 恢复初始embedding参数
- 更新本次迭代的参数
该方法与FreeAT一样都想高效的利用两种梯度。不同的是,该方法并不是每次都进行更新,而是将参数梯度累积起来,用累积的梯度对参数更新。
通用范式
通过对上述几种对抗训练方式的学习,不难看出对抗训练的目的为完成内部max的任务,找出最大扰动的最优解。具体表现为:求解最大扰动更新参数;根据参数进行前向传播得到loss与最终梯度;恢复最初的参数值;利用最终的梯度对最初的参数值进行更新。所以通用流程表示如下:
1. 正常的前向传播-得到梯度与loss值
2. 备份正常的参数
3. 求解扰动最优值,更新参数
4. 根据更新后参数以及最初梯度,前向传播得到最终梯度
5. 恢复最初的参数
6. 根据最初的参数与最终梯度,完成参数的更新
不同对抗训练方式体现为求解扰动最优值的方式不同:
- FGM/FGSM最优值求解方式为:一步到位,根据最初的梯度与参数值,得到扰动值
- PGD最优值求解方式为:多步走,每一步根据上一步的参数获取扰动并更新参数,最终得到多步累加的扰动值
- FreeAT最优值求解方式为:与PGD一样分多步,但是该方法相当于:每一步根据上一步参数和梯度获取的扰动值就是最终扰动值
- FreeLB最优值求解方式为:与PGD一样分多步,但是在最后进行梯度更新的时候,最终梯度为初始梯度加上每一步梯度的平均值
对抗训练展望
虚拟对抗训练
那什么是虚拟对抗训练(VAT)呢?
VAT不需要标签信息,可应用于无监督学习,其梯度上升的方向是能使预测的输出分布偏离现状的方向,而传统对抗训练课找的是使模型预测最大地偏离label的方向。因此,VAT不使用真实label,而是“虚拟”label——当前模型的预测结果。
该部分可以查看JayJay的博客:虚拟对抗训练:让预训练模型再次强大!
延伸思考
对抗训练与梯度惩罚
该内容为苏神在博客对抗训练浅谈:意义、方法和思考(附Keras实现)中所提及:
假设已经得到对抗扰动Δx,那么我们在更新θ时,考虑对 L ( x + Δ x , y ; θ ) L(x+Δx,y;θ) L(x+Δx,y;θ)的展开:
min θ E ( x , y ) ∼ D [ L ( x + Δ x , y ; θ ) ] ≈ min θ E ( x , y ) ∼ D [ L ( x , y ; θ ) + ⟨ ∇ x L ( x , y ; θ ) , Δ x ⟩ ] \min_{\theta}\mathbb{E}_{(x,y)\sim\mathcal{D}}\left[L(x+\Delta x, y;\theta)\right]\\ \approx\, \min_{\theta}\mathbb{E}_{(x,y)\sim\mathcal{D}}\left[L(x, y;\theta)+\langle\nabla_x L(x, y;\theta), \Delta x\rangle\right] θminE(x,y)∼D[L(x+Δx,y;θ)]≈θminE(x,y)∼D[L(x,y;θ)+⟨∇xL(x,y;θ),Δx⟩]
对应的θ的梯度为:
∇ θ L ( x , y ; θ ) + ⟨ ∇ θ ∇ x L ( x , y ; θ ) , Δ x ⟩ \nabla_{\theta}L(x, y;\theta)+\langle\nabla_{\theta}\nabla_x L(x, y;\theta), \Delta x\rangle ∇θL(x,y;θ)+⟨∇θ∇xL(x,y;θ),Δx⟩
代入 Δ x = ϵ ∇ x L ( x , y ; θ ) \Delta x=\epsilon \nabla_x L(x, y;\theta) Δx=ϵ∇xL(x,y;θ),得到
∇ θ L ( x , y ; θ ) + ϵ ⟨ ∇ θ ∇ x L ( x , y ; θ ) , ∇ x L ( x , y ; θ ) ⟩ = ∇ θ ( L ( x , y ; θ ) + 1 2 ϵ ∥ ∇ x L ( x , y ; θ ) ∥ 2 ) \nabla_{\theta}L(x, y;\theta)+\epsilon\langle\nabla_{\theta}\nabla_x L(x, y;\theta), \nabla_x L(x, y;\theta)\rangle\\ =\,\nabla_{\theta}\left(L(x, y;\theta)+\frac{1}{2}\epsilon\left\Vert\nabla_x L(x, y;\theta)\right\Vert^2\right) ∇θL(x,y;θ)+ϵ⟨∇θ∇xL(x,y;θ),∇xL(x,y;θ)⟩=∇θ(L(x,y;θ)+21ϵ∥∇xL(x,y;θ)∥2)
这个结果表示,对输入样本施加 ϵ ∇ x L ( x , y ; θ ) \epsilon \nabla_x L(x, y;\theta) ϵ∇xL(x,y;θ)的对抗扰动,一定程度上等价于往loss里边加入“梯度惩罚”
1 2 ϵ ∥ ∇ x L ( x , y ; θ ) ∥ 2 \frac{1}{2}\epsilon\left\Vert\nabla_x L(x, y;\theta)\right\Vert^2 21ϵ∥∇xL(x,y;θ)∥2
如果对抗扰动是 ∇ x L ( x , y ; θ ) / ∥ ∇ x L ( x , y ; θ ) ∥ \nabla_x L(x, y;\theta)/\Vert \nabla_x L(x, y;\theta)\Vert ∇xL(x,y;θ)/∥∇xL(x,y;θ)∥,那么对应的梯度惩罚项则是 ϵ ∥ ∇ x L ( x , y ; θ ) ∥ \epsilon\left\Vert\nabla_x L(x, y;\theta)\right\Vert ϵ∥∇xL(x,y;θ)∥(少了个1/2,也少了个2次方)。
事实上,这个结果不是新的,它首先出现论文《Improving the Adversarial Robustness and Interpretability of Deep Neural Networks by Regularizing their Input Gradients》里。只不过这篇文章不容易搜到,因为你一旦搜索“adversarial training gradient penalty”等关键词,出来的结果几乎都是WGAN-GP相关的东西。
词向量空间
NLP中对抗训练目前的方式均是对embedding向量空间添加扰动,那么向量空间究竟什么样呢?在对比学习的研究中,同样提出一个好的对比学习系统应该具体两个特点:
- **Alignment:**指的是相似的例子,也就是正例,映射到单位超球面后,应该有接近的特征,也即是说,在超球面上距离比较近
- **Uniformity:**指的是系统应该倾向在特征里保留尽可能多的信息,这等价于使得映射到单位超球面的特征,尽可能均匀地分布在球面上,分布得越均匀,意味着保留的信息越充分。分布均匀意味着两两有差异,也意味着各自保有独有信息,这代表信息保留充分。
极端情况下会出现模型塌缩的情况,即所有特征映射到同一点:
笔者认为,对抗训练在词向量层添加扰动,与对比学习类似,实现相似的例子在向量空间中相接近的目的,完成输入发生微小改变,输出改变幅度也不大的任务。