基于倒谱法、自相关法、短时幅度差法的基音频率估计算法（MATLAB及验证）

基音频率检测

一、概念

何为基音周期？人在发音时，根据声带是否振动可以将语音信号分为清音和浊音两种。浊音携带大量的能量，因此又被称为有声语音，其在时域上有明显的周期性。而清音类似于白噪声，没有明显的周期性。发浊音时，气流通过声门使声带产生张弛震荡式振动，产生准周期的激励脉冲串。这种声带振动的频率称为基音频率；相应的周期就称为基音周期。

基音频率与个人声带的情况有关，包括声带长短、薄厚、韧性、劲度和发音习惯，总的来说基音频率就是说话人的特征之一。而且基音频率还随着人的性别、年龄不同而有所不同。男性大概在70-200Hz，女性大概在200-450Hz之间。

二、检测方法

尽管基音周期在目前有非常多的方法，但这些方法都具有局限性，没有一种检测方法能够适用于不同的说话人、不同的要求环境，主要原因归纳为如下方面：

• 语音信号变化复杂，声门激励的波形并不是完全的周期脉冲串，语音的尾部也不具有声带振动的周期性，对有些清浊音的过渡帧很难判定其的周期性。
• 声道共振峰有时会影响激励信号的谐波结构。
• 在浊音语音段很难对每个基音周期的开始和结束位置进行精确的判断
• 语音信号常常混有噪声
• 基音频率变化范围大，从低音男声的70Hz到儿童女性的450Hz，接近3个倍频程给基音检测带来了一定的困难。

目前基音检测算法大致可以分为两大类：非基于事件检测方法和基于事件检测方法，事件指的是声门闭合。

非基于事件的检测方法主要有：自相关函数法、平均幅度差函数法、倒谱法等。非基于事件的检测方法是利用语音信号短时平稳性这一特点，先将语音信号分为长度一定的语音帧，然后对每一帧语音求基音周期。它的优点是：算法简单，运算量小，但缺点在于：无法检测帧内基音周期的非平稳变化，检测精度不高。

基于事件的检测方法主要有：小波变换、Hilbert-Huang变换。基于事件的检测方法是通过声门闭合时刻来对基音周期进行估计，而不需要对语音信号进行短时平稳假设。优点是：在时域和频域上有良好的局部特性，能跟踪基音周期的变化，并能将微小的基音周期变化检测出来，检测精度高。缺点是：计算量较大

三、估计一帧信号的基音频率

倒谱法

由于语音$x(i)$是由声门脉冲激励$u(i)$经声道响应$v(i)$滤波而得，即
$$x(i)=u(i)\ast u(i)$$
设这三个量的倒谱分别为$x(i)、u(i)、v(i)$,则有：
$$x(i)=u(i)\ast v(i)$$
由于在倒谱域中$u(i)和v(i)$是相对分离的，说明包含有基音信息的声脉冲倒谱可以与声道响应倒谱分离，因此从倒谱域分离$u(i)和u(i)$。在计算出倒谱后，就在倒谱频率为$P_{min}\sim P_{max}$之间寻找倒谱函数的最大值，倒谱函数最大值对应的样本的点数就是当前帧语音信号的基音周期$T_0(n)$，基音频率为$F_0(N)=f_s/T_0(n)$

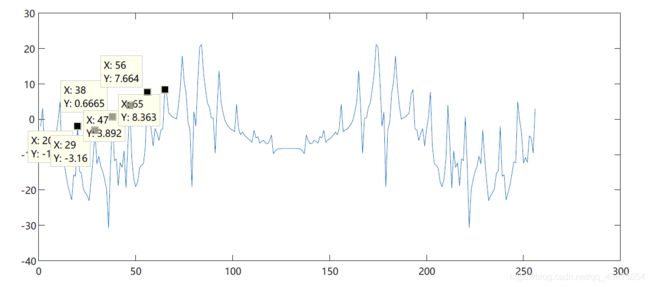
从matlab中取出一帧信号，进行256点的fft变换，再对其求模并取对数后得到幅度谱，取两个相邻的峰值点，如下图所示

clc; close all; clear all;
[x1,Fs] = audioread('voice/a9.wav');
wlen=256; inc=128;          % 给出帧长和帧移
N=length(x1);                    % 信号长度
time=(0:N-1)/Fs;                % 计算出信号的时间刻度
signal=enframe(x1,wlen,inc)';     % 分帧
framedata = signal(:,15);
x2 = fft(framedata);
amp = 20*log10(abs(x2)+0.0000001);
plot(amp)

从图中可以看出两个峰值点的周期相差9，根据FFT的性质，相邻点频率间隔是：
$$\delta =\frac{f_s}{N}=\frac{8000}{256}=31.25Hz$$
因此相差9点周期对应的基频就是：
$$f_b=9\delta =281.25Hz$$
由于FFT变换后两边是对称的，因此用matlab中fftshift（）将对称一边的频谱搬移过来，再取点进行计算，不难发现对应的基频也在281.25Hz。

signal=enframe(x1,wlen,inc)';     % 分帧
framedata = signal(:,15);
x2 = fft(framedata);
amp = 20*log10(abs(x2)+0.0000001);
plot(fftshift(amp));

如果用多个间隔来估计相邻点频率检测，那就是
$$f_b=\frac{65-20}{5}\delta =281.25Hz$$
如果将这个幅度谱看做是时域信号，则其中周期性对应时间周期是：
$$t=9\frac{1}{f_s}=0.001125s$$
所对应的频率就是：
$$f=\frac{f_s}{9}\approx 888.9Hz$$
对幅度谱进行fft变换，获得的新的频域幅度上对应888.9Hz的点数就是
$$\frac{888.9}{\delta }=\frac{888.9}{31.25}=28.4448\approx 28点$$

framedata = signal(:,15);
x2 = fft(framedata);
amp = 20*log10(abs(x2)+0.0000001);
% plot(fftshift(amp));
x3 = fft(fftshift(amp));
amp2 = abs(x3);
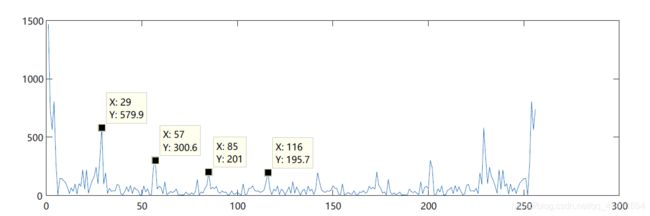
plot(amp2);

从上图中不难看出，他们之间在29~116之间均有峰值，并且间隔大约在28。

过程推导：
$$\begin{gathered} \frac{f_s}{m}\cdot \frac{f_s}{N}=\frac{N}{m}=\frac{888.9}{31.25}=28点 \\ {f}_b=m\frac{f_s}{N}=281.25Hz \end{gathered}$$

所以
$$f_b=\frac{f_s}{28.4448}=281.25Hz$$
想法：

要求一帧信号中的基频，假设如下几个方法：

• 求一帧信号对数幅度谱的FFT谱，取一半之后，找几个峰值点的位置，求出峰值点的间隔

其他软件验证

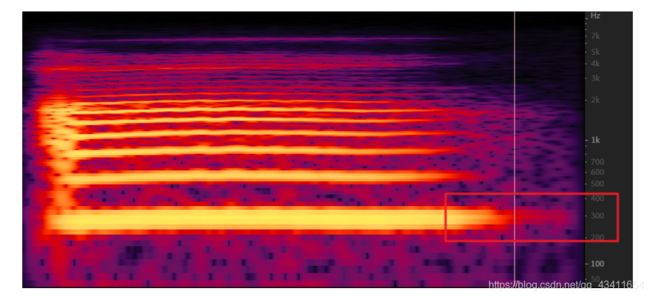
将这个语音放进Adobe audition中，从语谱图来看，第一根能量柱大约是在300Hz往下一点点。

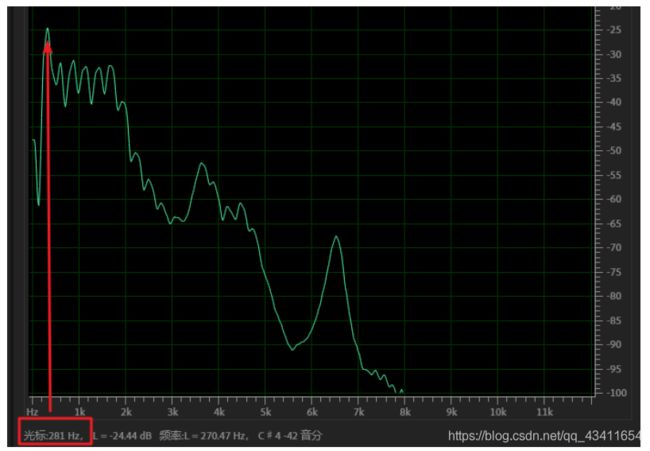
从频谱图来看，第一个峰值所对应的频率是281Hz，与上面求出来的数值误差不大

算法实现

根据上面的想法，自己编写了一个程序来计算基频，大致思路就是多个间隔来估计相邻点频率检测，取两次FFT变换的幅度谱区间的一半，找出这个区间内的极大值点，根据点的个数算出基音频率。

clc; close all; clear all;
[x1,Fs] = audioread('voice/a9.wav');
wlen=256; inc=128;          % 给出帧长和帧移
N=length(x1);                    % 信号长度
time=(0:N-1)/Fs;                % 计算出信号的时间刻度
signal=enframe(x1,wlen,inc)';     % 分帧
framedata = signal(:,15);
x2 = fft(framedata);
amp = 20*log10(abs(x2));
x3 = abs(fft(amp));
x4 = x3(1:128);
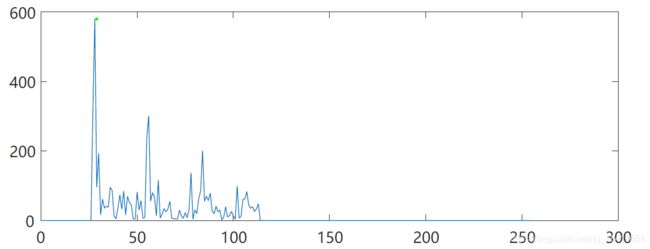
%找出极大值点
datacursormode on
[y,x] = findpeaks(x4,'MinPeakHeight',194);
plot(x4);
% axis([0,128,0,600]);
text(x+.02,y,num2str((1:numel(y))'))
hold on;
plot(x,y,'g.');

%计算fs
x_len = length(x);
x_min = min(x);
x_max = max(x);
fs = (x_max - x_min)/(x_len - 1)*31.25

运行结果如下图所示，算出的基频是437.5Hz，与Au中找出的181Hz有较大差距，从找出极大值的点来看，显然还是点没找对，比如1点，3点应该是排除的，但由于这些点并不是均匀从大到小的，如果将阈值设置的比1还高，那么4,5,6三个点就会被过滤，因此采取设置阈值来寻找极大值的方法不是十分合适的。

最后根据老师的思路，用话音的基音频率的范围来确定x轴范围中的最大值

clc; close all; clear all;
[x1,Fs] = audioread('voice/a9.wav');
wlen=256; inc=128;          % 给出帧长和帧移
N=length(x1);                    % 信号长度
time=(0:N-1)/Fs;                % 计算出信号的时间刻度
signal=enframe(x1,wlen,inc)';     % 分帧
framedata = signal(:,15);
x2 = fft(framedata);
amp = 20*log10(abs(x2));
x3 = abs(fft(amp));
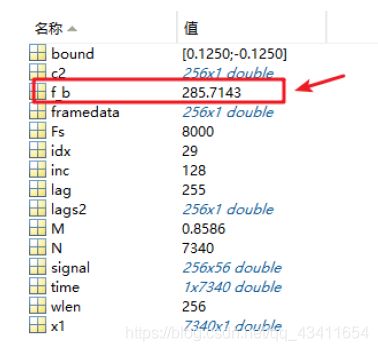
x3(1:27) = 0;%在话音基频范围外的都取零
x3(115:256) = 0;
[M,idx] = max(x3);
f_b=Fs/(idx-1);
plot([0:255],x3);
hold on;
plot(idx,M,'g.');

所求出的基音频率是285.7Hz，与我们刚开始人工求出的281.25Hz还是十分接近的。

短时自相关法

短时自相关法基音检测主要是利用短时自相关函数的性质，通过比较原始信号及其延迟后信号间的类似性来确定基音周期。归一化自相关函数的最大幅值是其他延迟量时，幅值都小于1.如果延迟量等于基音周期，那两个信号具有最大类似性，直接找出短时自相关函数的两个最大值间的距离，就可以作为基音周期的初估值。再求出短时自相关后和倒谱法寻找最大值一样，用相关函数法时也在$P_{min}\sim P_{max}$见寻找归一化相关函数的最大值，最大值对应的延迟量就是基音周期。

还是用原来的元音a的音频，取出一帧来进行短时自相关计算

clc; close all; clear all;
[x1,Fs] = audioread('voice/a9.wav');
%plot(x1);
lag=255;
%观察一段范围的元音
wlen=256; inc=128;          % 给出帧长和帧移
N=length(x1);                    % 信号长度
time=(0:N-1)/Fs;                % 计算出信号的时间刻度
signal=enframe(x1,wlen,inc)';     % 分帧
%取出一帧数据
% frametime = (frame-1)*inc+1:(frame-1)*inc+wlen;
framedata = signal(:,15);
% plot(frametime,framedata);
%对数据进行短时自相关计算
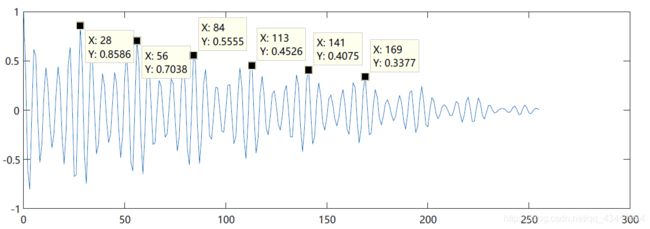
[c2,lags2,bound]=autocorr(framedata,lag);
plot(lags2,c2);

人工计算

取x轴为12,56,113,141的四个点进行计算
$$\begin{gathered} f_{b1}=\frac{8000}{56-28}=285.71Hz \\ {f}_{b2}=\frac{8000}{141-113}=285.71Hz \end{gathered}$$
机器计算

与倒谱法中用到的利用话音的基音频率的范围来确定x轴范围中的最大值来计算基音频率

clc; close all; clear all;
[x1,Fs] = audioread('voice/a9.wav');
%plot(x1);
lag=255;
%观察一段范围的元音
wlen=256; inc=128;          % 给出帧长和帧移
N=length(x1);                    % 信号长度
time=(0:N-1)/Fs;                % 计算出信号的时间刻度
signal=enframe(x1,wlen,inc)';     % 分帧
%取出一帧数据
% frametime = (frame-1)*inc+1:(frame-1)*inc+wlen;
framedata = signal(:,15);
% plot(frametime,framedata);
%对数据进行短时自相关计算
[c2,lags2,bound]=autocorr(framedata,lag);
% plot(lags2,c2);
%在话音基频范围外的都取零
c2(1:27) = 0;
c2(115:256) = 0;
[M,idx] = max(c2);
f_b=Fs/(idx-1);
plot([0:255],c2);
hold on;
plot(idx,M,'g.');

算出的基频是285.7Hz，与手工算出的基频是一致的

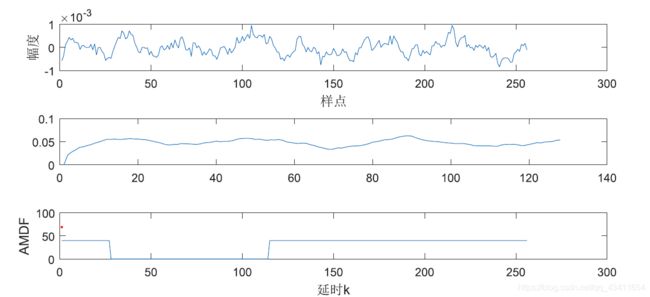
短时幅度差

短时平均幅度差函数：
$$F_n(k)=\sum _{m=0}^{N-1-k}\left|x_n(m)-x_n(m+k)\right|,0<k\le K$$

clc; close all; clear all;
[b,Fs] = audioread('voice/a9.wav');
b1=b(3000:3256); % 选取一段语音
N=128; % 窗口大小
A=[];
for k=1:128; % 延迟长度
    sum=0;
    for m=1:N;
        sum=sum+abs(b1(m)-b1(m+k-1));
    end
    A(k)=sum;
end
% A(1:27) = 100;%在话音基频范围外的都取零
% A(115:256) = 100;
% [M,idx] = min(A);
% f_b=Fs/(idx-1);
% s=b(1:320)
figure(1)
subplot(2,1,1)
plot(b1);
xlabel('样点')
ylabel('幅度')
% axis([0,320,-0.2,0.2])
subplot(2,1,2)
plot(A);
xlabel('延时k')
ylabel('AMDF')
% axis([0,320,0,60]);

计算x=57和x=29两点间的基音频率
$$f_b=\frac{8000}{57-29}=285.71Hz$$

四、估计一段语音的基音频率

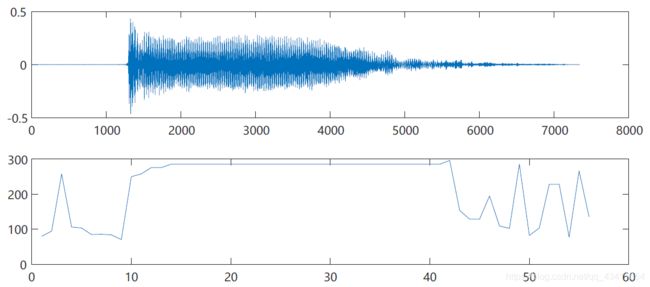
将分帧之后的每一帧数据都进行基频估计，得到该语言每一帧的基音频率图。

倒谱法

%求出一段语音的基音频率
clc; close all; clear all;
[x1,Fs] = audioread('voice/a9.wav');
subplot(2,1,1);
plot(x1);
wlen=256; inc=128;          % 给出帧长和帧移
N=length(x1);                    % 信号长度
time=(0:N-1)/Fs;                % 计算出信号的时间刻度
signal=enframe(x1,wlen,inc)';     % 分帧
[n,m]=size(signal);
for i=1:m
    framedata = signal(:,i);
%     f_b=pitch_cep(framedata,Fs); %倒谱法
%     f_b=pitch_cor(framedata,Fs); %自相关法
    f_b=pitch_admf(framedata,Fs); %平均幅度差
    x(i)=f_b;
end
subplot(2,1,2);
plot(x);

自相关法

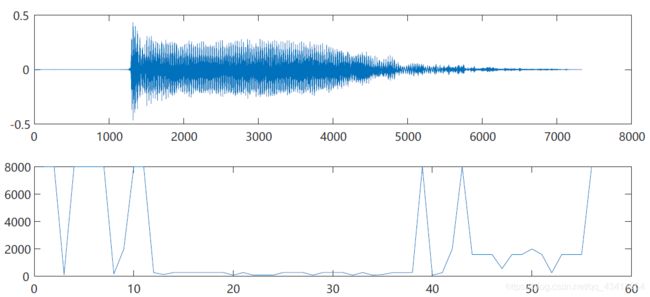
短时幅度差法

画出的出现了基频为8000的时候，究其原因是找两个最小值的点重合了

查看第一帧的图，由于除法公式可以知道，当分母趋于0的时候，结果就会接近最大值

五、利用voicebox验证

还没有办法做到将基频叠加到语谱图中，初步猜想可能需要插值