【文本匹配】之 经典ESIM论文详读
ESIM
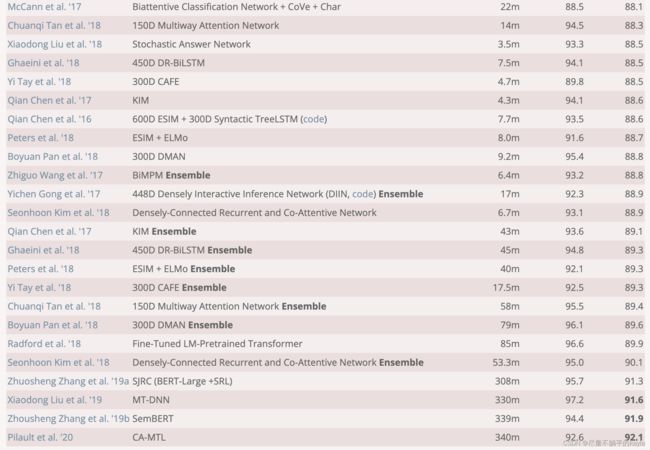
2017年的论文,在SNLI的排行榜仍榜上有名。
600D ESIM + 300D Syntactic TreeLSTM - 88.6
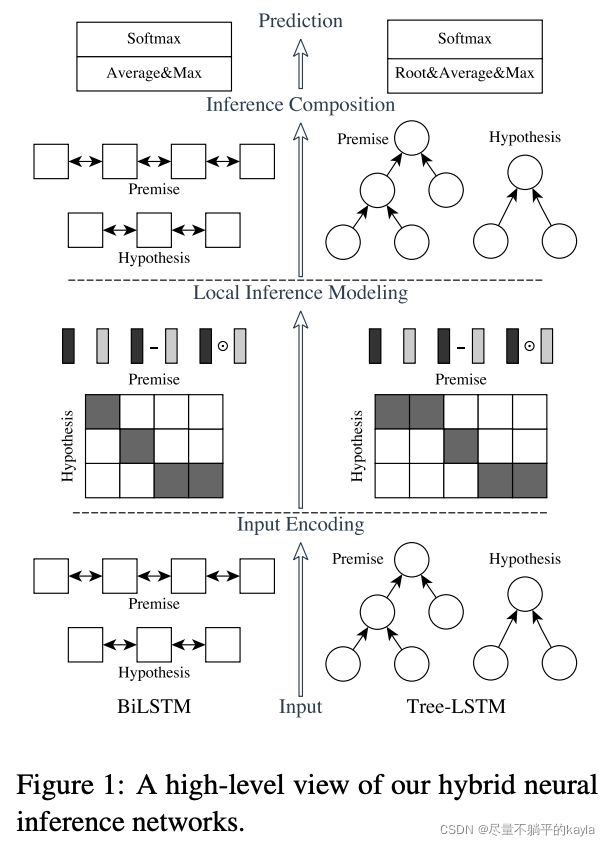
主要的组成如下图:input encoding, local inference modeling, and inference composition
input encoding
这个部分使用BiLSTM去进行编码。句子a通过BiLSTM在第i时刻的隐状态被称为 a ˉ i \bar{a}_i aˉi.
a ˉ i = B i L S T M ( a , i ) , ∀ i ∈ [ 1 , . . . , l a ] b ˉ j = B i L S T M ( b , j ) , ∀ j ∈ [ 1 , . . . , l b ] \bar{\bold{a}}_i = BiLSTM(\bold{a}, i), \forall i \in[1,...,l_a]\\\bar{\bold{b}}_j = BiLSTM(\bold{b}, j), \forall j \in[1,...,l_b] aˉi=BiLSTM(a,i),∀i∈[1,...,la]bˉj=BiLSTM(b,j),∀j∈[1,...,lb]
在每一个时刻正向LSTM和反向LSTM产生的隐状态都会进行concat,以此来表达该时刻的向量和上下文。作者同样试过GRU,发现并没有biLSTM效果好。
local inference modeling
这步是里面最重要的一步了,用到了soft attention。具体是怎么做的呢?
用 a ˉ i \bar{a}_i aˉi和 b ˉ j \bar{b}_j bˉj做点积,来求的premise和hypothesis之间的相似度。作者也试过用其他方式计算相似度,但效果不如点积。与其他只用前向LSTM的模型相比,由于这里的状态由双向LSTM生成,能够结合更多的信息。
e i j = a ˉ i T b ˉ j e_{ij} = \bar{\bold{a}}_i^T\bar{\bold{b}}_j eij=aˉiTbˉj
现在权重 e i j e_{ij} eij求出来了。但我们还要求一个权重的分布。
a ~ i = ∑ j = 1 l b e x p ( e i j ) ∑ k = 1 l b e x p ( e i k ) b ˉ j , ∀ i ∈ [ 1 , . . . , l a ] b ~ j = ∑ i = 1 l a e x p ( e i j ) ∑ k = 1 l a e x p ( e k j ) a ˉ i , ∀ j ∈ [ 1 , . . . , l b ] \tilde{\bold{a}}_i=\sum^{l_b}_{j=1}\frac{exp(e_{ij})}{\sum^{l_b}_{k=1}exp(e_{ik})} \bar{\bold{b}}_j, \forall i\in [1,...,l_a]\\\tilde{\bold{b}}_j=\sum^{l_a}_{i=1}\frac{exp(e_{ij})}{\sum^{l_a}_{k=1}exp(e_{kj})} \bar{\bold{a}}_i, \forall j\in [1,...,l_b] a~i=j=1∑lb∑k=1lbexp(eik)exp(eij)bˉj,∀i∈[1,...,la]b~j=i=1∑la∑k=1laexp(ekj)exp(eij)aˉi,∀j∈[1,...,lb]
a ~ i \tilde{\bold{a}}_i a~i是 { b ˉ j } j = 1 l b \{\bar{\bold{b}}_j\}^{l_b}_{j=1} {bˉj}j=1lb的加权和,换句话说, a ~ i \tilde{\bold{a}}_i a~i就是 { b ˉ j } j = 1 l b \{\bar{\bold{b}}_j\}^{l_b}_{j=1} {bˉj}j=1lb中关于 a ˉ i \bar{\bold{a}}_i aˉi的内容。
有了 a ~ i \tilde{\bold{a}}_i a~i和 a ˉ i \bar{\bold{a}}_i aˉi,我们希望用一种高阶的交互增强这部分local inference information。
m a = [ a ˉ ; a ~ ; a ˉ − a ~ ; a ˉ ⊙ a ~ ] m b = [ b ˉ ; b ~ ; b ˉ − b ~ ; b ˉ ⊙ b ~ ] \bold{m}_a = [\bar{\bold{a}};\tilde{\bold{a}};\bar{\bold{a}}-\tilde{\bold{a}};\bar{\bold{a}}\odot \tilde{\bold{a}}]\\\bold{m}_b = [\bar{\bold{b}};\tilde{\bold{b}};\bar{\bold{b}}-\tilde{\bold{b}};\bar{\bold{b}}\odot \tilde{\bold{b}}] ma=[aˉ;a~;aˉ−a~;aˉ⊙a~]mb=[bˉ;b~;bˉ−b~;bˉ⊙b~]
inference composition
因为不想让序列长度影响到最后结果,进行池化操作。
将 m a \bold{m}_a ma 输入到BiLSTM中再分别进行平均池化和最大池化。
v a , a v e = ∑ i = 1 l a v a , i l a , v a , m a x = max i = 1 l a v a , i v b , a v e = ∑ j = 1 l b v b , j l b , v b , m a x = max j = 1 l b v b , j v = [ v a , a v e ; v a , m a x ; v b , a v e ; v b , m a x ] \bold{v}_{a,ave}=\sum^{l_a}_{i=1}\frac{v_{a,i}}{l_a}, \bold{v}_{a,max}=\max^{l_a}_{i=1}{v_{a,i}}\\\bold{v}_{b,ave}=\sum^{l_b}_{j=1}\frac{v_{b,j}}{l_b}, \bold{v}_{b,max}=\max^{l_b}_{j=1}{v_{b,j}}\\\bold{v}=[\bold{v}_{a,ave};\bold{v}_{a,max};\bold{v}_{b,ave};\bold{v}_{b,max}] va,ave=i=1∑lalava,i,va,max=i=1maxlava,ivb,ave=j=1∑lblbvb,j,vb,max=j=1maxlbvb,jv=[va,ave;va,max;vb,ave;vb,max]
最后通过一个MLP,一层hidden layer with tanh和softmax,输出最后结果。用multiclass crossentropy计算loss。