SICE：基于CNN的多曝光图像增强网络论文解读

一、 文章摘要概述

文章题目是：
《Learning a Deep Single Image Contrast Enhancer from Multi-Exposure Images》
  这是一篇2018年图像处理领域Top之一的TIP期刊文章，针对过曝光/欠曝光的单图像对比度增强(SICE)，相较于之前的调整色调曲线以矫正输入图像的对比度不能有效增强图像细节问题，提出使用卷积神经网络(CNN)分步训练多个SICE图像增强器，在提升图像对比度同时保恢复了图像细节。为此，文章创新性的做了如下工作：

1. 建立一个大规模的多曝光图像数据集，包含多场景高分辨率图像序列。
2. 分步构建了三个基于CNN的SICE增强器，前两个是照明、细节增强网络分别提升图像对比度和细节恢复，最后一个全图增强器作为调节网络，平衡细节和纹理避免颜色失真。

二、多曝光数据采集

采集目的:

1. 数据集应包含足够高分辨率的多曝光图像序列，并涵盖不同的场景。
2. 对于每个序列，应生成高质量的参考图像，以便能够构建图像对用于端到端学习。

文中采用MEF和HDR技术来重构参考图像(文章表示有更高对比度和高可见度重构效果)，从相机拍摄到图像筛选到参考图像生成，利用1200种序列和13种MEF/HDR算法，生成了1200×13=15600种融合结果。文中经过精心筛选保留了589个高质量的参考图像和它们的相应序列。
贴出一张原图，表示一下作者挑选参考图像的艰辛历程…

三、网络构建

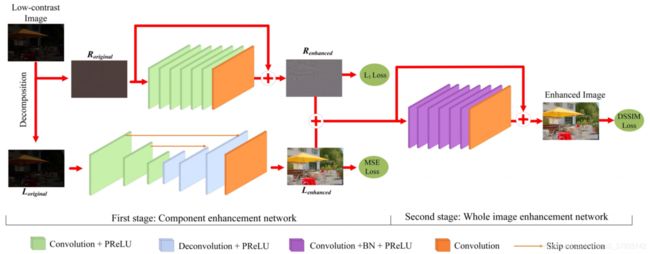
  在筛选除了优质数据集后，下面到了文章的重头戏：网络构建，根据Retinex理论，图像的低频信息表示全局自然度，高频信息表示局部细节。文章对低对比度和参考图像每分通道采用加权最小二乘法(WLS)分解为低频的照明部分 $\mathbf{L}(x,y)\in {\Re }^3$ 和高频的细节部分 $\mathbf{R}(x,y)\in {\Re }^3$，公式如下：$$\mathbf{I}(x,y)=\mathbf{L}(x,y)+\mathbf{R}(x,y)$$分解之后原始低对比度图像和参考图像就能够分别得到照明图像对和细节图像对，下面就通过两个图像对同时训练两个CNN增强器，介绍如下：

（1）、网络概览

$$整体网络结构图$$

1. Conv+PReLU: 64个3×3、5×5和9×9的滤波器，步幅为1和2，用于生成64个特征图，激活函数为PReLU(parametric rectifified linear unit)。
2. Deconv+PReLU: 64个9×9、5×5和3×3的滤波器,步幅为2和1，生成64个特征图，激活函数为PReLU。
3. Conv+BN+PReLU：64个3×3滤波器，采用批处理化(BN)，激活函数是PReLU。
4. Conv: 3个1×1大小滤波器用于重构输出。
5. Skip connection:直接Add，连接两个层的特征映射。

文中有说卷积层设置和激活函数选择的标准：
1、细节层网络的卷积和反卷积策略不仅避免了边界区域的伪影，而且减少了跨步滤波器的计算负担。
2、采用PRelu激活函数是由于训练参数有正有负且都包含输入图像的重要局部结构信息。

（2）、组件增强网络

1、Luminance Enhancement Network

  由于照明分量代表图像全局对比，所以照明网络主要重构图像对比度。文中使用：U-net 结构作为照明网络，为了增大局部感受野同时避免跨步长卷积造成细节信息的损失。
采用MSE作为损失函数，训练参数$\Theta$，公式：
$$l(\Theta )=\frac{1}{n}\sum _i^n{\Vert {\mathbf{L}}_{ref}^{(i)}-F_L({\mathbf{L}}_{original}^{(i)},\Theta )\Vert }_F^2$$网络参数表：

2、Detail Enhancement Network

  由于细节图表示图像的高频细节和边缘信息，所以细节(反射)图主要重构图像的细节特征。文章受比较经典的三篇CNN文章启发：、超分辨率的VDSR[PDF]、去噪的DnCNN[PDF]、残差学习的ResNet[PDF]（感觉这里借鉴了17年VCIP的一篇文章LLCNN，也是借鉴VSDR和ResNet），ResNet我要特地说一下，是我的偶像何恺明大神的杰作，现在稍微深层CNN网络结构一般都会有残差连接的，一方面避免了网络反向传播过程中的梯度消失问题有更高的收敛性，还通过跨层连接保证了信息的有效保留(这个在图像里面就是图像特征的跨越连接性)，避免细节信息的丢失。这和我们每个人是一样的，即使走得再远也要和之前直接联系，不能忘记了我们最初的样子，好像是这样吧！
考虑到高频细节分量通常遵循Laplace分布并包含一些噪声和异常值，文章采用L1范数作为损失函数，公式：
$$l(\Omega )=\frac{1}{n}\sum _i^n{\left|{\mathbf{R}}_{ref}^{(i)}-F_R({\mathbf{R}}_{original}^{(i)},\Omega )\right|}_1$$网络参数表：

（3）整体增强网络

  由于两个CNN网络是分别对对比度和细节进行增强的，所以不能保证合成之后整体图像质量和视觉效果。此外，由于原图的光照不均匀性，会导致合成之后的图像出现颜色失真。为了平衡图像的细节和纹理，文章又使用一个调整CNN网络将前两个网络结果合成后向参考图像学习。网络结构和细节增强网络类似，只是卷积层之后多加了一个批处理化过程，网络结构表和细节增强网络表相同。
损失函数：DSSIM(Structural dissimilarity)，它是基于SSIM的一个距离度量,训练网络参数$\Psi$，公式：
$$DSSIM(\Psi )=\frac{1}{n}\sum _i^n(1-ssim({\mathbf{I}}_{ref}^{(i)}-F({\mathbf{I}}_{input}^{(i)},\Psi )))/2$$对于两个训练阶段:
Step1:同时训练两个子网络参数$\Theta$和$\Omega$
Step2:固定$\Theta$和$\Omega$，训练调节网络参数$\Psi$
把前两个网络预训练参数作为全图增强网络的初始化，就相当于从原始低对比度图像端到端的学习其参考图像。

四、效果展示

  另外这篇文章除了与传统增强方法对比，没有使用之前优秀论文的CNN网络作为对比实验，使用直接式CNN网络(单通路单网络，只有相邻层连接)作为对比方法，虽然使用了不同的损失函数，但我觉得这个对比有一定的不充分性，可以和LLCNN对比下的个人觉得，既然是Top刊我…没什么意见，接下来看看对比实验：
  文章利用所构造的数据集，设计一个基于CNN的SICE增强器来学习低对比度输入图像 $\mathbf{I}(x,y)\in {\Re }^3$ 与其相应的参考图像 ${\mathbf{I}}_{\mathbf{r}\mathbf{e}\mathbf{f}}(x,y)\in {\Re }^3$ 。训练一个参数$W$的15层直接深度CNN网络：$H(\mathbf{I}，w)$，结构如下：

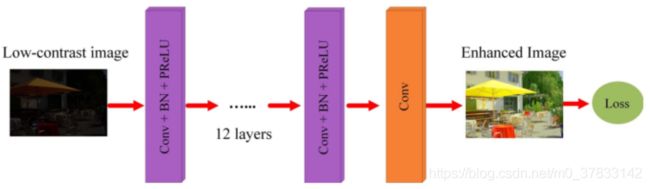
采用三种不同的损失函数：

1. MSE：
   $$l_2(W)=\frac{1}{n}\sum _i^n{\Vert {\mathbf{I}}_{ref}^{(i)}-H({\mathbf{I}}^{(i)},W)\Vert }_F^2$$
2. L1-norm:
   $$l_1(W)=\frac{1}{n}\sum _i^n{\Vert {\mathbf{I}}_{ref}^{(i)}-H({\mathbf{I}}^{(i)},W)\Vert }_1$$
3. DSSIM:
   $$DSSIM(\Psi )=\frac{1}{n}\sum _i^n(1-ssim({\mathbf{I}}_{ref}^{(i)}-H({\mathbf{I}}^{(i)},W))))/2$$
   下面展示对比实验结果：
   
   从图片可以看出直接式CNN效果其实还可以，就是图像颜色没有较好的恢复，另外我感觉三个损失函数里面L1范数对图像细节保留的较好。
     另外作者对PReLU损失函数做了一组对比实验：
   
   由于PReLU函数对负参数有保留所以对比度增强过程尽量避免了过增强现象，保持了图像较为正常的对比度信息。这个可以作为后续写文章的一个重要改进方案。
     和传统方法的对比实验在此就不在说了，那肯定是极好的鸭~

文章代码：

[论文PDF]
[Github代码]
百度云：Dataset1+Dataset2
代码编译环境：Caffa+Matlab+Cuda。目前我还在调试，有问题的小伙伴可以来互相交流~