BiLSTM之二:工程应用须知
现在有很多成熟的深度学习框架集成了BiLSTM模型,但想使用它们并非没有门槛,至少要对说明文档中的参数的释义有充分的理解。我之前写过一篇介绍BiLSTM的文章(以下用「上一篇」来指代该文章),其侧重于模型的内部结构而非工程实现,作为对该文章的补充,本文以计算BiLSTM的参数数量为切入点,再深入理解一下模型的工程实现。
建议不熟悉BiLSTM的读者在阅读本文之前先阅读上一篇文章,本文的公式及符号与该文章保持一致。
1、paddlepaddle中的LSTM模型
为叙述方便,我们将上一篇文章中的一个LSTM cell的内部结构图粘贴到此:
![]()
cell可以被翻译为“神经元”,但在LSTM的场景中容易让人误解,因为一层的LSTM模型只有一个“神经元”——这看上去似乎不够「深度学习」,所以我将不再翻译,并直接使用cell来指代这个结构。请读者仔细思考全连接神经网络中的“神经元”的概念以及此处这个cell的概念之间的区别。
观察这个cell结构,我们不难发现,整个计算中存在维度变化的地方只在于 a t − 1 a_{t-1} at−1与 X t X_t Xt的合并向量与权重相乘时。
在飞浆中,通过调用paddle.nn.LSTM类就可以实现LSTM的搭建。提醒读者注意,类的实例化是搭建神经网络结构的过程;而真正的前向计算,是通过调用该实例的forward()方法实现的。
首先,导入基础模块:
from paddle import nn
然后,实例化一个LSTM对象:
lstm = nn.LSTM(input_size=3, hidden_size=9)
上一行代码初始化了一个LSTM实例。对于LSTM类而言,只有前两个参数是必须的,即input_size和hidden_size,这里赋值分别为3和9。input_size指的是cell新输入的数据的维度,即 X t X_t Xt的维度。hidden_size指的是 X t X_t Xt(其实还有 a t − 1 a_{t-1} at−1,但它并不影响维度)经过与权重做矩阵乘法后的输出维度,这个维度完全由权重矩阵的形状决定,因此被称为“隐藏层大小”。
介绍完关键参数之后,接下来看一下参数数量是如何计算的。
2、参数的数量
首先,不考虑 a t − 1 a_{t-1} at−1和 C t − 1 C_{t-1} Ct−1的输入时,给定一个 ( 3 , 1 ) (3,1) (3,1)的输入向量,那么会得到一个 ( 9 , 1 ) (9,1) (9,1)的输出向量,其计算过程如下:
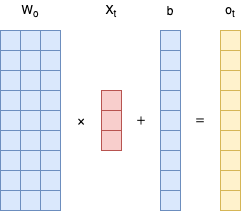
这里以「输出门」为例,直观地展现了计算过程中的维度变化情况。其他的「输入门」、「遗忘门」以及与 W W W的计算过程都是类似的。也就是说,在不考虑 a t − 1 a_{t-1} at−1和 C t − 1 C_{t-1} Ct−1的情况下,所需要的参数总量一共是:
( 3 ∗ 9 + 9 ) ∗ 4 = 144 (3*9+9)*4=144 (3∗9+9)∗4=144
在LSTM中, a t − 1 a_{t-1} at−1和 C t − 1 C_{t-1} Ct−1与 o t o_t ot具有相同的维度,在这里为9。因此, a t − 1 a_{t-1} at−1与 X t X_t Xt同时参与运算的过程如下:

此时的参数数量一共为:
( 9 ∗ 9 + 9 ∗ 1 + 9 ∗ 3 + 9 ∗ 1 ) ∗ 4 = 504 (9*9+9*1+9*3+9*1)*4=504 (9∗9+9∗1+9∗3+9∗1)∗4=504
至此,我们已经得到了单层的LSTM的参数数量的计算公式:
如果输入向量的维度为 n n n,隐藏层维度为 m m m,则参数总量为 4 ( m 2 + 2 m + m n ) 4(m^2+2m+mn) 4(m2+2m+mn)。
3、BiLSTM
如果想要构造BiLSTM,则可以在实例化LSTM类时指定direction参数:
lstm = nn.LSTM(input_size=3, hidden_size=9, direction='bidirect')
其参数数量是相同设置的LSTM的参数数量的2倍。
不同的深度学习框架基于LSTM构造BiLSTM的方法略有不同。
4、一个回归的例子
4.1 基础版本
我们不涉及任何具体的业务,也不涉及数据预处理过程,只讨论如何基于飞浆建立一个BiLSTM回归模型。
4.1.1 原始数据
首先让我们生成数据:
import numpy as np
import pandas as pd
import paddle
from paddle import nn
np.random.seed(1234)
data = np.random.random(size=(10000, 8))
df = pd.DataFrame(data, columns=[f'x{i}' for i in range(1, 8)] + ['y'])
print(df.head())
由于指定了随机数种子,输出一定是下面的内容:
x1 x2 x3 ... x6 x7 y
0 0.191519 0.622109 0.437728 ... 0.272593 0.276464 0.801872
1 0.958139 0.875933 0.357817 ... 0.712702 0.370251 0.561196
2 0.503083 0.013768 0.772827 ... 0.615396 0.075381 0.368824
3 0.933140 0.651378 0.397203 ... 0.568099 0.869127 0.436173
4 0.802148 0.143767 0.704261 ... 0.924868 0.442141 0.909316
[5 rows x 8 columns]
现在,假设我们面临的是一个价格预测问题:y是我们的目标列,表示价格;x1到x7为特征列;样本是按照时间顺序排列的。于是,我们的目标是建立一个基于BiLSTM的回归模型来对其进行预测。
4.1.2 模型修改
假设样本数据直接输入BiLSTM模型,那么它的输入大小为7,我们再定义其隐藏层的大小为32,于是,定义网络的代码为:
bilstm = LSTM(7, 32, direction="bidirect")
通过上面的分析可知,对于一个特定的样本(例如,第一行数据),利用bilstm对其进行前向计算后输出分为三部分:输出 o 0 o_0 o0,长期记忆 C 0 C_0 C0以及短期记忆 a 0 a_0 a0;其中的 C 0 C_0 C0和 a 0 a_0 a0又将和下一个样本(第二行数据)一起再进行前向计算。
这里所有的下标与python保持一致,从0开始。
如果我们指定的时间步长为5,于是,模型将重复上述过程直到它遍历到第5个样本。这时,我们会得到一个输出 o 4 o_4 o4,并将它作为这一组样本所预测的输出。
但这个输出的维度是64,再与下一个时刻的真实价格 y 5 y_5 y5计算误差前,首先需要将其变为1维。这很简单,再接一个维度为 ( 64 , 1 ) (64,1) (64,1)的全连接层即可。于是,我们计算 y ^ \hat y y^与 y 5 y_5 y5的误差后,就可以将该误差反向传播并更新网络参数了。
为了将BiLSTM网络和全连接网络连接到一起,我们可以使用「组网」的方式。它的API是paddle.nn.Sequential,基本用法是:
model = paddle.nn.Sequential(
net1,
net2,
...
)
它的作用是很直观的:将不同的网络结构堆叠起来,前面网络的输出作为后续网络的输入,从而实现快速建模。
但使用这个API的时候要注意:前一个网络的输出的形状必须与后一个网络的输入的形状一致。我们知道,BiLSTM的输出有三部分:第一部分是 y ^ \hat y y^,后面两部分存储在一个元组中,分别表示 a a a和 C C C。所以,为了能够正确地只将第一部分传入全连接网络,需要对基础的paddle提供的LSTM类进行改写:
class MyLSTM(nn.LSTM):
def __init(self, *args, **kwargs):
# 实例化时与父类保持一致
super().__init__(*args, **kwargs)
def forward(self, inputs):
# 调用父类的前向函数来计算,但只取返回结果的第一部分
output, _ = super().forward(inputs)
return output[:, -1, :] # 在第二个维度上只取最后一组值,其实就是获取最后一个时间步输出的y_hat
有的读者可能会产生一个疑问:这样修改前向运算的输出之后,第一个时间步的输出就少了 a a a和 C C C,那下一个时间步在运算时岂不是就无法捕获长短时的记忆了?
这里就需要解释一下LSTM的实现机制了。在paddle中,forward其实是在计算完所有的时间步后才一次性输出的。也就是说,假设我们的时间窗口选的是5,那么forward的第一个输出其实是包含了对应于这5个样本点的5个输出值,第二个输出的 a a a和 C C C只保留最终的状态,即各有一个值。
注意:
- 这里的「值」代表的是向量。
- 在真实的运算中还需要指定batch_size,这里默认为1,在讨论中省略,实际上即使为1也需要对在输入的第一个维度进行指定。
读者可以通过以下的代码来验证一下:
import paddle
# 用上文的data来创建一个tensor,注意这里没有留y,所以input size是8
tiny_tensor = paddle.to_tensor(data[:5], dtype=np.float32)
# 通过两次设置随机数种子,可以是lstm和mylstm的权重完全相同
paddle.seed(1234)
lstm = nn.LSTM(8, 32)
paddle.seed(1234)
mylstm = MyLSTM(8, 32)
tiny_tensor = tiny_tensor.reshape(shape=(-1, 5, 8)) # 必须指定batch_size,这里自动计算
my_out = mylstm(tiny_tensor)
out, _ = lstm(tiny_tensor)
print(my_out == out[:, -1, :])
应该打印以下内容:
Tensor(shape=[1, 32], dtype=bool, place=CPUPlace, stop_gradient=False,
[[True, True, True, True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True, True, True, True, True,
True, True, True, True, True, True, True, True]])
4.1.3 模型组网
接下来就可以进行模型组网了,非常简单:
model = nn.Sequential(
MyLSTM(7, 32, direction='bidirect', dropout=0.5),
nn.Linear(64, 1)
)
# 将模型封装
model = paddle.Model(model)
# 定义优化器、损失函数
model.prepare(paddle.optimizer.RMSProp(0.0001, parameters=model.parameters()),
paddle.nn.MSELoss())
在调用.fit()方法进行训练之前,我们还需要对训练数据进行一些封装。
4.1.4 数据的处理
在训练开始之前,还需要对数据做如下处理:
- 按照指定的时间步长转化成「序列」的形式,划分训练集测试集;
- 封装成paddle可接收的数据格式。
对于第一部分,通过以下函数可以实现:
def create_sequence(df, window: int = 5):
"""
为了能够输入LSTM模型,将数据处理成序列的形式。
假设输入的df一共有N行,那么处理后的数据的维度为:[N-window, window, 7]
"""
N = df.shape[0]
ret = np.empty(shape=(N - window, window, 7))
y = np.empty(N - window)
for i in range(N - window):
end = i + window
arr = df[['x1', 'x2', 'x3', 'x4', 'x5', 'x6', 'x7']].iloc[i: end].values
ret[i] = arr
y[i] = df['y'].iloc[i + window]
return ret, y
X, y = create_sequence(df)
接着,划分训练集与测试集:
# 按80/20的比例划分
train_size = int(train_X.shape[0] * 0.8)
test_size = train_X.shape[0] - train_size
train_X = X[:train_size]
train_y = y[:train_size]
test_X = X[-test_size:]
test_y = y[-test_size:]
对于第二部分,我们首先需要将数据转化为Tensor:
train_X_tensor = paddle.to_tensor(train_X, dtype=np.float32)
train_y_tensor = paddle.to_tensor(train_y, dtype=np.float32)
test_X_tensor = paddle.to_tensor(test_X, dtype=np.float32)
test_y_tensor = paddle.to_tensor(test_y, dtype=np.float32)
接下来,传给.fit()的训练数据需要满足一定的格式,这里是通过继承Dataset类来实现的。使用这种方法只需要重写Dataset的__getitem__和__len__方法即可:
class MyDataset(paddle.io.Dataset):
def __init__(self, dataset_type):
self.dataset_type = dataset_type
def __getitem__(self, idx):
if self.dataset_type == 'train': # 训练集的话,返回特征和标签
return train_X_tensor[idx], train_y_tensor[idx]
if self.dataset_type == 'test': # 测试集的话,返回特征
return test_X_tensor[idx]
def __len__(self):
if self.dataset_type == 'train':
return train_X_tensor.shape[0]
if self.dataset_type == 'test':
return test_X_tensor.shape[0]
最终,可以对模型进行训练了:
model.fit(MyDataset('train'), batch_size=32)
然后可以预测:
model.predict(MyDataset('test'))
当然,由于用的是随机数,结果不具备评价意义。
4.2 进阶版本
有时,作为输入的特征不止x1,...,x7,还有历史价格。
换言之,模型由:

变成了:

这对于训练过程的影响倒是不大,只需要将create_sequence函数对应的输入特征和输入维度增加,在模型组网时修改输入的维度即可。
但在预测时,问题变得有些麻烦。
我们在预测未来的多个时刻的价格时,需要逐时刻预测,并且将上一时刻的预测价格填充到下一时刻的输入特征中,因为我们没有上一时刻的真实价格数据。
目前,我没有找到paddle中关于处理这种情形的方案,因此,我对MyDataset类和预测的代码做了一些修改:
class MyDataset(Dataset):
def __init__(self, dataset_type, sub_tensor=None):
self.dataset_type = dataset_type
self.sub_tensor = sub_tensor
def __getitem__(self, idx):
# 训练时不变,但在预测时,必须逐tensor进行预测,这样才能在传入
# 模型前对输入的tensor进行价格填充
if self.dataset_type == 'train':
return train_X_tensor[idx], train_y_tensor[idx]
if self.dataset_type == 'test':
# 直接返回输入的tensor
return self.sub_tensor
def __len__(self):
if self.dataset_type == 'train':
return len(train_y_tensor)
if self.dataset_type == 'test':
# 对应的长度永远是1
return 1
同时,预测的过程也做了修改,用一个定长的队列来存储预测过的价格:
from collections import deque
last_pred = deque(maxlen=5) # 最大长度为时间窗口长度,再之前的数据对于预测下一个时刻无用
pred_value = [] # 存储预测结果
for i in range(test_X_tensor.shape[0]):
sub_tensor = test_X_tensor[i] # 获取待输入的tensor
if last_pred: # 已经存在预测结果,则将该结果填充到tensor中
num = len(last_pred)
# paddle的tensor修改貌似比较复杂,我没深入研究,采取了个笨办法
sub_array = sub_tensor.numpy()
sub_array[-num:][:,-1] = list(last_pred)
sub_tensor = paddle.to_tensor(sub_array)
res = model.predict(MyDataset('test', sub_tensor))
pred_value.append(res)
last_pred.append(res) # 更新队列
如果有其他的解决方案,欢迎评论让我知道。
参考:
- LSTM and Bidirectional LSTM for Regression
- paddlepaddle的LSTM如何写到Sequential中