RoFormer: Enhanced Transformer with Rotary Position Embedding(2021-4-20)
模型介绍
位置编码最近的Transformer模型中显的非常有效,它为位于序列不同位置的元素之间的依赖关系建模提供了有价值的监督。通过研究了不同集成位置编码信息的方法在基于transformer语言模型的学习过程的作用,提出了一种新的方法–旋转位置编码(Rotary Position Embedding,RoPE)。
具体而言,RoPE将绝对位置编码在一个旋转矩阵中,与此同时,在self-attention公式中包含了显式的相对位置依赖。尤其是,RoPE可以让有价值的属性包含在相对位置编码中,比如序列长度的灵活性、随着相对位置增加,衰减的内部token的依赖以及具备线性self-attention的能力。称使用旋转位置编码的Transformer为RoFormer,在使用不同的长文本分类数据集中,RoFormer表现的非常优秀。
模型改进
在正式介绍旋转位置编码之前,首先回顾一下transformer中的各种位置编码。
Preliminary
假设 S N = { w i } i = 1 N S_N=\{w_i\}^N_{i=1} SN={wi}i=1N表示有 N N N 个 token 的序列, w i w_i wi 表示第 i 个元素。则 S N S_N SN 对应的位置嵌入可以表示为 E N = { x i } i = 1 N E_N=\{x_i\}^N_{i=1} EN={xi}i=1N,其中 x i ∈ R d x_i \in R^d xi∈Rd 为一个token w i w_i wi d 维的没有位置信息的位置嵌入向量。self-attention首先将位置信息合并到单词嵌入中,再转换成queries、keys和values。 q m = f q ( x m , m ) q_m=f_q(x_m,m) qm=fq(xm,m) k n = f k ( x n , n ) k_n=f_k(x_n,n) kn=fk(xn,n) v n = f v ( x n , n ) v_n=f_v(x_n,n) vn=fv(xn,n)其中 q m , k n , v n q_m,k_n,v_n qm,kn,vn分别通过 f q , f k , f v f_q,f_k,f_v fq,fk,fv, 包含了第 m 个和第 n 个位置信息。然后qeury 和 key 的值用于计算注意力权重,输出是用value 表示的加权和。
a m , n = exp ( q m T k n d ) ∑ j = 1 N exp ( q m T k j d ) a_{m,n}=\displaystyle \frac {\exp(\frac {q_m^Tk_n}{\sqrt d})} {\sum^N_{j=1}\exp(\frac {q_m^Tk_j}{\sqrt d})} am,n=∑j=1Nexp(dqmTkj)exp(dqmTkn) o m = ∑ n = 1 N a m , n v n o_m=\displaystyle \sum^N_{n=1}a_{m,n}v_n om=n=1∑Nam,nvn
基于transformer位置编码的已经存在的方法主要是关注于选择一个合适的函数来生成 q m , k n , v n q_m,k_n,v_n qm,kn,vn。
Absolute position embedding
一种典型的方法为: f t : t ∈ { q , k , v } ( x i , i ) : = W t : t ∈ { q , k , v } ( x i + p i ) f_{t:t \in \{q,k,v\}}(x_i,i):=W_{t:t\in\{q,k,v\}}(x_i+p_i) ft:t∈{q,k,v}(xi,i):=Wt:t∈{q,k,v}(xi+pi)其中, p i ∈ R d p_i \in R^d pi∈Rd 是一个依赖 token x i x_i xi 位置的 d 维向量。之前的一些工作,使用的是许多可训练的向量 p i ∈ { p t } t = 1 L p_i \in \{p_t\}^L_{t=1} pi∈{pt}t=1L,其中 L L L 为可序列的最大长度。这里使用的是一个正弦函数来生成 p i p_i pi: { p i , 2 t = s i n ( k / 1000 0 2 t / d ) p i , 2 t + 1 = c o s ( k / 1000 0 2 t / d ) \begin{cases} p_{i,2t}=sin(k/10000^{2t/d}) \\ p_{i,2t+1}=cos(k/10000^{2t/d})\end{cases} {pi,2t=sin(k/100002t/d)pi,2t+1=cos(k/100002t/d)其中 p i , 2 t p_{i,2t} pi,2t 为 d d d 维向量 p i p_i pi 的第 2 t 2t 2t 个元素。从正弦函数的角度看RoPE与这种直觉知识有一定的关联。然而,除了直接的添加位置信息到表述的文本中,RoPE通过与正弦函数相乘来融合相对位置信息。
Relative position embedding
上面提到的 f q , f k , f v f_q,f_k,f_v fq,fk,fv 还有不同的形式: f q ( x m ) : = W q x m f_q(x_m):=W_qx_m fq(xm):=Wqxm f k ( x n , n ) : = W k ( x n + p ~ r k ) f_k(x_n,n):=W_k(x_n+\tilde p^k_r) fk(xn,n):=Wk(xn+p~rk) f v ( x n , n ) : = W v ( x n + p ~ r v ) f_v(x_n,n):=W_v(x_n+\tilde p^v_r) fv(xn,n):=Wv(xn+p~rv)其中, p ~ r k , p ~ r k ∈ R d \tilde p^k_r,\tilde p^k_r \in R^d p~rk,p~rk∈Rd 是一个可训练的相对位置嵌入, r = clip ( m − n , r m i n , r m a x ) r=\operatorname{clip}(m-n,r_{min},r_{max}) r=clip(m−n,rmin,rmax) 代表位置 m 和 n 的相对位置,clip 函数表示如果相对距离超过了一定距离,那么一些相对位置信息就不会使用。这样,就可以将 q m T k n q^T_mk_n qmTkn 就可以表示成: q m T k n = x m T W q T W k x n + x m T W q T W k p n + p m T W q T W k x n + p m T W q T W k p n q_m^Tk_n=x^T_mW^T_qW_kx_n+x^T_mW^T_qW_kp_n+p^T_mW^T_qW_kx_n+p^T_mW^T_qW_kp_n qmTkn=xmTWqTWkxn+xmTWqTWkpn+pmTWqTWkxn+pmTWqTWkpn一种想法就是将替换绝对位置嵌入 p n p_n pn 为正弦编码的相对位置嵌入 p ~ m − n \tilde p_{m-n} p~m−n,而第三项和第四项中的绝对位置 p m p_m pm 具有两个可训练向量 u 和 v,与查询位置无关。再者, W k W_k Wk 被区分成基于内容和基于位置的向量 x n x_n xn 和 p n p_n pn ,记为 W k W_k Wk 和 W ~ k \tilde W_k W~k。那么上式就可以写成: q m T k n = x m T W q T W k x n + x m T W q T W ~ k p ~ m − n + u T W q T W k x n + v T W q T W ~ k p ~ m − n q_m^Tk_n=x^T_mW^T_qW_kx_n+x^T_mW^T_q\tilde W_k\tilde p_{m-n}+u^TW^T_qW_kx_n+v^TW^T_q\tilde W_k \tilde p_{m-n} qmTkn=xmTWqTWkxn+xmTWqTW~kp~m−n+uTWqTWkxn+vTWqTW~kp~m−n值得注意的是,通过设置 f v ( x j ) = W v x j f_v(x_j)=W_vx_j fv(xj)=Wvxj 可以将 value 这一项的位置信息去掉。之后的一些工作只添加了相对位置编码信息到注意力权重中,比较典型的是将上式改成: q m T k n = x m T W q T W k x n + b i , j q^T_mk_n=x^T_mW^T_qW_kx_n+b_{i,j} qmTkn=xmTWqTWkxn+bi,j其中, b i , j b_{i,j} bi,j 表示可训练的偏置。研究表明, q m T k n = x m T W q T W k x n + x m T W q T W k p n + p m T W q T W k x n + p m T W q T W k p n q_m^Tk_n=x^T_mW^T_qW_kx_n+x^T_mW^T_qW_kp_n+p^T_mW^T_qW_kx_n+p^T_mW^T_qW_kp_n qmTkn=xmTWqTWkxn+xmTWqTWkpn+pmTWqTWkxn+pmTWqTWkpn 中间两项在绝对位置和单词之间几乎没有什么联系,有人提出用不同的映射矩阵来建立一对单词或者位置的模型,如下式所示: q m T k n = x m T W q T W k x n + p m T U q T U k p n + b i , j q^T_mk_n=x^T_mW^T_qW_kx_n+p^T_mU^T_qU_kp_n+b_{i,j} qmTkn=xmTWqTWkxn+pmTUqTUkpn+bi,j
但是,有研究表明 q m T k n = x m T W q T W k x n + x m T W q T W k p n + p m T W q T W k x n + p m T W q T W k p n q_m^Tk_n=x^T_mW^T_qW_kx_n+x^T_mW^T_qW_kp_n+p^T_mW^T_qW_kx_n+p^T_mW^T_qW_kp_n qmTkn=xmTWqTWkxn+xmTWqTWkpn+pmTWqTWkxn+pmTWqTWkpn 中间两项可以利用单词间的相对位置信息,结果,绝对位置嵌入 p m p_m pm 和 p n p_n pn 被简单的替换成相对位置嵌入 p ~ m − n \tilde p_{m-n} p~m−n: q m T k n = x m T W q T W k x n + x m T W q T W k p ~ m − n + p ~ m − n T W q T W k x n q^T_mk_n=x^T_mW^T_qW_kx_n+x^T_mW^T_qW_k\tilde p_{m-n} +\tilde p^T_{m-n}W^T_qW_kx_n qmTkn=xmTWqTWkxn+xmTWqTWkp~m−n+p~m−nTWqTWkxn相对位置嵌入的许多变体都和上式相似,但是上式相比其它三种相对位置编码是最有效的。总的来说,上面提到这些相对位置编码都是尝试修改 q m T k n = x m T W q T W k x n + x m T W q T W k p n + p m T W q T W k x n + p m T W q T W k p n q_m^Tk_n=x^T_mW^T_qW_kx_n+x^T_mW^T_qW_kp_n+p^T_mW^T_qW_kx_n+p^T_mW^T_qW_kp_n qmTkn=xmTWqTWkxn+xmTWqTWkpn+pmTWqTWkxn+pmTWqTWkpn 这个式子,然后直接添加位置信息到文本表述中。不一样的是, RoPE 试图在有限制的情况下修改 f q ( x m ) : = W q x m , f k ( x n , n ) : = W k ( x n + p ~ r k ) , f v ( x n , n ) : = W v ( x n + p ~ r v ) f_q(x_m):=W_qx_m,f_k(x_n,n):=W_k(x_n+\tilde p^k_r),f_v(x_n,n):=W_v(x_n+\tilde p^v_r) fq(xm):=Wqxm,fk(xn,n):=Wk(xn+p~rk),fv(xn,n):=Wv(xn+p~rv) 这三个式子,通过融入相对位置信息使这个方法有更多可解释性。
Rotary position embedding**
通常基于transformer的模型通过自注意力机制只使用了单独 token 的位置信息。从上面公式可以知道, q m T k n q^T_mk_n qmTkn 通常在单词的不同位置之间传送知识。为了融合相对位置信息,需要用一个函数 g g g 来表达 query q q q 和key k k k 之间的内积,只携带了词嵌入 x m x_m xm、 x n x_n xn,它们的相对位置 m − n m-n m−n 作为输入变量。换句话说,希望编码位置信息的内积以相对的形式出现: ⟨ f q ( x m , m ) , f k ( x n , n ) ⟩ = g ( x m , x n , m − n ) \braket {f_q(x_m,m),f_k(x_n,n)}=g(x_m,x_n,m-n) ⟨fq(xm,m),fk(xn,n)⟩=g(xm,xn,m−n)最终的目标就是找一个编码机制使函数 f q ( x m , m ) f_q(x_m,m) fq(xm,m) 和 f k ( x n , n ) f_k(x_n,n) fk(xn,n) 符合上述的形式。
A 2D case
在一个简单的例子中,维度 d = 2 d=2 d=2。在这种条件下,在一个二维平面上充分利用向量的几何属性,使用向量的复数形式作为解决方案,这样用公式可以表示为: f q ( x m , m ) = ( W q x m ) e i m θ f_q(x_m,m)=(W_qx_m)e^{im\theta} fq(xm,m)=(Wqxm)eimθ f k ( x n , n ) = ( W k x n ) e i n θ f_k(x_n,n)=(W_kx_n)e^{in\theta} fk(xn,n)=(Wkxn)einθ g ( x m , x n , m − n ) = Re [ ( W q x m ) ( W k x n ) ∗ e i ( m − n ) θ ] g(x_m,x_n,m-n)=\operatorname{Re}[(W_qx_m)(W_kx_n)^*e^{i(m-n)\theta}] g(xm,xn,m−n)=Re[(Wqxm)(Wkxn)∗ei(m−n)θ]其中,Re[ ⋅ \cdot ⋅] 为复数的实数部分, ( W k x n ) ∗ (W_kx_n)^* (Wkxn)∗ 表示 ( W k x n ) (W_kx_n) (Wkxn) 的共轭复数, θ ∈ R \theta \in R θ∈R 为一个预置的非0常数。这样,就可以将 f { q , k } f_{\{q,k\}} f{q,k} 写成一个乘法矩阵形式:
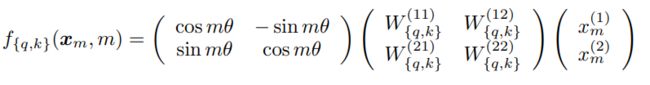
其中, ( x m ( 1 ) (x^{(1)}_m (xm(1), x m ( 2 ) ) x^{(2)}_m) xm(2)) 为 x m x_m xm 的二维坐标表示。相似的, g g g 可以视为一个矩阵,在二维条件下,可以求解公式 ⟨ f q ( x m , m ) , f k ( x n , n ) ⟩ = g ( x m , x n , m − n ) \braket {f_q(x_m,m),f_k(x_n,n)}=g(x_m,x_n,m-n) ⟨fq(xm,m),fk(xn,n)⟩=g(xm,xn,m−n)。具体而言,合并相对位置嵌入是很简单的,只需要简单的将仿射变换词嵌入向量按其位置索引的角度倍数旋转即可,从而解释了旋转位置嵌入背后的直觉。
General form
为了将结果 x i x_i xi 从二维推广到任何维度 d(d为偶数),将 d 维空间分成 d/2 子空间,并结合内积线性的优点,将 f { q , k } f_{\{q,k\}} f{q,k} 变成: f { q , k } ( x m , m ) = R Θ , m d W { q , k } x m f_{\{q,k\}}(x_m,m)=R^d_{\Theta,m}W_{\{q,k\}}x_m f{q,k}(xm,m)=RΘ,mdW{q,k}xm
where
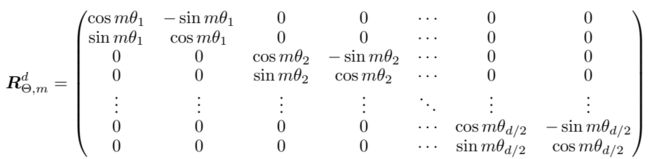
其中, R Θ , m d R^d_{\Theta,m} RΘ,md 是一个预定义参数 Θ = { θ i = 1000 0 − 2 ( i − 1 ) / d , i ∈ [ 1 , 2 , . . . , d / 2 ] } \Theta={\{\theta_i=10000^{-2(i-1)/d},i \in[1,2,...,d/2]\}} Θ={θi=10000−2(i−1)/d,i∈[1,2,...,d/2]}的旋转矩阵。将 RoPE 应用到自注意力中,得到: q m T k n = ( R Θ , m d W q x m ) T ( R Θ , m d W k x n ) = x T W q R Θ , n − m d W k x n q_m^Tk_n=(R^d_{\Theta,m}W_qx_m)^T(R^d_{\Theta,m}W_kx_n)=x^TW_qR^d_{\Theta,n-m}W_kx_n qmTkn=(RΘ,mdWqxm)T(RΘ,mdWkxn)=xTWqRΘ,n−mdWkxn其中, R Θ , n − m d = ( R Θ , m d ) T R Θ , n d R^d_{\Theta,n-m}=(R^d_{\Theta,m})^TR^d_{\Theta,n} RΘ,n−md=(RΘ,md)TRΘ,nd。注意, R Θ d R^d_{\Theta} RΘd 是一个正交矩阵,确保位置信息编码过程的稳定性。此外,由于 R Θ d R^d_{\Theta} RΘd的稀疏性,在上式中直接应用矩阵乘法并不是有效的,在后面提供了另外一种实现方式。
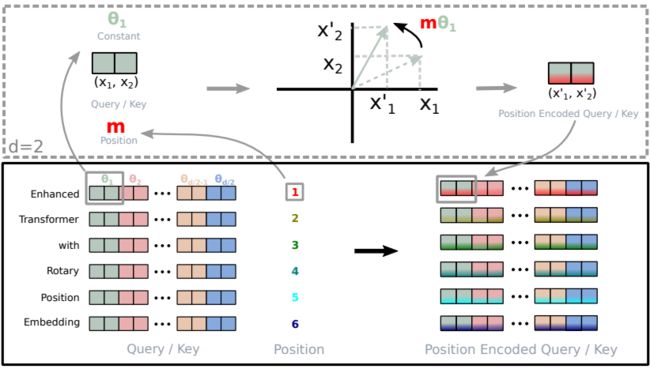
与以往工作中所采用的位置嵌入方法(加法)不同,RoPE使用的是乘法。当应用于self-attention时,RoPE通过旋转矩阵乘积自然地合并了相对位置信息,而不是改变加法位置编码改变公式中的项。
下图展示了RoPE的具体实现细节:
Properties of RoPE
长期的衰减(Long-term decay):当设置 θ i = 1000 0 − 2 i / d \theta_i=10000^{-2i/d} θi=10000−2i/d 时,可以证明这样设置会出现一个长期的衰减,意味着当距离增加时内积就会衰减。这个性质与相对距离较长的一对标记之间的联系更少的直觉相一致。
线性注意力的RoPE(RoPE with linear attention):self-attention 可以用一种更一般的形式来改写:

原来的 self-attention 选择 sim ( q m , k n ) = exp ( q m T k n / d ) \operatorname{sim}(q_m,k_n)=\exp(q_m^Tk_n/\sqrt d) sim(qm,kn)=exp(qmTkn/d),注意,最初的self-attention 应该为每一对 token 计算 query 和 key 的内积,时间复杂度为 O ( n 2 ) O(n^2) O(n2)。改写后的线性注意力可以写成:
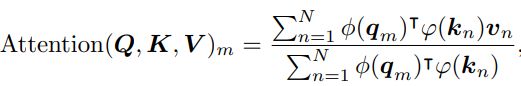
其中, ϕ ( ⋅ ) \phi(\cdot) ϕ(⋅) 和 φ ( ⋅ ) \varphi(\cdot) φ(⋅) 通常是非负函数。有人提出 ϕ ( x ) = φ ( x ) = e l u ( x ) + 1 \phi(x)=\varphi(x)=elu(x)+1 ϕ(x)=φ(x)=elu(x)+1,首先使用矩阵乘法的结合律计算键和值之间的积。在进行内积之前,使用softmax 函数来分别规范化query 和 key,相当于 ϕ ( q i ) = softmax ( q i ) , ϕ ( k j ) = exp ( k j ) \phi(q_i)=\operatorname{softmax}(q_i),\phi(k_j)=\exp(k_j) ϕ(qi)=softmax(qi),ϕ(kj)=exp(kj)。由于RoPE通过旋转注入位置信息,保持隐状态的形式不变,可以通过旋转矩阵与非负函数的输出相乘,将RoPE与线性注意结合起来。
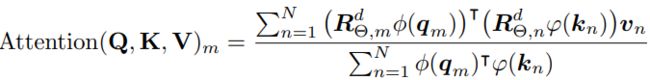
值得注意的是,保持分母不变,以避免除零的风险,分子的和可能包含负项。尽管每个 value v i v_i vi 的权重不是严格的概率规范化,但是可以善意地认为,计算仍然可以突出 values 的重要性。
直接用矩阵乘法来实现会很浪费算力,推荐通过下述方式来实现RoPE:
模型参考
论文地址:https://arxiv.org/abs/2104.09864
代码地址1:https://github.com/lucidrains/performer-pytorch
代码地址2:https://github.com/ZhuiyiTechnology/roformer