人工智能-聚类算法（分级聚类）

题目描述：

在二维平面根据一定特点产生一些点，然后给定标签，之后生成txt文档数据。

生成数据代码：

import random
import numpy as np
import matplotlib.pyplot as plt

import numpy as np
import matplotlib.pyplot as plt





def genConCircle(filePath, r1, r2, eps):
    """
    :param filePath:
    :param r1:
    :param r2:
    :param eps:
    :return:
    """
    x1 = np.linspace(-5, 5, num=200)
    y1 = 0.5* x1 + [np.random.random() for _ in range(200)]+5
    x2 = np.linspace(-5, 5, num=200)
    y2 = -0.5 * x2 + [np.random.random() for _ in range(200)]-5.5
    def getRandom(r1, eps):
        return r1 + eps * r1 * random.random() - 0.5 * eps * r1

    with open(filePath, 'w+') as f:
        for i in np.arange(0, 2 * np.pi, 0.01 * np.pi):
            f.write('{} {} {}\n'.format(getRandom(r1, eps) * np.cos(i), getRandom(r1, eps) * np.sin(i),1))
        for i in np.arange(0, 2 * np.pi, 0.01 * np.pi):
            f.write('{} {} {}\n'.format(getRandom(r2, eps) * np.cos(i), getRandom(r2, eps) * np.sin(i),2))
        for i in range(200):
            f.write('{} {} {}\n'.format(x1[i], y1[i],3))
        for i in range(200):
            f.write('{} {} {}\n'.format(x2[i], y2[i],4))




def draw2DTxt(filePath):
    data = np.loadtxt(filePath)
    print(data)
    x = data[:, 0]
    y = data[:, 1]
    plt.scatter(x[0:200], y[0:200],c='b')
    plt.scatter(x[200:400], y[200:400], c='r')
    plt.scatter(x[400:600], y[400:600], c='y')
    plt.scatter(x[600:800], y[600:800], c='g')
    plt.show()


if __name__ == '__main__':
    genConCircle('a.txt', 2.5, 3.5, 0.2)
    draw2DTxt('a.txt')

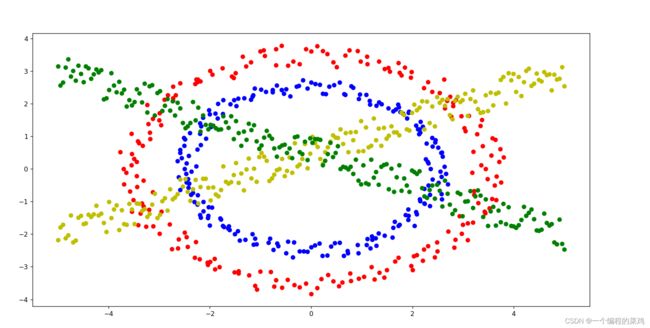
数据分布情况如下：

 

之后对产生的数据进行分级聚类

分级聚类的代码：

import math
import pandas
import matplotlib.pyplot as plt
import numpy as np



def readfile(filename):
    """处理文件数据"""
    lines = [line for line in open(filename)]
    rownames = []
    data = []
    for line in lines:
        p = line.strip()
        p=p.split()
        rownames.append(p[-1])
        data.append([float(x) for x in p[0:2]])
    return rownames,  data



# 利用皮尔逊相关度作相关性判断
# 传入的参数为两个list
def person(v1, v2):
    # 简单求和
    sum1 = sum(v1)
    sum2 = sum(v2)
    # 求平方和
    sum1Sq = sum([pow(v, 2) for v in v1])
    sum2Sq = sum([pow(v, 2) for v in v2])
    # 求乘积之和
    pSum = sum([v1[i] * v2[i] for i in range(len(v1))])
    # 计算r
    num = pSum - (sum1 * sum2 / len(v1))
    den = math.sqrt((sum1Sq - pow(sum1, 2) / len(v1)) * (sum2Sq - pow(sum2, 2) / len(v1)))
    if den == 0: return 0
    # 让相似度越大的两个元素之间的距离变得更小
    return 1.0 - num / den

def distEuclid(x, y):
    x=np.array(x)
    y=np.array(y)
    return np.sqrt(np.sum((x - y) ** 2))

# 代表层级数
class bicluster:
    """标记类属性"""
    def __init__(self, vec, left=None, right=None, distance=0.0, id_number=None,information=None,new_vec=None):
        self.left = left
        self.right = right
        self.vec = vec
        self.id_number = id_number
        self.distance = distance
        self.information=information
        self.new_vec=new_vec

# 聚类算法（直到聚为1类才停止）
def hcluster(rows,rowsname, distance=person):
    """分级聚类"""
    distances = {}
    clust=[]
    currentclustid = -1
    # 最开始的聚类就是数据集中的行 有多少行就有多少类
    for i in range(len(rows)):
        clust.append(bicluster(rows[i],id_number=i,information=[rowsname[i]],new_vec=[rows[i]]))
    while len(clust) > 4:  #聚类为三类
        lowstpair = (0, 1)
        closest = distance(clust[0].vec, clust[1].vec)
        new_information=[]
        new_vecs=[]
        # 遍历每一个配对，寻找最小
        for i in range(len(clust)):
            for j in range(i + 1, len(clust)):
                # 用distances来缓存距离的计算值
                if (clust[i].id_number, clust[j].id_number) not in distances:
                    distances[(clust[i].id_number, clust[j].id_number)] = distEuclid(clust[i].vec, clust[j].vec)
                d = distances[(clust[i].id_number, clust[j].id_number)]
                if d < closest:
                    closest = d
                    lowstpair = (i, j)
        ans1=clust[lowstpair[0]].information
        ans2=clust[lowstpair[1]].information
        new_information=new_information+ans1
        new_information=new_information+ans2

        ans3 = clust[lowstpair[0]].new_vec
        ans4 = clust[lowstpair[1]].new_vec
        new_vecs= new_vecs+ ans3
        new_vecs = new_vecs + ans4
        #print(new_information)
        # 计算两个聚类的平均值
        mergevec = [(clust[lowstpair[0]].vec[i] + clust[lowstpair[1]].vec[i]) / 2.0 for i in range(len(clust[0].vec))]
        # 建立新的聚类
        newcluster = bicluster(mergevec, left=clust[lowstpair[0]], right=clust[lowstpair[1]], distance=closest,id_number=currentclustid,information=new_information,new_vec=new_vecs)
        #print(newcluster)
        # 不在原来集合中的聚类，其id为负数
        currentclustid -= 1
        # 先删右边的则不会对左边的产生影响
        del clust[lowstpair[1]]
        del clust[lowstpair[0]]
        clust.append(newcluster)
    return clust

def showdata(ans):
    '''画图的展示'''
    x1 = []
    y1 = []
    for i in range(len(ans[0].new_vec)):
        x1.append(ans[0].new_vec[i][0])
        y1.append(ans[0].new_vec[i][1])
    x2 = []
    y2 = []
    for i in range(len(ans[1].new_vec)):
        x2.append(ans[1].new_vec[i][0])
        y2.append(ans[1].new_vec[i][1])
    x3 = []
    y3 = []
    for i in range(len(ans[2].new_vec)):
        x3.append(ans[2].new_vec[i][0])
        y3.append(ans[2].new_vec[i][1])
    x4 = []
    y4 = []
    for i in range(len(ans[3].new_vec)):
        x4.append(ans[3].new_vec[i][0])
        y4.append(ans[3].new_vec[i][1])
    plt.scatter(x1, y1, c='r', s=20, alpha=0.9)
    plt.scatter(x2, y2, c='b', s=20, alpha=0.9)
    plt.scatter(x3, y3, c='g', s=20, alpha=0.9)
    plt.scatter(x4, y4, c='y', s=20, alpha=0.9)
    plt.show()

def get_test(ans,k,total_num):
    '''准确率计算函数'''
    num=0
    for i in range(k):
        data=ans[i].information
        label=max(data, key=data.count)
        num=num+data.count(label)
    pass
    print("准确率为：")
    print(num/total_num)


a,b=readfile('data_test3')
total_num=len(b)
ans=hcluster(b,a, distance=person)
get_test(ans,4,total_num)
showdata(ans)

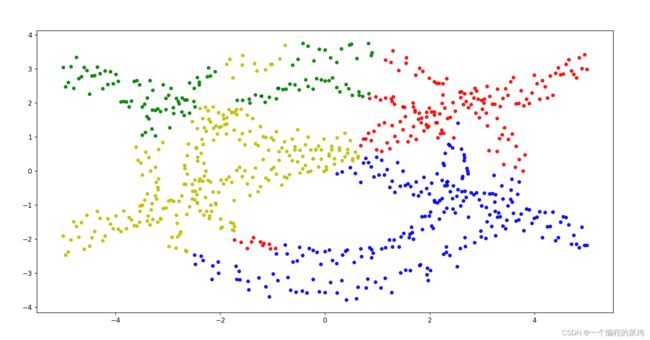
下面是分级聚类的结果：

可以看到分级聚类的效果并不是很好，其实这一类数据更加适合基于密度的聚类，比如：密度峰值，高斯，均值漂移