【算法面试题汇总】LeetBook列表的算法面试题汇总---树题目及答案

整理不易留个小心心呗
如果有更好的或者是我有错的地方还请各位大佬指出哦
有些是copy的还望不要介意

二叉搜索树中第k小的元素

题目描述：
给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 个最小元素（从 1 开始计数）。

示例：

输入：root = [3,1,4,null,2], k = 1
输出：1

• 中序遍历

  时间O(H+k) 树是平衡树时O(logN+k),树是线性树时O(N+k)(树中每个结点只有一个或没有子节点)

  空间O(H) 树是平衡树时O(logN)，树是线性树时O(H)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int kthSmallest(TreeNode root, int k) {
        Deque<TreeNode> stack = new ArrayDeque<>();
        while(root!=null || !stack.isEmpty()){
            while(root!=null){
                stack.push(root);
                root = root.left;
            }
            root = stack.pop();
            --k;
            //找到答案后便停止遍历，防止遍历整颗树
            if(k == 0){
                break;
            }
            root = root.right;
        }
        return root.val;
    }
}

进阶:如果二叉搜索树经常被修改（插入/删除操作）并且你需要频繁地查找第 k 小的值，你将如何优化算法？

• 哈希表

  利用哈希表记录每个结点的子树结点树，便不用在遍历子树

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int kthSmallest(TreeNode root, int k) {
        MyBst bst = new MyBst(root);
        return bst.kthSmallest(k);
    }
}

class MyBst{
    TreeNode root;
    //记录每个结点为根结点的子树的结点树
    Map<TreeNode,Integer> map;

    public MyBst(TreeNode root){
        this.root = root;
        this.map = new HashMap<>();
        countNodeNum(root);
    }

    //返回二叉搜索树中第k小的元素
    public int kthSmallest(int k){
        TreeNode node = root;
        while(node!=null){
            int left = getNodeNum(node.left);
            if(left < k-1){
                //第k小的元素在右子树中
                node = node.right;
                k -= left+1;
            }else if(left == k-1){
                //该结点便是第k小的元素
                break;
            }else{
                //第k小的元素就在左子树中
                node = node.left;
            }
        }
        return node.val;
    }

    //统计以node为根节点的子树的结点树
    private int countNodeNum(TreeNode node){
        if(node == null){
            return 0;
        }
        map.put(node,1+countNodeNum(node.left)+countNodeNum(node.right));
        return map.get(node);
    }

    private int getNodeNum(TreeNode node){
        return map.getOrDefault(node,0);
    }
}

• 平衡二叉树*

class Solution {
    public int kthSmallest(TreeNode root, int k) {
        // 中序遍历生成数值列表
        List<Integer> inorderList = new ArrayList<Integer>();
        inorder(root, inorderList);

        // 构造平衡二叉搜索树
        AVL avl = new AVL(inorderList);

        // 模拟1000次插入和删除操作
        int[] randomNums = new int[1000];
        Random random = new Random();
        for (int i = 0; i < 1000; ++i) {
            randomNums[i] = random.nextInt(10001);
            avl.insert(randomNums[i]);
        }
        shuffle(randomNums); // 列表乱序
        for (int i = 0; i < 1000; ++i) {
            avl.delete(randomNums[i]);
        }

        return avl.kthSmallest(k);
    }

    private void inorder(TreeNode node, List<Integer> inorderList) {
        if (node.left != null) {
            inorder(node.left, inorderList);
        }
        inorderList.add(node.val);
        if (node.right != null) {
            inorder(node.right, inorderList);
        }
    }

    private void shuffle(int[] arr) {
        Random random = new Random();
        int length = arr.length;
        for (int i = 0; i < length; i++) {
            int randIndex = random.nextInt(length);
            int temp = arr[i];
            arr[i] = arr[randIndex];
            arr[randIndex] = temp;
        }
    }
}

// 平衡二叉搜索树（AVL树）：允许重复值
class AVL {
    Node root;

    // 平衡二叉搜索树结点
    class Node {
        int val;
        Node parent;
        Node left;
        Node right;
        int size;
        int height;

        public Node(int val) {
            this(val, null);
        }

        public Node(int val, Node parent) {
            this(val, parent, null, null);
        }

        public Node(int val, Node parent, Node left, Node right) {
            this.val = val;
            this.parent = parent;
            this.left = left;
            this.right = right;
            this.height = 0; // 结点高度：以node为根节点的子树的高度（高度定义：叶结点的高度是0）
            this.size = 1; // 结点元素数：以node为根节点的子树的节点总数
        }
    }

    public AVL(List<Integer> vals) {
        if (vals != null) {
            this.root = build(vals, 0, vals.size() - 1, null);
        }
    }

    // 根据vals[l:r]构造平衡二叉搜索树 -> 返回根结点
    private Node build(List<Integer> vals, int l, int r, Node parent) {
        int m = (l + r) >> 1;
        Node node = new Node(vals.get(m), parent);
        if (l <= m - 1) {
            node.left = build(vals, l, m - 1, node);
        }
        if (m + 1 <= r) {
            node.right = build(vals, m + 1, r, node);
        }
        recompute(node);
        return node;
    }

    // 返回二叉搜索树中第k小的元素
    public int kthSmallest(int k) {
        Node node = root;
        while (node != null) {
            int left = getSize(node.left);
            if (left < k - 1) {
                node = node.right;
                k -= left + 1;
            } else if (left == k - 1) {
                break;
            } else {
                node = node.left;
            }
        }
        return node.val;
    }

    public void insert(int v) {
        if (root == null) {
            root = new Node(v);
        } else {
            // 计算新结点的添加位置
            Node node = subtreeSearch(root, v);
            boolean isAddLeft = v <= node.val; // 是否将新结点添加到node的左子结点
            if (node.val == v) { // 如果值为v的结点已存在
                if (node.left != null) { // 值为v的结点存在左子结点，则添加到其左子树的最右侧
                    node = subtreeLast(node.left);
                    isAddLeft = false;
                } else { // 值为v的结点不存在左子结点，则添加到其左子结点
                    isAddLeft = true;
                }
            }

            // 添加新结点
            Node leaf = new Node(v, node);
            if (isAddLeft) {
                node.left = leaf;
            } else {
                node.right = leaf;
            }

            rebalance(leaf);
        }
    }

    // 删除值为v的结点 -> 返回是否成功删除结点
    public boolean delete(int v) {
        if (root == null) {
            return false;
        }

        Node node = subtreeSearch(root, v);
        if (node.val != v) { // 没有找到需要删除的结点
            return false;
        }

        // 处理当前结点既有左子树也有右子树的情况
        // 若左子树比右子树高度低，则将当前结点替换为右子树最左侧的结点，并移除右子树最左侧的结点
        // 若右子树比左子树高度低，则将当前结点替换为左子树最右侧的结点，并移除左子树最右侧的结点
        if (node.left != null && node.right != null) {
            Node replacement = null;
            if (node.left.height <= node.right.height) {
                replacement = subtreeFirst(node.right);
            } else {
                replacement = subtreeLast(node.left);
            }
            node.val = replacement.val;
            node = replacement;
        }

        Node parent = node.parent;
        delete(node);
        rebalance(parent);
        return true;
    }

    // 删除结点p并用它的子结点代替它，结点p至多只能有1个子结点
    private void delete(Node node) {
        if (node.left != null && node.right != null) {
            return;
            // throw new Exception("Node has two children");
        }
        Node child = node.left != null ? node.left : node.right;
        if (child != null) {
            child.parent = node.parent;
        }
        if (node == root) {
            root = child;
        } else {
            Node parent = node.parent;
            if (node == parent.left) {
                parent.left = child;
            } else {
                parent.right = child;
            }
        }
        node.parent = node;
    }

    // 在以node为根结点的子树中搜索值为v的结点，如果没有值为v的结点，则返回值为v的结点应该在的位置的父结点
    private Node subtreeSearch(Node node, int v) {
        if (node.val < v && node.right != null) {
            return subtreeSearch(node.right, v);
        } else if (node.val > v && node.left != null) {
            return subtreeSearch(node.left, v);
        } else {
            return node;
        }
    }

    // 重新计算node结点的高度和元素数
    private void recompute(Node node) {
        node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
        node.size = 1 + getSize(node.left) + getSize(node.right);
    }

    // 从node结点开始（含node结点）逐个向上重新平衡二叉树，并更新结点高度和元素数
    private void rebalance(Node node) {
        while (node != null) {
            int oldHeight = node.height, oldSize = node.size;
            if (!isBalanced(node)) {
                node = restructure(tallGrandchild(node));
                recompute(node.left);
                recompute(node.right);
            }
            recompute(node);
            if (node.height == oldHeight && node.size == oldSize) {
                node = null; // 如果结点高度和元素数都没有变化则不需要再继续向上调整
            } else {
                node = node.parent;
            }
        }
    }

    // 判断node结点是否平衡
    private boolean isBalanced(Node node) {
        return Math.abs(getHeight(node.left) - getHeight(node.right)) <= 1;
    }

    // 获取node结点更高的子树
    private Node tallChild(Node node) {
        if (getHeight(node.left) > getHeight(node.right)) {
            return node.left;
        } else {
            return node.right;
        }
    }

    // 获取node结点更高的子树中的更高的子树
    private Node tallGrandchild(Node node) {
        Node child = tallChild(node);
        return tallChild(child);
    }

    // 重新连接父结点和子结点（子结点允许为空）
    private static void relink(Node parent, Node child, boolean isLeft) {
        if (isLeft) {
            parent.left = child;
        } else {
            parent.right = child;
        }
        if (child != null) {
            child.parent = parent;
        }
    }

    // 旋转操作
    private void rotate(Node node) {
        Node parent = node.parent;
        Node grandparent = parent.parent;
        if (grandparent == null) {
            root = node;
            node.parent = null;
        } else {
            relink(grandparent, node, parent == grandparent.left);
        }

        if (node == parent.left) {
            relink(parent, node.right, true);
            relink(node, parent, false);
        } else {
            relink(parent, node.left, false);
            relink(node, parent, true);
        }
    }

    // trinode操作
    private Node restructure(Node node) {
        Node parent = node.parent;
        Node grandparent = parent.parent;

        if ((node == parent.right) == (parent == grandparent.right)) { // 处理需要一次旋转的情况
            rotate(parent);
            return parent;
        } else { // 处理需要两次旋转的情况：第1次旋转后即成为需要一次旋转的情况
            rotate(node);
            rotate(node);
            return node;
        }
    }

    // 返回以node为根结点的子树的第1个元素
    private static Node subtreeFirst(Node node) {
        while (node.left != null) {
            node = node.left;
        }
        return node;
    }

    // 返回以node为根结点的子树的最后1个元素
    private static Node subtreeLast(Node node) {
        while (node.right != null) {
            node = node.right;
        }
        return node;
    }

    // 获取以node为根结点的子树的高度
    private static int getHeight(Node node) {
        return node != null ? node.height : 0;
    }

    // 获取以node为根结点的子树的结点数
    private static int getSize(Node node) {
        return node != null ? node.size : 0;
    }
}

作者：LeetCode-Solution
链接：https://leetcode.cn/problems/kth-smallest-element-in-a-bst/solution/er-cha-sou-suo-shu-zhong-di-kxiao-de-yua-8o07/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

二叉树的最近公共祖先

题目描述：
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”
所有 Node.val 互不相同 。

示例：

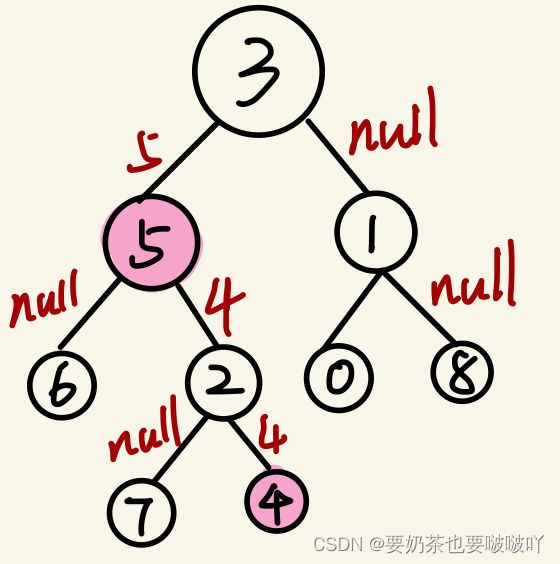
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

• 代码实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == p || root == q || root==null)return root;
        //查看左右子树中是否包含pq结点
        TreeNode left = lowestCommonAncestor(root.left,p,q);
        TreeNode right = lowestCommonAncestor(root.right,p,q);
        //都不为空则pq在异侧，则root为目标结点
        if(left != null && right != null){
            return root;
        }else if(left == null){
            //都在右子树中
            return right;
        }else if(right == null){
            //都在左子树中
            return left;
        }else{
            //左右子树都为空，说明不包含pq
            return null;
        }
    }
}

二叉树的序列化与反序列化

题目描述：
序列化是将一个数据结构或者对象转换为连续的比特位的操作，进而可以将转换后的数据存储在一个文件或者内存中，同时也可以通过网络传输到另一个计算机环境，采取相反方式重构得到原数据。
请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑，你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。

提示: 输入输出格式与 LeetCode 目前使用的方式一致，详情请参阅 LeetCode 序列化二叉树的格式。你并非必须采取这种方式，你也可以采用其他的方法解决这个问题。

示例：

输入：root = [1,2,3,null,null,4,5]
输出：[1,2,3,null,null,4,5]

• 先序遍历

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
public class Codec {

    // Encodes a tree to a single string.
    public String serialize(TreeNode root) {
        if(root == null)return "null";
        return root.val + "," +
                serialize(root.left) + ","+
                serialize(root.right);
    }

    // Decodes your encoded data to tree.
    public TreeNode deserialize(String data) {
        String[] s = data.split(",");
        List<String> r = new ArrayList<>(Arrays.asList(s));
        return dfs(r);
    }

    public TreeNode dfs(List<String> r){
        if("null".equals(r.get(0))){
            r.remove(0);
            return null;
        }
        TreeNode node = new TreeNode(Integer.valueOf(r.get(0)));
        r.remove(0);
        node.left = dfs(r);
        node.right = dfs(r);
        return node;
    }
}

// Your Codec object will be instantiated and called as such:
// Codec ser = new Codec();
// Codec deser = new Codec();
// TreeNode ans = deser.deserialize(ser.serialize(root));

• 后序遍历

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
public class Codec {

    // Encodes a tree to a single string.
    public String serialize(TreeNode root) {
        if(root == null)return "null";
        return serialize(root.left) + "," +
                serialize(root.right) + ","+
                root.val;
    }

    // Decodes your encoded data to tree.
    public TreeNode deserialize(String data) {
        String[] s = data.split(",");
        List<String> r = new ArrayList<>(Arrays.asList(s));
        return dfs(r);
    }

    public TreeNode dfs(List<String> r){
        if("null".equals(r.get(r.size()-1))){
            r.remove(r.size()-1);
            return null;
        }
        TreeNode node = new TreeNode(Integer.valueOf(r.get(r.size()-1)));
        r.remove(r.size()-1);
        node.right = dfs(r);
        node.left = dfs(r);
        return node;
    }
}

// Your Codec object will be instantiated and called as such:
// Codec ser = new Codec();
// Codec deser = new Codec();
// TreeNode ans = deser.deserialize(ser.serialize(root));

• 层次遍历

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
public class Codec {

    // Encodes a tree to a single string.
    public String serialize(TreeNode root) {
        if(root==null){
            return "";
        }
        List res = new ArrayList<>();
        Deque<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while(!queue.isEmpty()){
            TreeNode node = queue.poll();
            if(node==null){
                res.add("null");
                continue;
            }else{
                res.add(node.val);
                queue.add(node.left);
                queue.add(node.right);
            }
        }
        StringBuilder s = new StringBuilder();
        for(int i=0;i<res.size();i++){
            s.append(res.get(i));
            if(i<res.size()-1) s.append(",");
        }
        return s.toString();
    }


    // Decodes your encoded data to tree.
    public TreeNode deserialize(String data) {
        if(data.length()==0)return null;
        String[] s = data.split(",");
        Deque<TreeNode> queue = new LinkedList<>();
        TreeNode root = new TreeNode(Integer.valueOf(s[0]));
        queue.add(root);
        int index = 1;
        while(index<s.length){
            TreeNode node = queue.poll();
            if(!("null".equals(s[index]))){
                node.left = new TreeNode(Integer.valueOf(s[index]));
                queue.add(node.left);
            }
            index++;
            if(!("null".equals(s[index]))){
                node.right = new TreeNode(Integer.valueOf(s[index]));
                queue.add(node.right);
            }
            index++;
        }
        return root;
    }
}

// Your Codec object will be instantiated and called as such:
// Codec ser = new Codec();
// Codec deser = new Codec();
// TreeNode ans = deser.deserialize(ser.serialize(root));

中序遍历结果不唯一

天际线问题**

题目描述：
城市的 天际线 是从远处观看该城市中所有建筑物形成的轮廓的外部轮廓。给你所有建筑物的位置和高度，请返回 由这些建筑物形成的 天际线 。
每个建筑物的几何信息由数组 buildings 表示，其中三元组 buildings[i] = [lefti, righti, heighti] 表示：

lefti 是第 i 座建筑物左边缘的 x 坐标。
righti 是第 i 座建筑物右边缘的 x 坐标。
heighti 是第 i 座建筑物的高度。

你可以假设所有的建筑都是完美的长方形，在高度为 0 的绝对平坦的表面上。

天际线 应该表示为由 “关键点” 组成的列表，格式 [[x1,y1],[x2,y2],…] ，并按 x 坐标 进行 排序 。关键点是水平线段的左端点。列表中最后一个点是最右侧建筑物的终点，y 坐标始终为 0 ，仅用于标记天际线的终点。此外，任何两个相邻建筑物之间的地面都应被视为天际线轮廓的一部分。

注意：输出天际线中不得有连续的相同高度的水平线。例如 […[2 3], [4 5], [7 5], [11 5], [12 7]…] 是不正确的答案；三条高度为 5 的线应该在最终输出中合并为一个：[…[2 3], [4 5], [12 7], …]

示例：

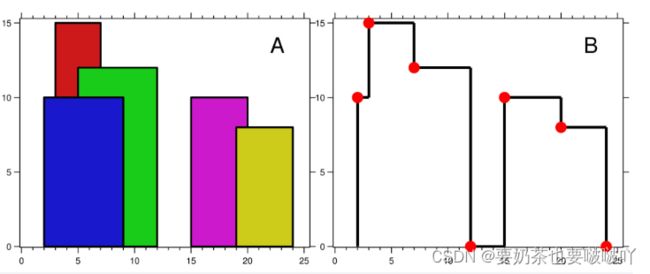
输入：buildings = [[2,9,10],[3,7,15],[5,12,12],[15,20,10],[19,24,8]]
输出：[[2,10],[3,15],[7,12],[12,0],[15,10],[20,8],[24,0]]
解释：
图 A 显示输入的所有建筑物的位置和高度，
图 B 显示由这些建筑物形成的天际线。图 B 中的红点表示输出列表中的关键点。

• 代码实现

class Solution {
    public List<List<Integer>> getSkyline(int[][] buildings) {
        // 如果将所有的建筑的边界作为一条线，那么所有的答案都在这些线上
        // 考虑任意一条线，那么这条线和所有相交的建筑（这里排除掉刚好和建筑右边界相交），取一个最高的
        // 高度，然后判断这个高度是否和ans末尾最后一个元素的高度相等，不相等就加入进去
        // 在这里为了快速得到最高的高度，使用一个堆来进行记录

        // 得到所有由建筑边界构成的边界线，并升序
        int[] boundaries = new int[buildings.length * 2];
        for (int i = 0; i < buildings.length; i++) {
            boundaries[2 * i] = buildings[i][0];
            boundaries[2 * i + 1] = buildings[i][1];
        }
        Arrays.sort(boundaries);

        // 创建一个堆，维护一个边界-高度值对
        PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> b[1] - a[1]);

        List<List<Integer>> ans = new ArrayList<>(); // 返回答案
        int index = 0; // 指向buildings
        for (int boundary : boundaries) {
            // 对于一个建筑，如果其左边界在当前判断的边界线左边或重叠，那么向堆加入右边界-高度值对
            while (index < buildings.length && buildings[index][0] <= boundary) {
                pq.offer(new int[] { buildings[index][1], buildings[index][2] });
                index++;
            }

            // 对于那些加入了堆中的建筑，从堆的顶部移出建筑右边界在边界线左边或重叠的边界-高度值对
            while (!pq.isEmpty() && pq.peek()[0] <= boundary) {
                pq.poll();
            }

            // 经过上面的两步操作之后，当前边界线穿过的建筑（不含右边界）全都在堆中，并且堆的顶端是所有穿过的建筑中，高度最高的，也就是天际线高度
            // 如果此时的堆为空，证明边界线没有穿过任何建筑，来到了建筑的分割位置，天际线为0
            int maxHeight = pq.isEmpty() ? 0 : pq.peek()[1];

            // 按照这种算法，每一条边界线都会产生一个天际线高度，如果这个高度和ans末尾元素的高度一致，那么就说明两条边界线穿过了同一个建筑，并且相邻，那么按照规则只取最左端
            if (ans.size() == 0 || maxHeight != ans.get(ans.size() - 1).get(1)) {
                ans.add(Arrays.asList(boundary, maxHeight));
            }
        }

        return ans;
    }
}