Google Earth Engine(GEE) 多元线性回归拟合 ee.Reducer.linearRegression
在GEE中想要进行多元线性拟合可以使用ee.Reducer.linearRegression方法。这里举个例子,建立温度,降雨,NDVI 与EVI之间的关系。数据时间范围2000-2020。这里我们需要将数据处理为以一个包含21的image的imagecollection,每个image包含四个波段,如上面顺序。此外,如果我们想拟合带有常数的多元线性回归模型时,可以增加一个常数1的波段。
ee.Reducer.linearRegression采用最小二乘方法拟合参数,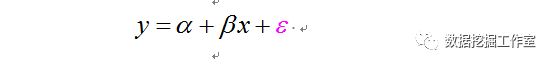
以最小化残差为目标
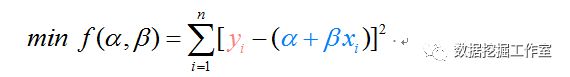
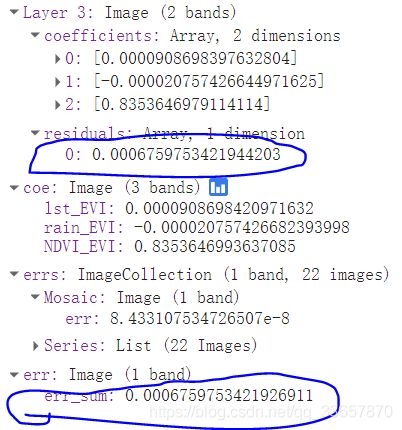
结果返回两个波段,一个是系数,一个是残差(均方根误差)
具体实现如下:
首先将数据处理为imagecollection
var chirps=ee.ImageCollection("UCSB-CHG/CHIRPS/DAILY")
var mod_ndvi=ee.ImageCollection("MODIS/006/MOD13A1")
var mod_lst=ee.ImageCollection("MODIS/006/MOD11A2")
var rain=chirps.filterDate('1981-01-01','1981-12-31')
.reduce(ee.Reducer.sum()).rename('rain').set({'system:time_start':ee.Number(1981)})
var rains=ee.ImageCollection(rain)
print(rains)
var rain_ndvi_lst=ee.ImageCollection(rain)
function ndvi(image)
{
return image.multiply(0.0001)
}
function lst(image)
{
return image.multiply(0.02).subtract(273.15)
}
for (var year=2000;year<2021;year++)
{
var tmp=ee.Image(0)
var t1=ee.String(ee.Number(year)).cat('-01-01')
var t2=ee.String(ee.Number(year)).cat('-12-31')
var rain_tmp=chirps.filterDate(t1,t2)
.reduce(ee.Reducer.sum()).rename('rain')//.set({'system:time_start':ee.Number(year)})
var ndvi_tmp=mod_ndvi.filterDate(t1,t2).select(['NDVI','EVI'])
.reduce(ee.Reducer.max()).rename(['NDVI','EVI']).multiply(0.0001)
var lst_tmp=mod_lst.filterDate(t1,t2).select('LST_Day_1km')
.reduce(ee.Reducer.max()).rename('lst').multiply(0.02).subtract(273.15)
tmp=tmp.addBands(lst_tmp).addBands(rain_tmp).addBands(ndvi_tmp).slice(1)
//print(tmp)
rains=rains.merge(rain_tmp)
rain_ndvi_lst= rain_ndvi_lst.merge(tmp)
}
print(rains)
rain_ndvi_lst=rain_ndvi_lst.filter(ee.Filter.eq('system:time_start',1981).not())
print(rain_ndvi_lst,'rain_ndvi_lst')
然后将ee.Reducer.linearRegression拟合参数,
var linearRegression = rain_ndvi_lst.reduce(
ee.Reducer.linearRegression({
numX: 3,
numY: 1
}));
为了验证残差是否为均方根误差,我们用拟合的参数反算均方根误差,
var name1='lst'
var name2='rain'
var name3='NDVI'
var name4='EVI'
var bandNames =[ [name1, name2,name3] ,[name4]]// 0-axis variation.
var coe=linearRegression.select('coefficients').arrayFlatten(bandNames)
print(coe,'coe')
Map.addLayer(coe,{},'coe')
var list=rain_ndvi_lst.toList(rain_ndvi_lst.size())
var num=rain_ndvi_lst.size().getInfo()
var errs=ee.ImageCollection(ee.Image(0).rename('err').toDouble())
for (var i=0;i整体代码如下
var chirps=ee.ImageCollection("UCSB-CHG/CHIRPS/DAILY")
var mod_ndvi=ee.ImageCollection("MODIS/006/MOD13A1")
var mod_lst=ee.ImageCollection("MODIS/006/MOD11A2")
var rain=chirps.filterDate('1981-01-01','1981-12-31')
.reduce(ee.Reducer.sum()).rename('rain').set({'system:time_start':ee.Number(1981)})
var rains=ee.ImageCollection(rain)
print(rains)
var rain_ndvi_lst=ee.ImageCollection(rain)
function ndvi(image)
{
return image.multiply(0.0001)
}
function lst(image)
{
return image.multiply(0.02).subtract(273.15)
}
for (var year=2000;year<2021;year++)
{
var tmp=ee.Image(0)
var t1=ee.String(ee.Number(year)).cat('-01-01')
var t2=ee.String(ee.Number(year)).cat('-12-31')
var rain_tmp=chirps.filterDate(t1,t2)
.reduce(ee.Reducer.sum()).rename('rain')//.set({'system:time_start':ee.Number(year)})
var ndvi_tmp=mod_ndvi.filterDate(t1,t2).select(['NDVI','EVI'])
.reduce(ee.Reducer.max()).rename(['NDVI','EVI']).multiply(0.0001)
var lst_tmp=mod_lst.filterDate(t1,t2).select('LST_Day_1km')
.reduce(ee.Reducer.max()).rename('lst').multiply(0.02).subtract(273.15)
tmp=tmp.addBands(lst_tmp).addBands(rain_tmp).addBands(ndvi_tmp).slice(1)
//print(tmp)
rains=rains.merge(rain_tmp)
rain_ndvi_lst= rain_ndvi_lst.merge(tmp)
}
print(rains)
rain_ndvi_lst=rain_ndvi_lst.filter(ee.Filter.eq('system:time_start',1981).not())
print(rain_ndvi_lst,'rain_ndvi_lst')
var ccdc=ee.Algorithms.TemporalSegmentation.Ccdc(rain_ndvi_lst, ['rain'])
print(ccdc)
Map.addLayer(rains)
Map.addLayer(ccdc)
var linearRegression = rain_ndvi_lst.reduce(
ee.Reducer.linearRegression({
numX: 3,
numY: 1
}));
print(linearRegression)
Map.addLayer(linearRegression)
var name1='lst'
var name2='rain'
var name3='NDVI'
var name4='EVI'
var bandNames =[ [name1, name2,name3] ,[name4]]// 0-axis variation.
var coe=linearRegression.select('coefficients').arrayFlatten(bandNames)
print(coe,'coe')
Map.addLayer(coe,{},'coe')
var list=rain_ndvi_lst.toList(rain_ndvi_lst.size())
var num=rain_ndvi_lst.size().getInfo()
var errs=ee.ImageCollection(ee.Image(0).rename('err').toDouble())
for (var i=0;i