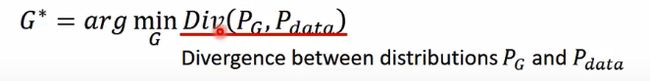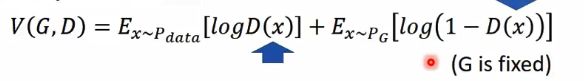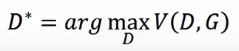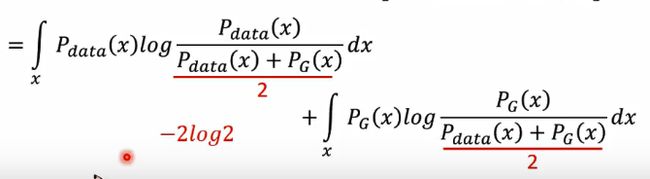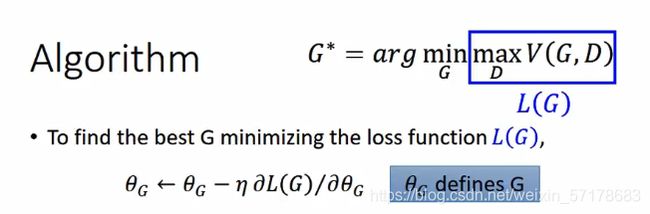李宏毅机器学习33——GAN（5）

摘要：

这节课主要学习了GAN背后的理论知识，主要是原理和数学推导。

由于GAN是两部分组成的，这节课学习也是分为生成器生成图片的原理与判别器的原理。

对生成器而言，想要生成符合要求目标，需要在高维空间中选取出样本的分布情况。将选取的样本通过生成器，得到Pg。希望Pg与目标样本Pdata尽可能接近，这个过程其实就是求这两个分布的KL散度。

对于判别器而言，虽然不知道两个分布的具体公式，但是通过分别sample出两个数据集，对其进行分数评估，得到目标函数。

之后将判别器与生成器的目标函数联系起来，就是GAN的目标函数。

对于整体的目标函数，理论方法进行了一些假设，与实际情况还略有不同。

目录

一、GAN背后的理论

二、极大似然估计

三、generator

四、discrimination

五、整理公式

算法过程：

实际做法：

算法总结：

总结：

---

Theory behind GAN

一、GAN背后的理论

对抗网络GAN是由生成器Generator最终生成图片、文本等结构化数据。

生成器能生成结构化数据的原理是什么呢？

假设今天的任务是生成固定的图片，实际上我们是在一个已知的image space中，选出分布Pdata（x），在这个分布中的图片都是符合我们选取要求的。

二、极大似然估计

在GAN之前，我们采取极大似然估计的方法，去找到这个分布Pdata（x）

极大似然估计的做法：

1.我们首先有目标数据的概率密度函数Pdata（x）

我们只能从Pdata（x）中sample。

2.我们设定Generator的概率密度函数为Pg（x；θ）

假设Pg是高斯分布，θ代表高斯分布的均值和方差，我们希望通过调整参数θ，是Pg与Pdata（x）尽可能接近。

3.从 Pdata（x）中sample样本x1，x2，，，xm。然后我们计算每个样本中Pg的值。

4.对这m个Pg的概率进行相乘，通过调整参θ，让L最大。

极大似然函数的推导过程

KL散度（KL divergence）就是衡量两个分布的差异性的公式，越小差异性越小。当然也可以用其他计算差异性的公式来计算。

通过一系列的推导，得出极大似然估计=最小KL散度

所有机器学习中的最大似然估计，其实就是最小化我们要寻找的目标分布Pg和Pdata的KL散度。

那么现在的问题就是如何定义Pg

三、generator

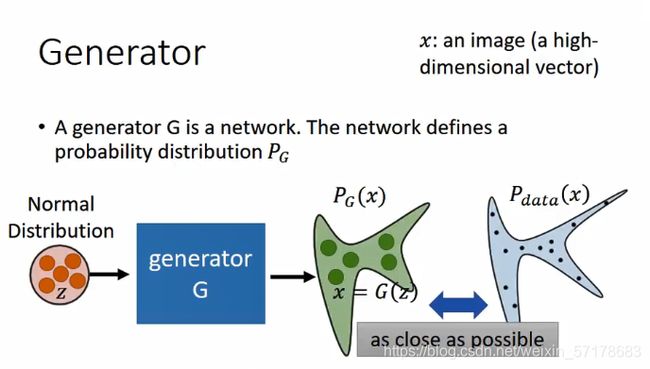
生成器G是一个网络，它定义了一个可能的分布Pg

每次从normal distribution中选出一个z，丢给生成器，产生一个x。最终产生出x的集合，就是另外一个distribution。而我们的目标就是让这两个distribution越接近越好。

这就用到上面的推导结论：计算Pg和Pdata，让它们的散度越小越好。

目前我们不知道Pg和Pdata的公式，这就需要用到判别器了。

四、discrimination

虽然我们不知道Pg和Pdata的公式，但是sample出一些样本，对于Pdata来说，我们之间从数据集中进行sample，对于Pg来说，我们可以按照上图的方法，通过generator进行sample。

有了这两个sample的数据集，通过判别器就可以计算了。

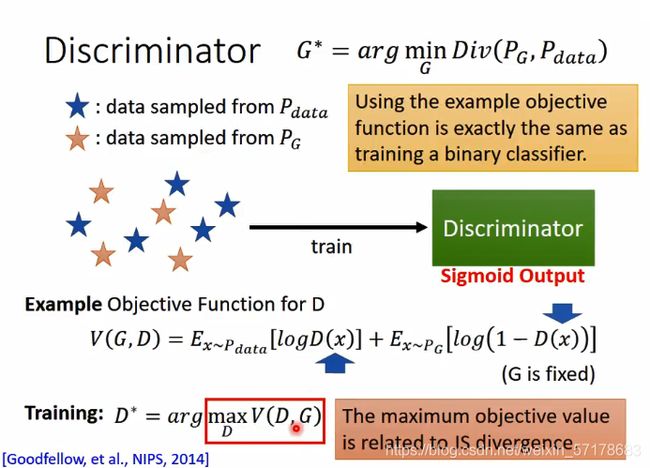
判别器的目标函数：

这个目标函数的意思是，假设x是从Pdata里面sample出来的的，那么希望logD（x）越大越好：假设x是从Pg中sample出来的，就希望它的值越小越好。

训练的时候就是用函数D，来max V（G，D）

这个公式其实和逻辑回归的二分类目标函数是一样的，将两个sample集合看做是两个分类，训练Discriminator就好比训练一个二分类。

训练到最后发现得到的D，其实就是JS divergence

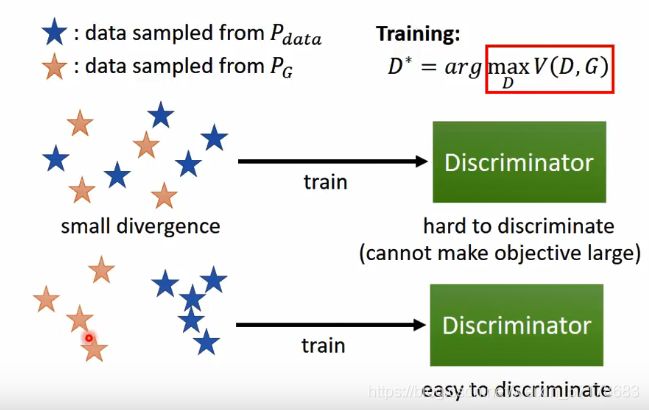
将整个流程理解成二分类，那么当两个类别很紧密时，判别器很难区别这两个类别的不同。这样训练下去，二分类的目标函数loss很难被压低。回过头来，这也就意味着很难找到一个D，让V(D,G)变得很大。这意味着这两堆data，它们是非常接近的，也就是small divergence。

数学推导：

对V（G,D）进行整理，这里要注意有一个假设D(x)可以为任意函数。

（实际上只有network无限大才能达到这个要求）

对D(X)求微分，得到D(X)的值,之后将得到的值带入到原式中，整理。在D(X) 项的分子分母同时成1/2，又将分子中的1/2提出，得到-2log2。

这是最后一步的变换公式：

Pg和Pdata越远，后两项和越大。

总结判别器这部分：

当我们在训练一个判别器的时候，就是在评估从Pg和Pdata中sample出两个数据集，它们之间的JS divergence。（也就是相似程度）

五、整理公式

原本生成式目标函数中Div（Pg，Pdata）由于不知道Pg和Pdata是无法计算的。

但是通过判别式目标函数，经过上面一系列的计算，求出maxD*，这个D*其实就是Div（Pg，Pdata）。之后我们将这部分替换掉。

将

变成：

模拟G*的求解过程：（假设只有三个不同的G）

横坐标变换代表选择不同的判别器

首先，先看每个G中V（G,D）最大的值

然后，在这三个点，选择一个G，可以最小化这个V（G,D）

所以最后选择了G3

这里绿线的高度表示Pg和Pdata之间的divergence

接下来就是求解G*的过程了、

之前将GAN的训练方法，一般分成两部分：

第一步是初始化生成器和判别器。

第二步是先固定生成器，去训练判别器，然后固定判别器，去训练生成器，这个过程要重复多次。

算法过程：

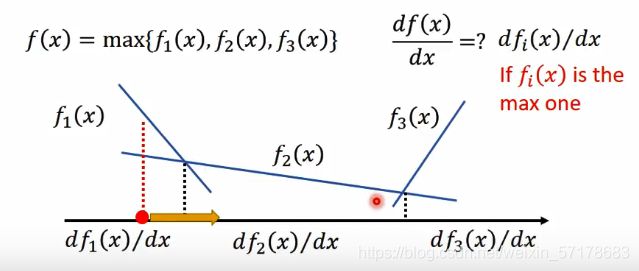
先将maxV（G,D）取出来，用L（G）表示，对G求微分。（假设D（x）已知，看做常量）

对于max函数如何求微分，李老师还拿了分段函数进行具体举例

一开始有初始的G0，计算L（G）对G的微分。

先找到让V最大的D0*。（这个过程可以使用梯度上升）

微分，更新参数，得到新的G1。

再找到让V最大的D1*。

微分，更新参数，得到新的G2

……

实际做法：

实际上在做GAN的时候，是没法算Ex的，所以都是sample代替的，我们分别将Pdata和Pg中 sample的数据丢给D，计算出分数求平均值，求得V的均值，这个过程其实就是在训练一个二分类的模型。

算法总结：

将整个算法总结起来：也就是第一节课看到的表

总结：

在没有GAN之前，一般用极大似然估计来进行生成，但是极大似然估计有其局限性，当函数比较简单时，就没办法很好的解决问题，当函数太过复杂，可能无法求解。于是便有了生成器，用神经网络作为函数，理论上来说，如果神经网络足够大，就可以构成所有的函数，而其求解时可以用优化方法自动求解，很好的突破了极大似然估计的局限性。在训练时，我们还需要一个判别器，用来对生成数据与训练数据进行比较，判别器主要是衡量生成数据和训练数据的差距，再反馈给生成器，生成器知道差距后就去缩小差距，完善后再次将生成数据丢给判别器，这样循环往复，直至找到合适的生成器，这就是GAN的全部流程。