第十五次作业 马尔科夫链

物联202   邱郑思毓  2008070213

作业要求：学习马尔科夫链的相关内容，编程展示马尔科夫链的原理和结果。

完成情况：

概念：它假设某一时刻状态转移的概率只依赖于它的前一个状态。

式子只与前一个式子有关，和之前的式子没有关系。

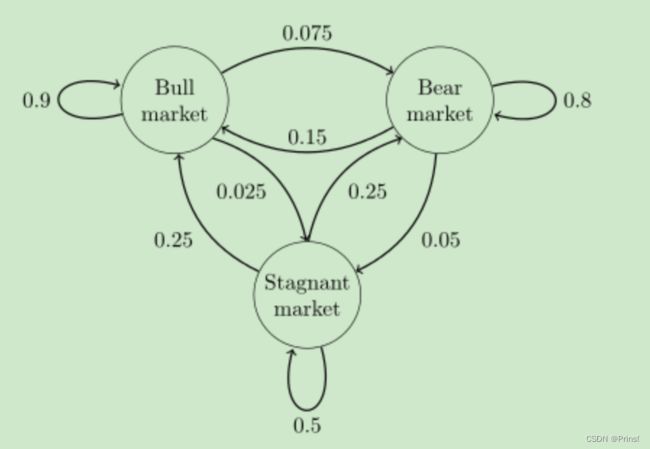
这个马尔科夫链是表示股市模型的，共有三种状态：牛市（Bull market）, 熊市（Bear market）和横盘（Stagnant market）。每一个状态都以一定的概率转化到下一个状态。 

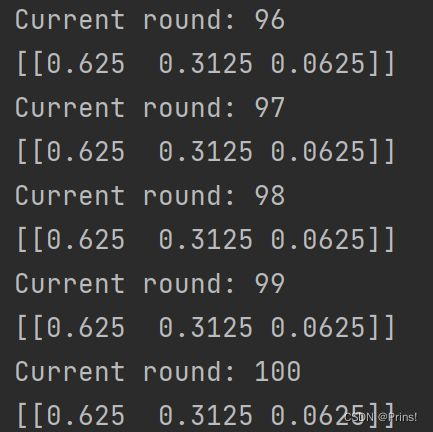
        无论出事概率分布如何，最概率都会趋近于（0.625,0.3125,0.0625）。也就是说我们的马尔科夫链模型的状态转移矩阵收敛到的稳定概率分布与我们的初始状态概率分布无关。这是一个非常好的性质，也就是说，如果我们得到了这个稳定概率分布对应的马尔科夫链模型的状态转移矩阵，则我们可以用任意的概率分布样本开始，带入马尔科夫链模型的状态转移矩阵，这样经过一些序列的转换，最终就可以得到符合对应稳定概率分布的样本。

代码实现：

import numpy as np

#设定各个转换的概率
a=np.array([[0.9,0.075,0.025],[0.15,0.8,0.05],[0.25,0.25,0.5]],dtype=float)
#设定初始的概率为 牛：0.7 熊：0.1 横：0.2
v=np.array([[0.7,0.1,0.2]],dtype=float)
#进行100个轮回
for i in range(100):
    #计算每一次出现各个盘的概率
    v = np.dot(v,a)
    print("Current round:" , i+1)
    print (v)

结果为：

 

当初始的概率设定为0.3,0.4,0.3时，代码如下：

import numpy as np

#设定各个转换的概率
a=np.array([[0.9,0.075,0.025],[0.15,0.8,0.05],[0.25,0.25,0.5]],dtype=float)
#设定初始的概率为 牛：0.3 熊：0.4 横：0.3
v=np.array([[0.3,0.4,0.3]],dtype=float)
#进行100个轮回
for i in range(100):
    #计算每一次出现各个盘的概率
    v = np.dot(v,a)
    print("Current round:" , i+1)
    print (v)

结果和上边的是一样的。